改进BP神经网络的空地制导弹药打击目标价值评估

吴 鹏，诸德放，刘子易

（1.空军勤务学院，江苏 徐州 221000；2.解放军94865部队，杭州 310000）

0 引言

目标价值是指战场目标打击价值，用来描述和衡量在一定战斗条件下，对战场目标实施打击必要性的一个综合性指标[1]，目标价值评估即量化分析目标价值。空地制导弹药作为高价值、大威力武器，合理安排其打击目标具有重要意义。目前，我军对炮兵打击目标价值的研究较多，很少涉及空地制导弹药打击目标，且多采用层次分析法、多属性决策法或模糊分析法进行分析，此类方法处理特征信息的方式粗糙，误差较大。BP神经网络具有储存和应用经验知识的自然特性，自学习能力强，善于联想、概括、类比和推广，将BP神经网络应用于目标价值评估具有良好的前景。同时，BP神经网络的缺点也很明显，网络的泛化能力差、容易陷入局部最小值，因此，需要对网络进行改进才能保证评估效果。

本文提出了一种改进BP神经网络，使用贝叶斯正则化方法和遗传算法优化BP神经网络。结论表明，该方法有效改善了网络的性能，保证了预测精度。

1 目标价值评估指标体系

目标价值评估指标的选取直接影响着评估结论的准确性和客观性。选取指标时，要充分考虑空地制导弹药性能特点、作战任务规划和目标属性。

空地制导弹药打击目标的过程可描述为3个阶段：突防阶段、制导阶段和末端打击阶段。突防阶段，弹药突破敌方电磁干扰、地导高炮反击等手段的封锁，受目标的反击能力的影响；制导阶段，弹药通过制导系统导引抵达目标上空并锁定目标，受目标伪装程度、信息可靠程度等因素影响；末端打击阶段，弹药抵达目标并通过战斗部毁伤目标，受弹药毁伤特性、目标易毁性等因素影响。只有顺利完成3个阶段的任务，制导弹药才能充分发挥自身的毁伤特性。综合考虑打击的3个阶段和作战任务规划，并结合相关文献，选取如下目标价值评估指标：

1）任务一致性：指目标对主要作战行动的影响程度[2]，体现在对我方战术目标的影响和对敌方企图的影响两方面。与主要作战任务方向越一致，目标价值越大。

2）打击紧迫性：指对目标进行打击的时限要求。体现在目标对我方部队产生危害所需时间和不对目标进行射击目标逃匿的可能性两个方面，由目标所处状态和机动性两个因素决定[3]。对目标进行打击的紧迫程度越高，目标价值越大。

3）信息可靠性：指目标信息的可靠程度。体现在情报信息的准确性和目标的伪装程度两个方面，情报越准确、伪装程度越低，目标信息越可靠。信息可靠性越高，目标价值越大。

4）目标威胁性：指目标火力强弱和作战企图对我方载机、指挥机构乃至整个作战意图构成威胁的大小。威胁程度越大，目标价值越高。

5）目标反击能力：指目标对弹药打击的抗击强度以及可能对我造成的火力损伤程度[4]。主要体现在目标对弹药进行封锁和干扰的能力。目标反击能力越高，价值越高。

6）目标易毁性：指受到相同程度的打击后目标的毁伤程度。体现在目标被摧毁的难易程度和快速恢复能力两个方面[5-6]。易毁性越高，目标价值越大。

这6个指标构成了目标价值的特征集，通过对6个指标赋分，可完成对目标价值的基本描述。

2 改进BP神经网络模型

2.1 BP神经网络

BP神经网络是指基于误差反向传播算法的多层前向神经网络，由输入层、输出层和若干个隐含层组成，一个3输入2输出的三层BP网络结构如图1所示。

图1 3输入2输出的三层BP网络结构

其学习过程可以描述为两个过程：1）工作信号的正向传播：输入信号从输入层经隐单元，传向输出层，在输出端输出产生输出信号。2）误差信号反向传播：网络的实际输出与期望输出之间的差值即为误差信号，误差信号由输入端开始逐层向前传播。当误差小于设定值、权值的变化很小或达到最大迭代次数时，学习停止，神经网络训练完成。

由于选取了6个评价指标，故本模型采用6输入1输出的BP网络结构。

2.2 贝叶斯正则化BP神经网络

传统的BP神经网络一般采用LM算法，将网络的训练误差平方和作为性能函数，该算法的泛化能力较差。故采用贝叶斯正则化方法对BP网络进行改进，将神经网络权值和阈值的均方差引入性能函数，通过正则化系数的调整使小作用的连接权趋于零，在保证网络精度的前提下，剪除冗余的连接权和神经元，从而提高网络的泛化能力[7]。

改进后的性能函数如下：

网络中的权值修正如下：

式中：E为修正后的性能函数，EW为权衰减项，ED为误差函数，α，β为正则化系数，n为样本数量，m为权值和阈值的数量，yi为第i个样本的实际输出，ti为第i个样本的期望输出，ωj为第j个权值（包含阈值），η为学习步长，vi为前一层的输出。

贝叶斯正则化方法中，正则化系数决定着神经网络的训练目标，α＜＜β时，重点训练误差函数，可能出现过拟合现象；α＞＞β时，重点训练权衰减项，可能出现误差较大的问题[8]。因此，正则化系数的确定十分关键。该方法将系数设为随机变量，系数的概率密度最大时即为最优正则化系数，最优解为：

式中：WP为E取最小值时所对应的权值（包含阈值）矩阵，γ为有效参数个数，为E在WP处的海森矩阵。

2.3 遗传算法

遗传算法是一种借鉴生物界自然选择和基因分离组合定律的全局优化搜索算法。遗传算法对参数的编码从多点进行操作，可以有效防止搜索过程陷于局部最优解。BP网络沿着误差减小的最大梯度方向调整网络权值，容易陷入局部最小值，采用遗传算法优化BP网络的初始权值，可以有效改善此问题，优化步骤如下[9]：

1）对BP神经网络的初始权值和阈值进行随机种群初始化实数编码；

2）计算种群适应度，寻找最优个体；将误差函数绝对值作为适应度函数F：

其中y为样本的预测值，t为样本的实际值。

3）进行遗传算子操作（选择、交叉、变异），产生新一代个体。

选择操作选用基于适应度比例的轮盘赌法，个体i的选择概率为pi：

交叉操作采用实数交叉法，第k个染色体ak和第l个染色体al在j位的交叉操作方法如下：

第i个染色体的第j个基因的变异操作方法如下：

其中 N 为种群数，b、r为[0，1]间的随机数，amax为基因aij的上界，amin为基因aij的上界，r2为一个随机数，g为当前迭代次数，Gmax为最大进化次数[10]。

4）判断进化是否结束，若是，则输出最优解，若否，则返回2）继续操作。

5）对最优个体解码，确定BP网络的最优权值和阈值。

使用贝叶斯正则化方法和遗传算法优化BP神经网络具体流程如图2所示：

图2 贝叶斯正则化方法和遗传算法优化BP神经网络流程

2.4 BP神经网络与遗传算法参数设置

根据Kolmogorow定理，一个三层的BP神经网络能够逼近任意复杂的非线性映射，故采用三层BP神经网络。BP神经网络隐层数的确定没有具体的理论依据，可按公式来确定，n为输入单元数，m为输出神经元数，k为[1，10]之间的常数。经过多次测试，当k取6时，取得最佳预测精度，故隐含层取9个节点。BP神经网络的参数设置如下页表1所示。

遗传算法的参数设置如下页表2所示。

3 实例分析

3.1 训练样本的选取

训练样本的质量直接决定着网络评估结果的准确性，选择样本数据时应当注意样本的代表性和数据的准确性。假定我方遂行登岛作战任务，计划使用空地制导弹药对敌进行打击，天气状况良好，弹药性能正常。在此背景下，将专家评定的12类典型目标的经验数据作为样本，标准化处理后，数据如表3所示，其中X1～X6为前述6个指标得分，Y为目标经验价值。

表1 BP神经网络参数设置

表2 遗传算法参数设置

表3 典型目标的指标经验数据

3.2 仿真结果

利用MATLAB软件建立上文所述的改进BP神经网络模型，将前9组数据用于训练，达到设定的精度要求后，利用后3组数据对网络进行测试，测试结果与主成分分析法[11]和传统BP网络模型计算结果进行对比。4种模型的仿真结果如表4所示。

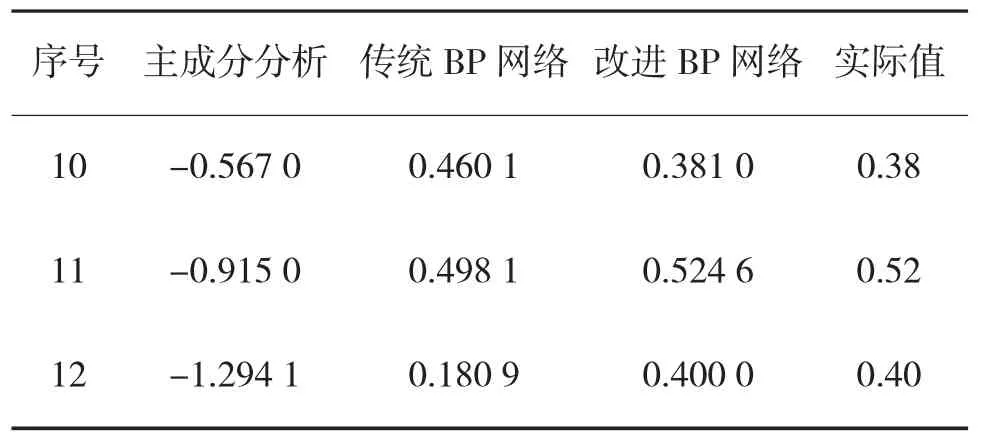
表4 4种模型测试结果

两种BP网络评估结果与实际值的拟合曲线如图3所示。

3种模型评估结果的误差曲线如图4所示。

图3 两种BP网络评估结果与实际值拟合曲线

图4 3种模型评估结果误差曲线

由图3、图4可见，经过贝叶斯正则化方法和遗传算法优化的BP神经网络预测值与实际值误差最小，较改进之前泛化能力更佳，建模精度优越。

4 结论

空地制导弹药作为我空军实施空中精确打击的重要手段，研究其打击目标价值，对于提高其作战效能，具有重要的现实意义和军事价值。本文结合空地制导弹药性能特点、作战任务规划和目标属性，选取了6个目标价值评估指标。此外，利用贝叶斯正则化方法和遗传算法优化BP神经网络，建立了目标价值评估模型，测试结果表明，优化后模型性能优异，在空地弹药打击目标价值评估中具有实用意义，能够为指挥机关决策提供依据或参考。