基于卷积神经网络的图像编辑传播

,,

(浙江工业大学 理学院,浙江 杭州 310023)

随着数字多媒体硬件的发展和软件技术的兴起,图像色彩处理的需求不断增长,在显示设备上进行快速高效的图像色彩处理变得尤其重要。编辑传播作为一种快速的图像色彩处理的方法,是指用户通过交互的方式,对图像中不同的物体给予不同的颜色笔触,然后进行特征提取和识别,实现图像编辑处理的过程。目前,基于单幅图像的编辑传播算法有很多,早期Levin等[1]通过对相邻像素构造稀疏相关矩阵将该问题转换为一个优化问题,实现了图像编辑传播,但是在处理片段的图像区域时,需要更多的笔触才能达到满意的效果,于是An等[2]引入了基于像素对的约束,使得图像编辑传播更直观,更易于控制。之后Xu等[3]使用了基于KD树的聚类,简化了编辑传播的优化问题,同时也加快了图像编辑传播的速度.2012年,Chen等[4]受到局部线性嵌入方法的启发,在特征空间上建立流行结构,并通过保持这种流行结构来实现编辑传播。此后,Chen等[5]又使用字典学习的方法,加快了基于流行学习实现编辑传播的方式。在编辑传播过程中,往往隐式的要求笔触合理,为了减少对笔触的依赖,Xu等[6]考虑了空间位置,样本位置和视觉外观,自动地确定样本在整个图像中的影响。这些方法在提取图像特征时,不同图像的关键特征不尽相同,不易于泛化。此外一些精心设计的特征,对特定的问题比较有效,但是往往容易局限于设计者的考虑,并且需要较多的领域知识,如灰度行程纹理特征[7]等。Endo等[8]提出使用卷积神经网络对笔触覆盖的像素点提取特征,根据提取到的特征将不同的像素点染为不同的颜色,从而将该问题转换为一个分类问题。然而当使用卷积提取特征时,也意味着假定了模型的变换是固定的,这样先验知识不利于模型的泛化。

对于图像编辑传播问题,笔者提出使用组合卷积来提取笔触覆盖的像素点的特征,并结合有偏的损失函数,构建了一个双分支的卷积神经网络模型。组合卷积对进行卷积操作的元素进行随机地偏移,可以使得模型的接受视野更加合理,泛化能力更强。同时,组合卷积可以减少模型的中参数量和操作数,降低模型的复杂度,加快图像编辑传播的速度。使用该双分支的卷积神经网络模型,可以实现图像的有效上色,并在一定程度上改善编辑传播过程中颜色溢出的情况,取得较好的视觉效果。

1 研究背景

1.1 卷积神经网络

20世纪60年代,Hubel和Wiesel在研究猫和猴子的视觉皮层时,发现他们用于感知局部视觉区域的神经元拥有独特的网络结构,该结构可以有效地降低反馈神经网络的复杂性.1980年,Fukushima第1次提出了一个基于感受野的理论模型Neocognitron[9].20世纪90年代,一些研究者提出了卷积神经网络这个概念,并在手写数字识别中取得了良好的识别效果[10-11].2012年,在ImageNet大规模视觉识别挑战赛中,深度卷积神经网络取得了第1名的成绩[12]。这证明了卷积神经网络在复杂模型下的有效性,同时也大大推动了深度神经网络的发展。近年来,神经网络越来越受到研究者们的重视,在多个领域中都取得了较好的成绩。同时,神经网络也开始逐渐应用到了人们的生活和工业中,如使用神经网络进行深基坑维护形变预测[13]和工件识别[14]。卷积神经网络是人工神经网络的一种,典型的用于分类的卷积神经网络由输入层、卷积层、池化层、全连接层及输出层组成,大致结构如图1所示。

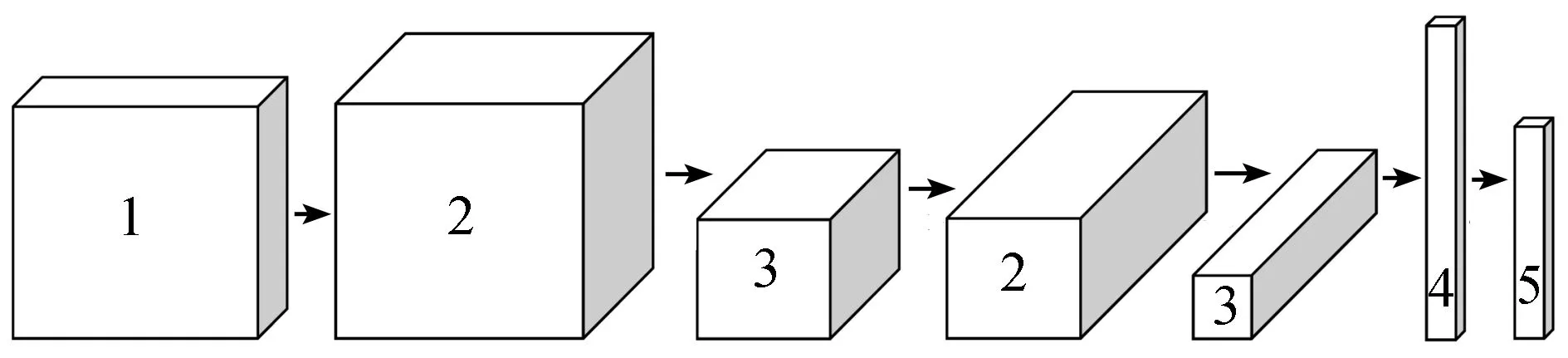
1—输入层;2—卷积层;3—池化层;4—全连接层;5—输出层图1 典型的卷神经网络Fig.1 Classical convolutional neural network

卷积层由多个特征面组成,每个特征面由多个神经元组成,它的每一个神经元通过卷积核与上一层特征面的局部区域相连。卷积核是一个权值矩。卷积神经网络通过卷积操作提取输入的不同特征。浅层的卷积层提取低层次的特征,例如物体边缘、角点和纹理等。深层的卷积层则提取更高级的特征。

神经网络模型另一个很重要的方面是设计损失函数。输出层与损失函数紧密相连,输出的形式往往决定了损失函数的形式。对于n分类问题,常常使用softmax函数来得到这n个类别的一个概率分布p(y|x;θ)。对于模型预测得到的概率分布q(y|x;θ),一般使用交叉熵作为损失函数,用来衡量训练数据和模型的预测之间的相似性。

1.2 编辑传播

编辑传播主要分为两步:第1步首先通过用户交互的方式给予图像中的物体一些带颜色笔触;第2步根据像素点之间的相似性,将笔触的颜色传递到其他相似的像素点。如图2所示,图2(b)是在羊上添加了颜色笔触后的笔触图,其中黑色的笔触表示背景,在处理过程中要求不改变背景的颜色。图2(d)是根据笔触信息实现编辑传播后的效果图。

图2 实验对比Fig.2 Experimental comparison

假设在图像中指定n种颜色的笔触,那么对于任一笔触覆盖的像素点,可以提取该像素点的邻域像素块p和位置坐标s。Endo等[8]使用了两个卷积层对p提取视觉特征fv,使用全连接层对s提取空间位置特征fs,即

fv=Gv(p;θv)

(1)

fs=Gs(s;θs)

(2)

式中:Gv为两个卷积层的函数表示;Gs为全连接层的函数表示;θv为两个卷积层中的参数;θs为全连接层中的参数。根据式(1,2),将特征fv和fs融合,得到特征fc为

fc=Gc(fv,fs;θc)

(3)

式中:Gc为全连接层的函数表示;θc为该全连接层中的参数。根据融合后的特征fc进行分类,得到概率向量y为

y=Gl(fc;θl)

(4)

式中:Gl为softmax函数;θl为参数。概率向量中的任一分量yi∈[0,1]表示该像素属于第i种颜色的概率。这样就将编辑传播问题转换为了一个分类问题,实验结果如图2(c)所示。

典型的卷积神经网络使用卷积操作来提取图像中的特征,但是一旦选择了使用卷积来提取特征也就决定了模型对输入的变换,这样固定的变换不利于模型的泛化。并且典型的卷积包含了较多的参数量和操作数,模型的复杂度较高。而在基于稀疏的笔触进行编辑传播的过程中,模型的训练样本较少,不需要特别复杂的模型。同时测试样本相对较多,模型又需要有更好的泛化能力。为了增强泛化能力,减少模型的复杂度,笔者引入了组合卷积。

2 组合卷积

组合卷积由可变形卷积[15]和可分离卷积组成,如图3所示。可变形的卷积可以提取更合理的特征,增强模型的泛化能力;可分离卷积可以减少模型的参数量和操作数,降低模型的复杂度。

图3 组合卷积Fig.3 Combinational convolution

2.1 可变形卷积

典型的卷积操作一般分为两步,首先在输入特征图x上取一个正方形的区域R,再将区域R中的值分别与权重矩阵w中相应位置的值相乘并求和。我们假设R为一个3×3的区域,中心位置的坐标设为(0,0),那么区域R中的元素的坐标为

R={(-1,-1),(-1,0),…,(0,1),(1,1)}

(5)

那么对于图像上任一像素点i,经过卷积操作可以得到输出的值f(i)为

(6)

式中in表示相对于像素点i的位置偏移。

可变形卷积在典型卷积的基础上,对区域R中每一个元素进行了不同程度的偏移,如图4所示。像素点i+in的偏移量用{Δin|n=1,…,N}表示,这里的N=|R|,表示区域R中元素的个数。因此式(6)可以表达为

(7)

式中:Δin为一个二维向量;i+in+Δin表示任意的非整数位置。Δin数值为浮点型,表示在x坐标和y坐标上的偏移量。然而偏移后的坐标值为浮点型,这里不能根据浮点型的坐标值得到对应的像素值,因此在实现时采用的是双线性插值。在实现过程中,对于任意输入特征图,Dai等[15]使用卷积操作得到输出特征图x,x表示偏移后的坐标位置,然后根据偏移后的位置进行双线性插值,得到偏移后的位置对应的像素值。其可以表达为

(8)

式中:i遍历整个特征图x;G(·,·)则表示一个双线性插值的操作。

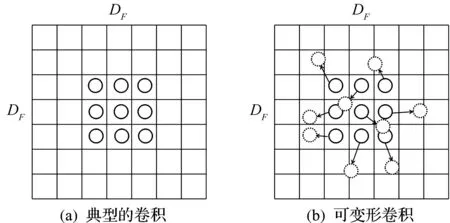
图4 典型的卷积和可变形卷积Fig.4 Classical convolution and deformable convolution

2.2 可分离卷积

对于编辑传播的问题,训练集一般较少。对于小数据集的训练,模型的复杂度过高容易导致过拟合。使用可分离卷积可以减少模型的参数量,降低模型的复杂度,并加快了模型的训练。

假设卷积层的输入特征图的大小为DF×DF×M,DF为特征图的宽和高,M为特征图的数量;卷积核的大小为DK×DK×N,DK为卷积核的大小,N为卷积核的数量。同时假设卷积操作不改变输入特征图的宽和高,那么典型的卷积操作得到的输出为DF×DF×N。对于典型的卷积,整个操作需要的参数量为DK×DK×N×M,同时该操作所需的乘法操作数量为DK×DK×N×M×DF×DF。

可分离卷积将上述卷积操作分成滤波和融合两部分,如图5所示。滤波操作对输入特征图的每一个通道使用一个卷积核,也即使用M个DK×DK的卷积核。经过滤波操作可以得到输出的大小为DF×DF×M,这里的参数量为DK×DK×M,所需的乘法操作数量为DF×DF×M×DK×DK。融合操作是对第一步滤波操作之后的结果进行逐点卷积。融合操作对输入的M个DF×DF特征图,使用N个的卷积核,得到最后的输出大小为DF×DF×N。融合操作中含有N个参数,所需的乘法操作数量为DK×DK×N×M。可分离卷积共包含DF×DF×M+N个参数,以及所需的乘法操作数量为DF×DF×M×DK×DK+DF×DF×N×M。

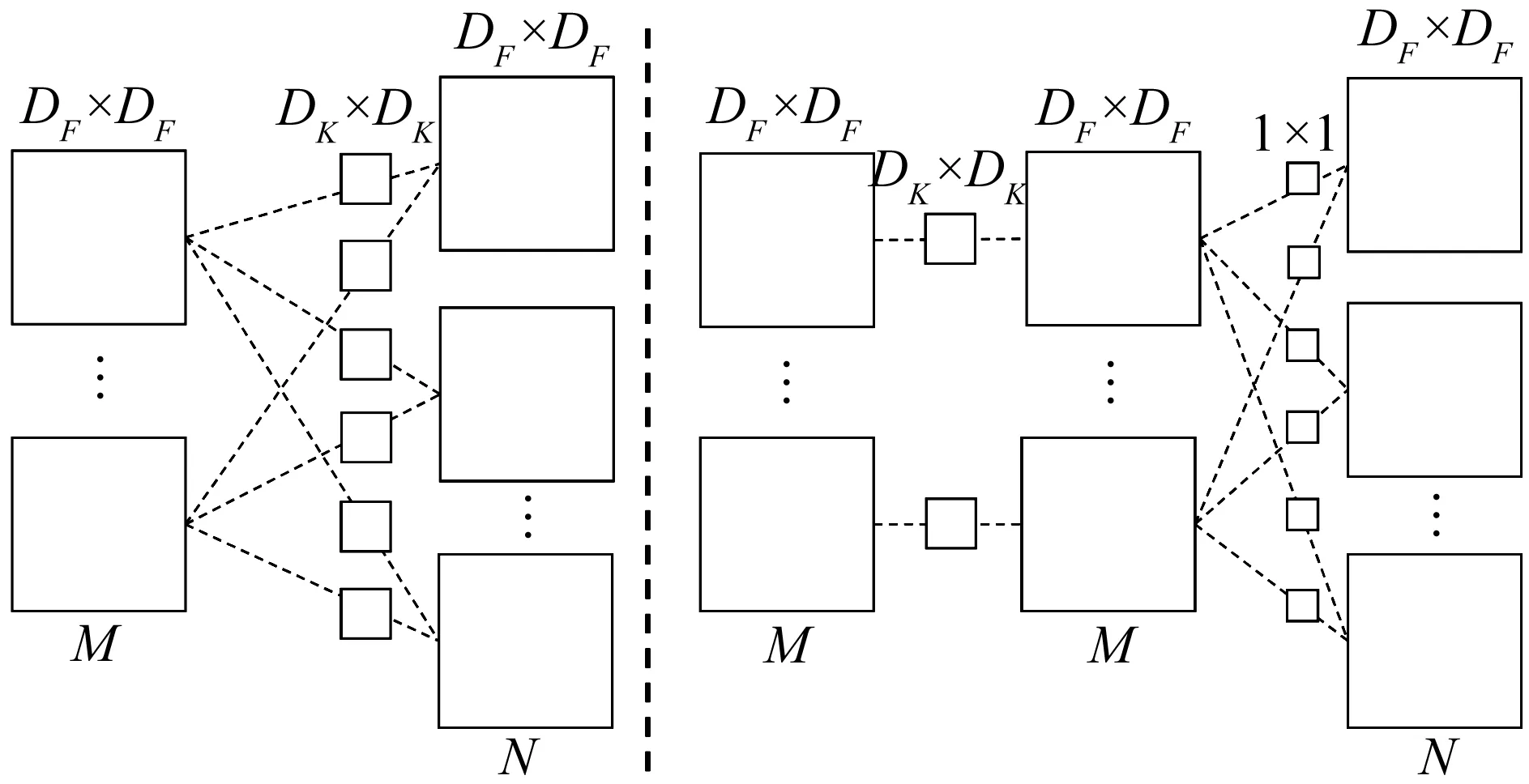
图5 典型的卷积和可分离卷积 Fig.5 Classical convolution and depthwise separable convolution

通过比较,可以得到可分离卷积与典型卷积的参数量之比为

(9)

乘法操作数量之比为

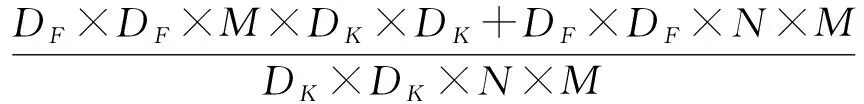
(10)

如果输入的特征图为3通道,并且使用3×3×64的卷积核,那么可分离卷积可以将参数量减少为典型卷积的1/20左右,计算量减少为典型卷积的1/9左右。

3 损失函数与模型结构

3.1 有偏损失函数

在图像编辑传播的过程中,黑色笔触覆盖的像素点被认为是背景类,在处理过程中要求不改变其原有的颜色。对于一幅待处理的图像,目标是希望与背景类相似度较高的像素点也不改变原有的颜色。然而在处理过程中,由于没有强制的边界约束,靠近物体且与背景类像素点相似度较高的像素点容易着色为物体的颜色,引起颜色溢出。为了改善这种情况,引入了有偏的损失函数。

有偏的损失函数是在交叉熵的基础上,对不同类别的损失进行加权。交叉熵是一种常用的分类损失函数,用来衡量两个分布之间的相似性。假设p表示真实标记的分布,q为训练后的模型的预测标记分布,那么交叉熵衡量的是真实标记的分布和预测标记的分布之间的相似性,可以表达为

(11)

考虑到与背景类相似度较高的像素点往往分散在整幅图像,且与需要上色的物体的像素点接壤,如果这类像素点被错分为其他类则会造成颜色外溢。为了使得与背景类相似度较高的像素点在预测时尽量不被预测为其他类,在训练过程中,若是背景类的像素点被错分成其他类,将给予一个较大损失,使得训练得到的模型对背景类像素点较为敏感。因此可以得到有偏的损失函数的表达式为

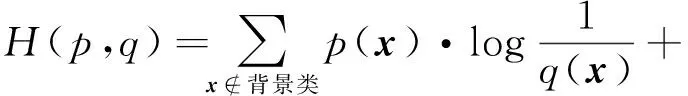
(12)

式中α表示背景类与非背景类之间的偏倚程度,在实验中设置为3.0。

3.2 模型结构

模型采用双分支的卷积神经网络,具体的模型结构如图6所示。第1个分支的输入为笔触覆盖的像素点的邻域,用于提取该邻域像素块的视觉特征;第2个分支的输入为该像素点对应的坐标位置,用于提取位置特征。而该像素点对应的颜色则作为分类的标签。

对于笔触覆盖的像素点i,首先以该像素点为中心,选取9×9的邻域作为第1个分支的输入。第1个分支使用两层的组合卷积提取特征,首先使用64个3×3的组合卷积提取特征,再做最大池化;第2层使用128个3×3的组合卷积提取特征,再做最大池化。最后对池化后的特征图进行逐像素展开并拼接,得到一个512维的一维向量,待与第2个分支的特征融合。

图6 网络模型结构Fig.6 Network model structure

同时对上述像素点i,选取其坐标位置作为第2个分支的输入,这里的坐标以图像左上角为原点。第2个分支使用含256个节点的全连接层提取位置特征,得到1个256维的一维向量。模型将第1个分支的512维向量与第2个分支的256维向量拼接,形成1个768维的一维向量,再对这个融合后的特征向量使用一个含256个节点的全连接层提取最终的特征向量。最后使用softmax函数作分类,得到分类概率向量。

预测时,使用SLIC算法[16]将整幅图像进行超像素分割,然后根据分割后的超像素块计算每一块的平均坐标,作为该超像素块的中心坐标。这里的坐标值都是以图像左上角为原点的相对坐标。由于平均坐标值一般为浮点数,这里采用向下取整的方式,得到一个二维的整数型向量,作为第2个分支的输入。最后根据得到的这个整型中心坐标,选取其9×9的邻域作为第1个分支的输入。在得到了测试集之后,使用训练好的模型进行类别预测,得到每一个超像素块的颜色标签,最终实现编辑传播。

4 实验分析

实验计算平台采用NVIDIA GeForce 940MX的图形处理器(GPU),搭载于Intel Core i7-6700 CPU,内存4 GB的笔记本。模型的代码实现是基于Keras框架,后台基于TensorFlow。实验的数据来自于DeepProp[7]和网络,实验结果如图7所示。

由于上述双分支卷积神经网络模型的第1个分支的计算量明显多于第2个分支的计算量,因此模型在训练时,采用DeepProp[8]的2阶段训练方式。首先对第1个分支进行预训练,只提取视觉特征。预训练时,输入为9×9的超像素块,使用第1个分支提取特征后,不经过特征融合而直接进行2个全连接的操作和softmax分类,得到分类概率向量。预训练时设置每批的样本数量为10,并且设置最多进行10期的训练。预训练结束后得到第1个分支和全连接层的参数,将这些参数作为第2阶段微调训练时的初始参数,然后进行训练。微调训练时,设置每批的样本数量也为10,并且当损失函数减少幅度小于0.01时,终止训练。

在实验中,由于笔触覆盖的像素点距离较近,像素点覆盖的9×9的邻域较为相似,因此训练数据存在较大的冗余。在实验中为了使图像训练和预测的时间相对较短,同时考虑和DeepProp[8]的实验设置保持一致,增强对比性,实验中随机选取了笔触覆盖的像素点的10%进行训练。实验中训练样本的数量取决于笔触的多少,训练过程中,采用了Adam算法[17]进行后向传播,初始的学习率设置为0.001。在使用SLIC算法[16]进行超像素分割时,设置将图像分割为[w×h×0.01]个超像素块,其中w表示图像的宽,h表示图像的高,[]表示向下取整。

通过对比实验,可以发现改进后的卷积神经网络模型可以较好地改善颜色溢出的情况。对于图7中第1行的实验数据,观察局部的放大图,可以发现笔者的方法使得花瓣边缘的颜色更加清晰,颜色没有溢出。而图7中第2行的实验数据,图片中的物体轮廓较为清晰,同时背景简单,笔者的方法能够很好地对图像中物体上色,并没有发生颜色溢出的情况。观察图7第3行和第4行的实验数据,笔触图均为灰度图,相对于彩色图片失去了色彩信息,然而使用笔者构建的双分支卷积神经网络模型也能较好地提取图像的特征,实现图像的编辑传播。相比于其他方法,笔者的方法对图像中的物体着色更加完整,视觉效果更加美观。

图7 实验结果Fig.7 Experimental results

5 结 论

基于改进的卷积神经网络进行图像编辑传播,使用由可变形卷积和可分离卷积组成的组合卷积提取图像特征,可以得到更合理的特征,使得模型的泛化能力更好,并且不会对模型的参数量和计算量增加负担。有偏的分类损失函数对不同类别的分类损失加以权重,使得模型对背景类像素点更加敏感,能够有效地改善颜色溢出的情况。使用笔者构建的双分支卷积神经网络模型可以很好地实现图像的编辑传播,同时该模型也支持对灰度图的上色。使用笔者提出的方法可以加快对图像的色彩处理,然而对于颜色复杂的场景该模型表现较差,在未来可以考虑更有效的模型结构。