基于热学参数反演分析的常态大坝混凝土温度场仿真

,,

(1.浙江工业大学 建筑工程学院,浙江 杭州 310023;2.浙江省水利河口研究院浙江省水利防灾减灾重点实验室,浙江 杭州 310020)

在大坝施工过程中,水泥水化放热,导致混凝土存在基础温差和内外温差,并产生较大拉应力,从而会使大坝产生大量的裂缝[1-3]。为减少混凝土施工期裂缝,提高大坝运行可靠度,施工中常采用相应的温控防裂措施以满足大坝的耐久性要求。为指导大体积混凝土施工,减少施工期温度裂缝的产生,可根据现有的混凝土温度场和应力场理论对施工期大坝温度场和应力场进行仿真[4],并与施工期监测温度和应力进行对比分析,进而提出针对性的温控防裂措施。

混凝土热学参数的选取对于其温度场仿真模拟影响较大,是混凝土温控防裂方案确定的关键之一[5-7]。目前热学参数主要通过室内试验及经验公式所得,但是这两种方式均存在一定的弊端:室内试验花费高、耗时长;经验公式误差较大,与实际工程相差较大[8-10]。因此,获得可用于后续施工的仿真计算结果,需得到准确的相关参数来反映工程的实际情况。若是能根据不同时刻、不同空间位置的温度值对混凝土热学参数进行反演分析,则有助于把握仿真计算所需的相关热学参数,以提高仿真精度。目前,参数反演分析在实际工程中已有广泛的应用,研究成果主要集中在位移参数问题上[11],但是对于热学参数的反演研究成果尚不多见。笔者通过对常态大坝混凝土(非碾压混凝土)热学参数进行反演分析,以期得到可用于仿真计算的可靠热学参数,模拟出后续大坝施工的温度场变化,以便及时采取相应的温控措施。

1 工程概况

潜明水库位于浙江省缙云县和磐安县境内,坝址位于瓯江流域好溪缙云县境内的左库水库附近,坝址以上集水面积304.8 km2,水库坝址距壶镇约6.5 km,距缙云县城约25 km,距丽水市区约63 km。其拦河坝为常态混凝土重力坝,坝顶高程247.0 m,防浪墙顶高程248.2 m,河床段建基面高程204.5 m,相应最大坝高42.5 m。坝顶按一般交通要求布置,坝顶宽5 m,坝顶长335 m。

2 现场原位试验

2.1 试验原材料与配合比

现场原位试验使用缙云红狮水泥有限公司P.O-42.5普通硅酸盐水泥,掺量为30%的兰溪天达环保建材有限公司Ⅱ级粉煤灰,掺量为2.0%的杭州奥飞建材科技有限公司HQ-3缓凝高效减水剂,细骨料为产自当地的机制砂,粗骨料为当地的5～20,20～40,40～80,80～120 mm碎石,试验配合比如表1所示。

表1 混凝土配合比Table 1 Mix proportion of concrete kg

2.2 温度测点布置

为了解坝体混凝土绝热温升、表面放热系数、导温系数、导热系数和比热等热学参数,提高温度场计算精度,本次在施工现场进行原位试验观测。在11号坝体内部布置5个温度计,温度计采用葛南实业的RT-1型电阻温度计,如图1所示。

图1 电阻温度计Fig.1 Resistance thermometer

在测点的埋设位置上,选取仓面中间的表面和内部,如图2所示,温度计探头平行于表面布置,以全面了解大坝混凝土温度的变化情况,提高反演精度,以便制定合理的大坝混凝土的温控措施。

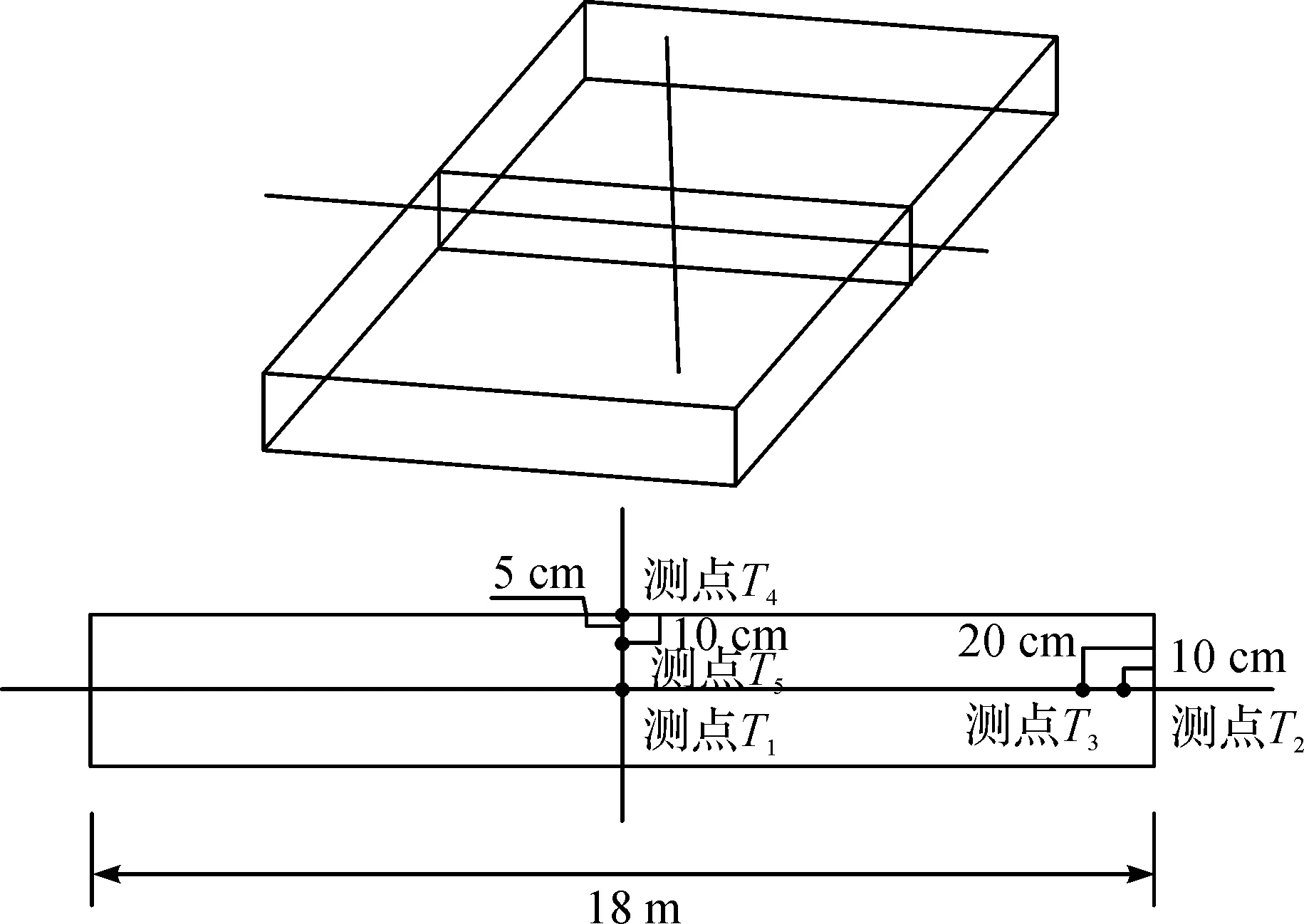
图2 原位测点埋设示意图Fig.2 Sketch map of in-situ observation point

2.3 实测温度

混凝土入仓前观测1次;入仓后至达到峰值(约3～4 d),每2 h观测1次;达到峰值后1 d内,每4 h观测1次;此后每8 h观测1次,连续观测约2周。用1～5号温度计所测原位观测点的温度详见图3,混凝土入仓温度13 ℃左右,内部点最高温度为33.0 ℃(出现在浇筑后4～5 d)。

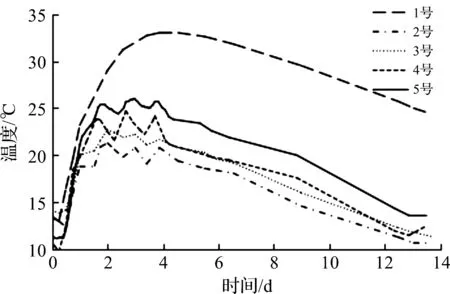
图3 原位观测点实测温度Fig.3 Measured temperature of in-situ observation point

3 热学参数反演

对大坝施工期进行温度场仿真模拟,并采取相应的温控防裂措施是目前用来指导工程施工的常用方法。在大坝施工过程中,外部环境温度和材料热学参数是影响混凝土温度的主要因素。在仿真计算中,外部环境温度常由大坝当地温度长期观测确定,而材料热学参数包括混凝土绝热温升θ,比热c,表面放热系数β,导热系数k,导温系数a等常由经验或试验所得,但与实际工程有所差异。现已知外部环境温度及原位试验数据,选取c,β,k,a等4个参数作为反演参数。

3.1 混凝土绝热温升

混凝土绝热温升为其周围无任何散热条件、无任何热损耗情况下,水泥水化产生的水化热全部转化为升温后的温度,可作为衡量反应放热程度的指标,是混凝土的一项重要性能指标。这一指标会影响混凝土的水化热温升、最高温度、基础温差及内外温差等,对于大体积混凝土而言,影响更大。目前在仿真程序中广泛使用的绝热温升表达式有指数式、双曲线式和复合指数式3种。其中,指数式便于数学运算但与试验资料吻合程度较差,后两种吻合程度较好但不利于数学运算。而当遇到缺乏可直接测定的相关资料的情况时,混凝土的绝热温升值[5]可通过水泥水化热进行估算,即

(1)

式中:W为水泥用量;c为混凝土比热;ρ为混凝土密度;F为混合材用量;Q(τ)为水泥水化热;k为折减系数,对于粉煤灰,可取k=0.25。由原位试验混凝土配合比估算得混凝土绝热温升曲线,如图4所示。

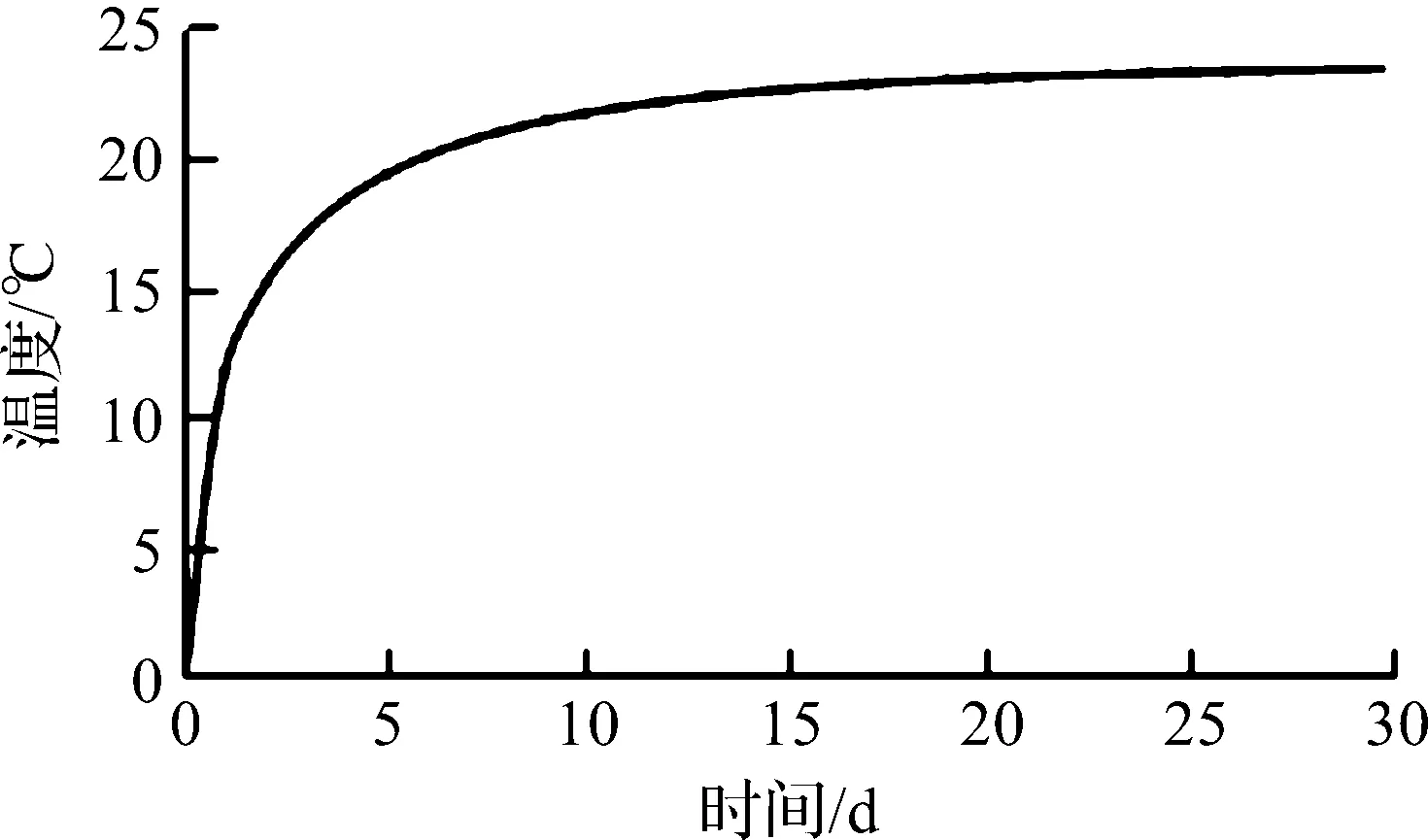
图4 混凝土绝热温升曲线Fig.4 Adiabatic temperature rise curve of concrete

3.2 环境温度

外界温度的变化对大体积混凝土的温度场及应力场的变化影响很大,混凝土拌和、浇筑及后期运行中的气温变化是混凝土开裂的重要原因,在工程实际及仿真模拟计算中须考虑气温变化的影响。夏季温度较高会产生压应力,而冬季温度较低会使混凝土内部产生较大的拉应力,当超过允许拉应力时,就会造成混凝土的开裂。此外,气温会直接影响混凝土的拌和温度和入仓温度等,进而直接影响混凝土的浇筑温度。1年中气温的变化规律主要与季节有关,可分为年变化周期、月变化周期及日变化周期。在此次仿真计算中,环境温度采用金竹站实测环境温度,将气温按月用余弦函数表示为

(2)

式中:Ta为月平均气温,℃;τ为时间,月。

3.3 参数反演分析

遗传算法借鉴适者生存、优胜劣汰遗传机制演化而来的一种计算模型,采用简单的编码技术来表示各种复杂的结构,并通过对一组编码进行简单遗传操作和优胜劣汰选择来指导学习和确定搜索方向。遗传算法的操作对象是一群数字串(称为染色体、个体),即种群,每一个染色体都对应问题的一个解。从初始种群出发,采用基于适应值比例的选择策略在当前种群中选择个体,使用杂交和变异来产生下一代种群,以此模仿生命的进化直至满足期望值的终止条件为止。这一算法为解决最优化问题提供了一个有效的途径和通用框架,开创了一种新的全局优化搜索算法。加速遗传算法则是在该算法的基础上,利用最近两代进化操作产生的优秀个体的最大变化区间重新确定基因的限制条件,重新生成初始种群,再进行遗传算法运算。如此进行循环运算,可进一步充分利用进化迭代产生的优秀个体,快速压缩初始种群基因控制区间的大小,提高遗传算法的运算效率。为提高运算效率,采用加速遗传算法进行热学参数反演分析。

建立三维有限元仿真计算模型,用基于fortran 6.5编制的"温控仿真计算程序"[12]进行温度场反演分析。反演分析初始值参照《大体积混凝土温度应力与温度控制》[5],见表2。反演计算采用8节点六面体等参单元,有限元仿真计算模型见图5,共划分节点22 638个,单元19 310个,并在原位试验中大坝所埋设温度计位置设置相对应的节点,以便仿真值与实测值进行对比分析。

表2 热学参数反演初始值

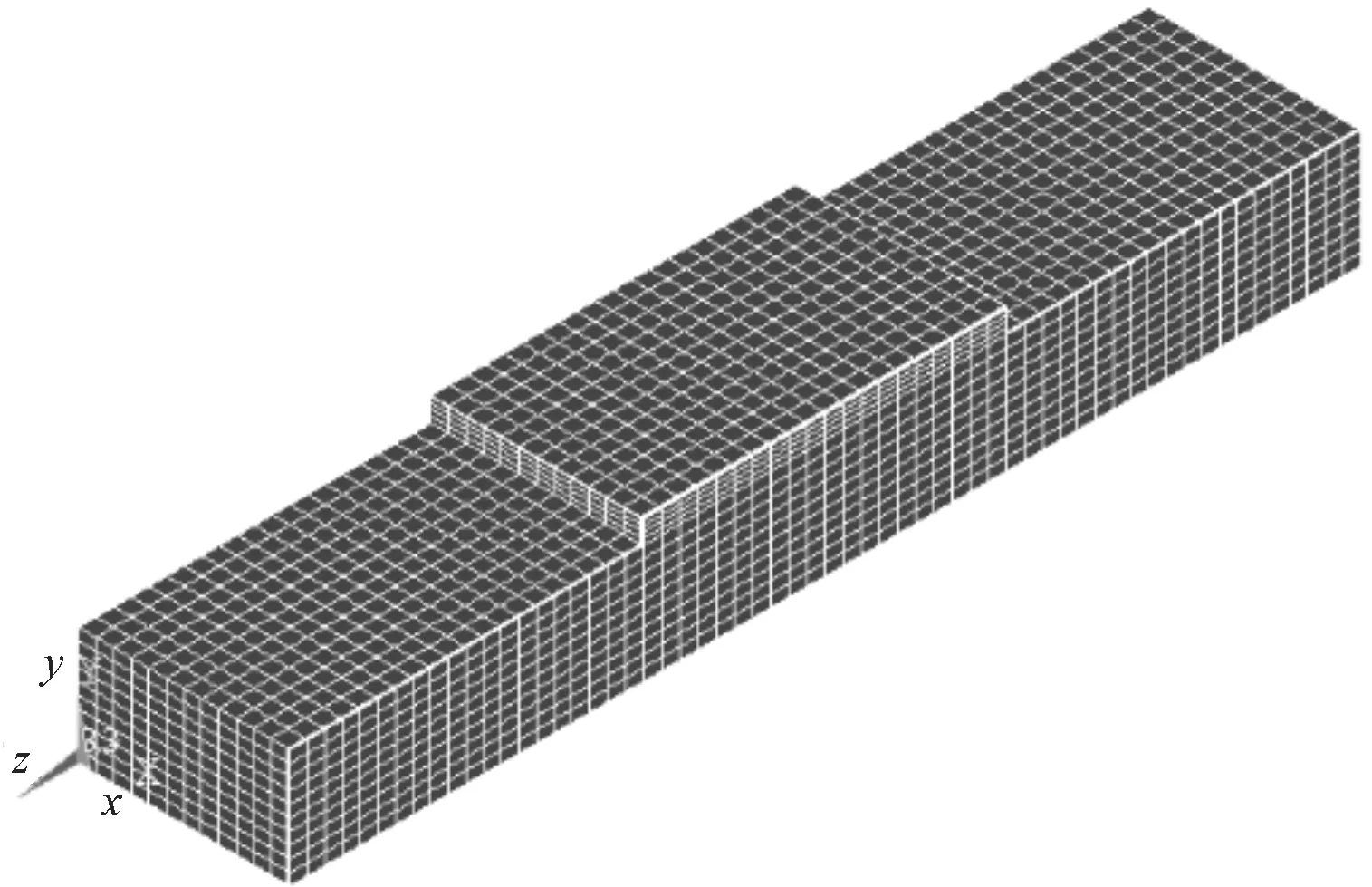
图5 有限元仿真计算模型Fig.5 Simulation calculation model of finite element

温度场计算时,地基初始温度的确定方法:取坝体地基初始温度为常数,如多年平均气温,再根据坝址处的年气温变化,对地基进行非稳定温度场的仿真计算。仿真计算中,假定计算域内岩体底面及四周均为绝热边界,坝体上下游和混凝土的浇筑层面为热交换边界。11坝段2016年12月30日开始浇注第1仓,采用1 cm厚木模板,浇筑后仓面用毛毡进行保温。根据热学参数反演仿真,混凝土热学参数指标见表3。

表3 混凝土热学参数Table 3 Thermal parameters of concrete

将反演所得混凝土热学参数运用到仿真计算程序中,经Tecplot软件处理,可得相应的坝体特征点温度历程曲线,如图6～10所示。

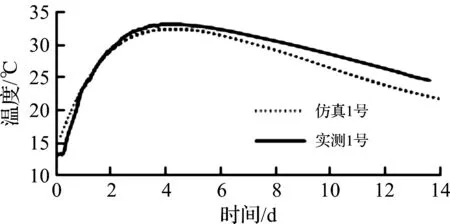
图6 中心测点实测温度和拟合温度Fig.6 Measured temperature and fitting temperature of center measuring point

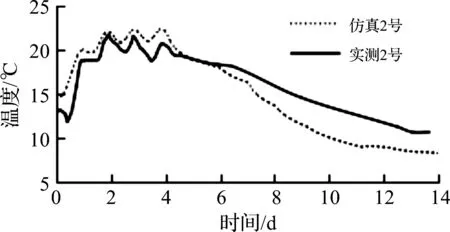
图7 距侧面10 cm测点实测温度和拟合温度Fig.7 Measured temperature and fitting temperature of 10 cm measuring point from side

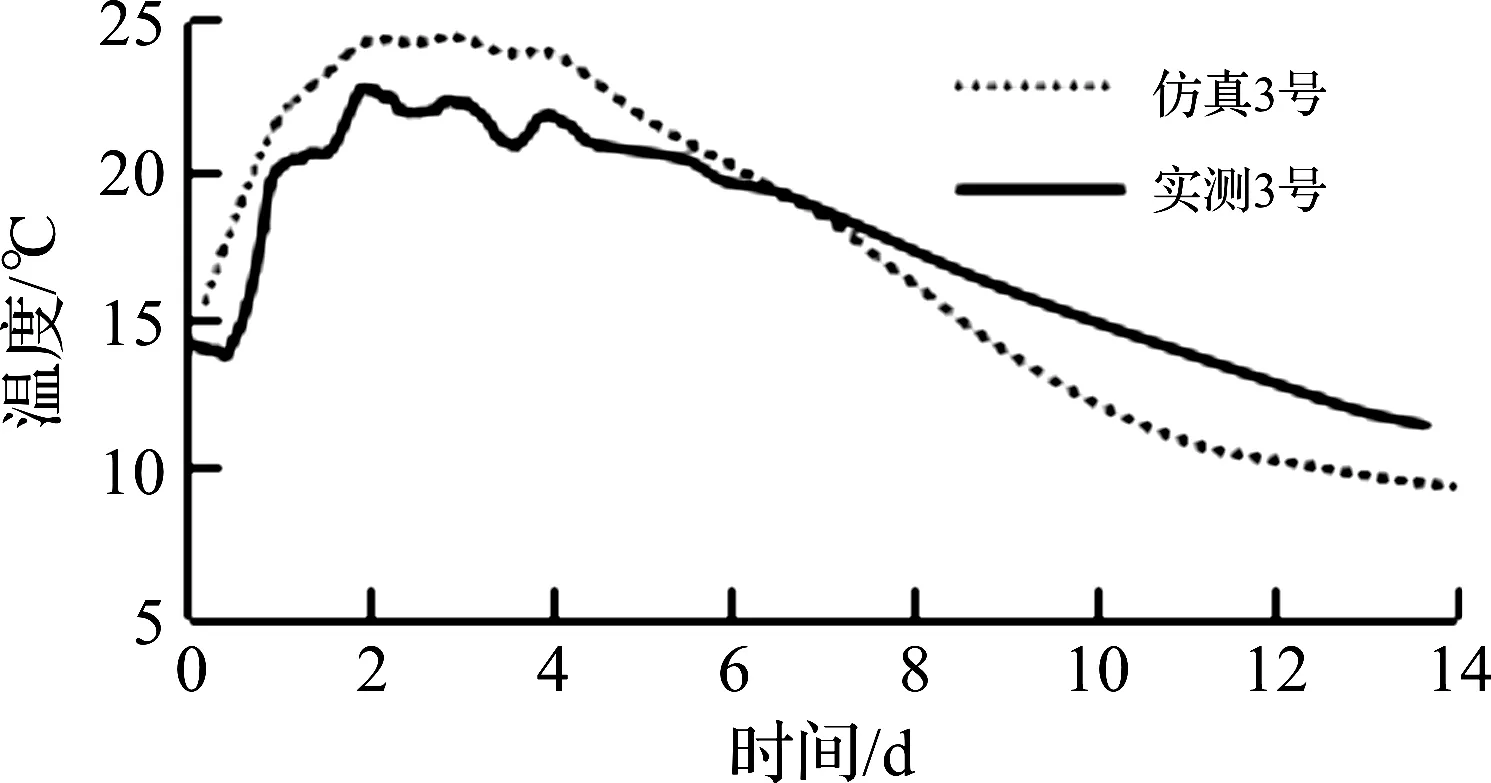
图8 距侧面20 cm测点实测温度和拟合温度Fig.8 Measured temperature and fitting temperature of 20 cm measuring point from side

图9 距仓面5 cm测点实测温度和拟合温度Fig.9 Measured temperature and fitting temperature of 5 cm measuring point from the warehouse surface

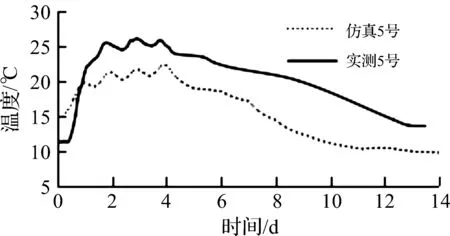
图10 距仓面10 cm测点实测温度和拟合温度Fig.10 Measured temperature and fitting temperature of 10 cm measuring point from the warehouse surface

从图6～10可知：仿真计算所得温度曲线与相对应的温度实测曲线的变化趋势和基本温度值都大致吻合。其中从实测温度和拟合温度的最高值看,在内部测点T1两者的最高温度基本相等,距侧面10 cm测点T2和距侧面20 cm测点T3的最高温度仿真值略大于实测值,而距仓面5 cm测点T4和距仓面10 cm测点T5的最高温度仿真值则比实测值低大概5 ℃。仓面与侧面温度仿真值与实测值的不同偏差与仿真程序中所设不同放热系数有关。程序通过调整放热系数来简化实际工程中所采取通冷却水管的措施,而对仓面、侧面及地基采用不同放热系数则是用来提高仿真精度。

相对而言,测点T1,T2,T3的仿真计算值与实际值拟合程度较好,而T4,T5两个测点拟合情况相对较差。除了上述放热系数不同外,主要是因为混凝土表面的温度梯度较大,且施工过程中探头埋设可能有所移动。此外,越接近混凝土表面的测点受外界温度变化影响较大,而在仿真计算中,所用环境温度为当地实测温度经余弦函数拟合所得。因此,由于仿真所用温度与实际环境温度存在一定的差异也使得接近混凝土表面的测点仿真值与实测值有一定的差距,但是两者的差距较小。由此可见:根据现场原位试验,反演得出的混凝土热学参数基本能反应混凝土热学特性,从而能提高大坝混凝土内部温度预报与温度场仿真计算结果的可信度,可作为施工期仿真计算的热学参数。

4 结 论

通过现场原位试验,测得各测点不同时刻的温度值。由反演分析所得的混凝土热学参数用于温度仿真计算,所得计算值与其实测温度值比较分析,可得两者吻合较好。由此可见:反演所得热学参数值可用于大坝混凝土温度场仿真计算。现场原位测试法结合反演分析方法所得热学参数较室内试验、经验公式等所得参数更为准确简便,是确定大坝温度场仿真计算所需热学参数的有效方法。

本文得到深圳大学广东省滨海土木工程耐久性重点实验室开放基金项目(GDDCE15-01)和浙江工业大学研究生教改研究课题(2016-ZX-236)的资助。