浅谈独立性检验的思想在统计分析中的应用

张清良

[摘           要]  浅析通过独立性检验思想方法的应用来分析多个分类变量之间的关系，进一步感受独立性检验的思想在现实生活中的应用。

[关    键   词]  独立性检验;多个分类变量;应用

[中图分类号]  G642            [文献标志码]  A          [文章编号]  2096-0603（2019）31-0190-02

独立性检验思想方法在医学分析、教学评价、现实生活等各个领域都有重要的作用。那么，如何将抽象的数学理论应用到具体的生活实践中去？本文通过独立性检验的思想方法探讨现实生活问题分类变量的相互关系。

一、独立性检验的基本思想

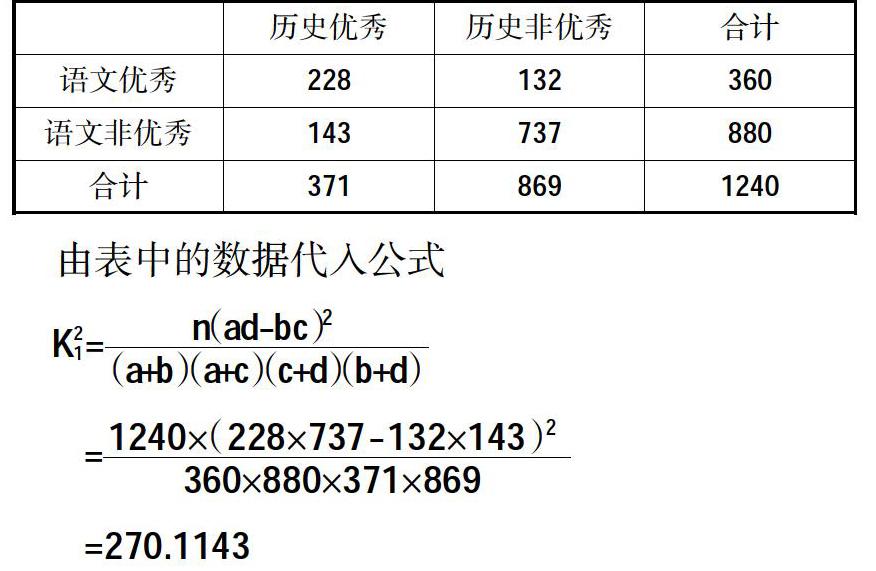
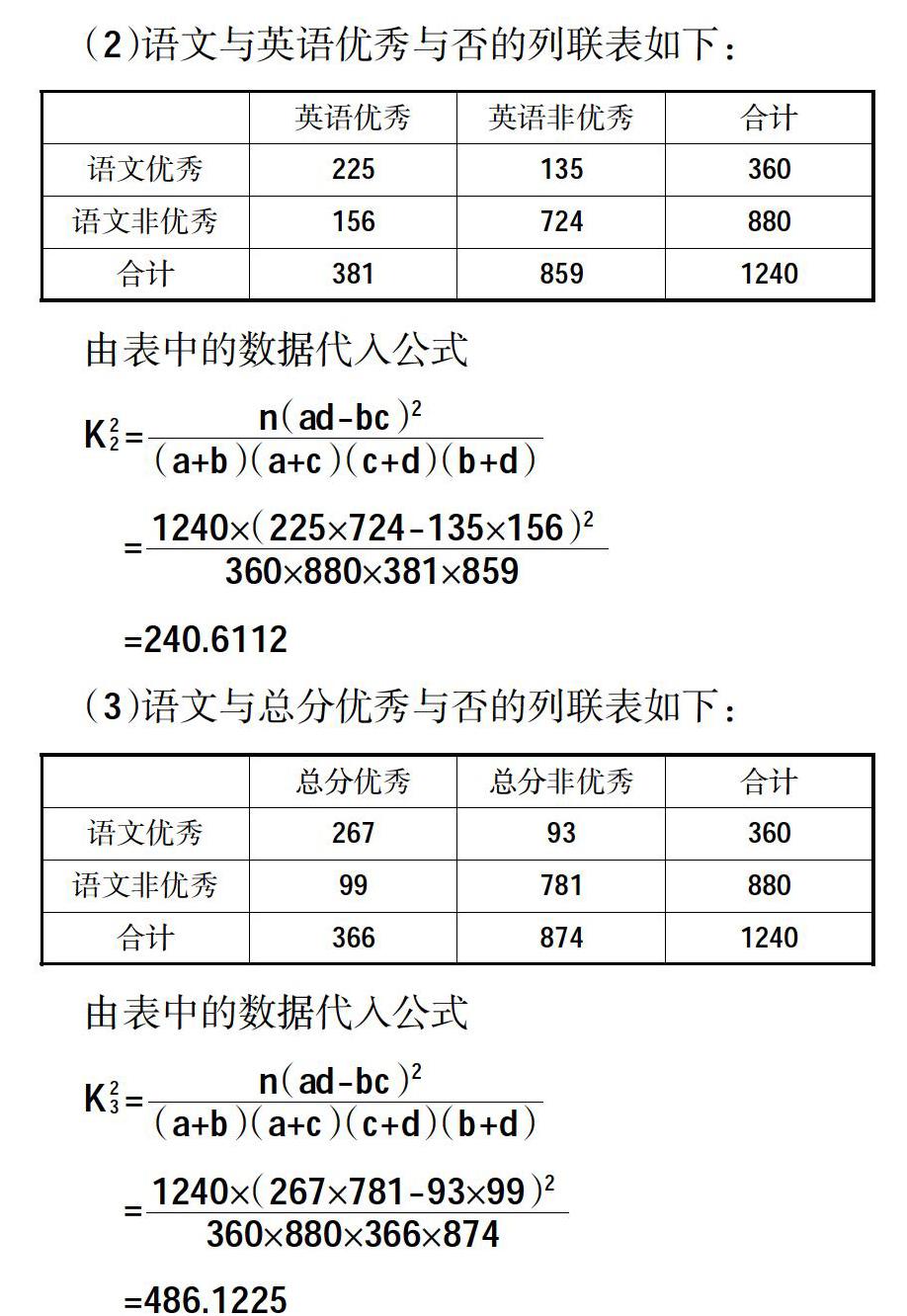
在日常生活中，分类变量是大量存在的，例如吃槟榔与患口腔癌等，在实际问题中我们常常关心两个变量之间是否有关系，从直观上看吃槟榔与不吃槟榔患口腔癌的可能性是存在差异的。假设事件Q与E和F没有关系，若Q成立，即E与F没有关系，则K2应该很小，只需要计算出K2或K2的观测值k=■的大小，其中n=a+b+c+d为样本容量。在Q成立的条件下，统计学家估计出的概率P（K2≥6.635）≈0.01即在Q成立的情况下K2的值大于6.635的概率非常小，近似于0.01，也就是说，在Q成立的情况下，对随机变量K2进行多次观测，观测值超过6.635的频率约为0.01，如果K2≥6.635，就可以判定Q不成立。因而E和F有关系成立，并且我们有99%以上的把握认为E与F的有关系成立。

利用隨机变量K2来确定在大多程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验。独立性检验的基本思想类似于反证法。要确认“两个分类变量有关系”这一结论成立的可信度，需要假设“两个分类变量没有关系”成立，在该假设下构造的随机变量K2应该很小，如果由观测数据计算得到的K2的观测值很大，则在一定程度上说明假设不合理，根据随机变量K2的含义，可以通过概率P（K2≥6.635）≈0.01来评价该假设不合理的程度，由实际计算出的k≥6.635，说明该假设不合理程度约为99%，即“两个分类变量有关系”这一结论成立的可信程度约为99%。

二、独立性检验的实际应用

利用独立性检验解决实际问题的步骤为：

（1）K2=计算。

（2）比较K2与四个临界值：2.706，3.841，5.024和6.635的大小。

（3）利用K2检验值为依据也可能有失误，它强调的是最大的可能性。其样本越大，这个估计值越准确。使用K2统计量作2×2列联表的独立性检验时，要求表中的四个数大于5，因此，在选取样本容量时一定要注意这一点。

三、实例分析

实例1：对某校做一次大型调查，语文成绩优秀和非优秀的学生中，历史、英语、总分也为优秀的人数如下表所示，则语文成绩优秀与历史、英语、总分也为优秀哪个关系较大？

所以有99%的把握认为其亲属的饮食习惯与年龄有关。

四、在日常生活中，分类变量是大量存在的

例如，户外运动是否与性别有关;大学生每周运动时间是否与性别有关;中年人秃发是否与心脏病有关;了解某种疾病是否与性别有关等。都可以随机对自己要调查研究的问题抽取样本进行问卷调查，利用独立性检测来考查两个分类变量是否有关联关系，并且能比较精确地给出这种判断的可靠程度。具体做法是：根据观测数据计算由（1）式给出的检验随机变量K2的值k，其值越大，说明“X与Y有关系”成立的可能性越大。当得到的观测数据a，b，c，d都不小于5时，可以通过查阅下表来确定结论“X与Y有关系”的可信程度。

五、结语

在准确理解实际问题的基础上正确建立数学模型，然后应用独立性检验思想方法来分析多个分类变量之间的关系，对实际问题作出正确的判断有着十分重要的作用。

参考文献：

[1]郭金，韦程东.在数值分析教学中融入数学建模思想的研究与实践[J].广西师范学院学报（自然科学版），2008，25（3）：124

[2]闵杰，李义宝.高校数值分析课程组合式教学方法探索研究[J].高教论坛，2001（6）：72.

[3]袁荫棠.概率论与数理统计[M].北京：中国人民大学出版社，1989.

编辑 张 慧