新股申购效率的定义、计算和性质 及家庭内股票资产均分定理

摘   要：本文首次定义了“新股申购效率”（简称“打新效率”），由此可求出任意持股市值下的打新收益;原创性地定义了“个股的打新效率”、“市场的打新效率”，推导计算公式及相关性质，作出函数图像;定义了“打新收益金额函数”，证明其凹性。在此基础上，本文提出并证明了“家庭内股票资产均分定理”，得出股票市值在所有家庭成员的账户中均分时可获得最高的打新收益，应以家庭（而非个人）为最小单位来研究股票配置，新增股市开户数不能再作为判断股市热度及人气的指标。随财富的增加，增持股票的意愿会逐渐下降。

关键词：新股申购;打新收益金额函数;个股的打新效率;市场的打新效率;家庭内股票资产均分定理;资产配置

DOI：10.3969/j.issn.1003-9031.2019.12.001

中图分类号：F830.91           文献标识码：A             文章编号：1003-9031（2019）12-0003-11

2016年1月，《完善新股发行制度相关规则》（以下简称新制度）中规定，证监会对新股进行常态化发行，但对新股市盈率进行控制，申购新股无需预先缴款，只要有足够股票做底仓，每周均可“0成本”地申购所有新股。投资者通常会顶格申购，如有中签，会缴款参与认购，待连续涨停板打开后卖出。

Coenelli&Goldreich（2001，2003）认为新股抑价现象在国际上普遍存在，新股大比例超额申购导致二级市场价格扭曲。Dorn等（2009） 研究了德国新股申购情况及上市首日涨幅，认为参与新股申购及新股上市首日交易的投资者会随着股市上涨，情绪火爆而显著增多。Boulton等（2011）研究了34个主要国家和地区的7306个IPO项目，发现欧美日韩等主要资本市场的IPO平均抑价率中枢区间为15～58%。

IPO抑价现象在我国也一直存在，理性和非理性因素共同推动新股上市后股价大幅增长。刘超（2017）计算出2016年持有1万元市值时的“打新收益率”沪市为17.83%，深市为19.36%。IPO抑价带来的巨大的、近乎无风险的财富，会对我国数以亿计的投资者的资产配置方式造成重大影响。

一、新股发行情况

（一）新制度下网上申购市场具有公平性、信息高度公开性、低门槛性

公平性：每个人的中签概率仅与持有市值高低及该新股超额认购倍数有关。沪市为每1万元市值获得一个配号，每配号1000股。深市为每0.5万元市值获得一个配号，每配号500股。获得的配号数不超过该股的申购上限。摇号决定某配号可否获得新股申购权。一人仅可用一个账户打新。

信息高度公开性：几乎所有券商的股票交易软件都在显著位置展示新股发行信息，且提供“一键打新”，只需点击一个按钮就可申购当日新股。

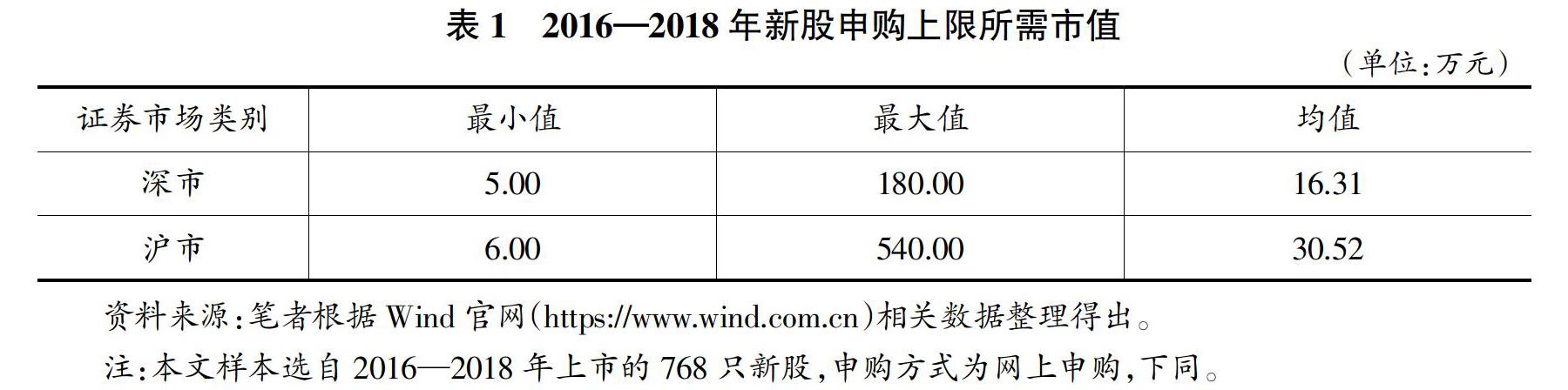
低门槛性：只需持有1万元沪市或深市市值，即可参与该市场所有新股申购（见表1）。

（二）新制度下的新股抑价红利依然巨大

刘超（2017）原创性地定义了网上申购新股的收益率（即打新收益率）=。参考该论文方法，可计算持有1万元沪市、深市市值在2016—2018年的“打新收益率”（见表2）。

二、打新效率的定义和性质及实证研究

（一）“打新效率”的定义

由表2可知，2016年每日都持有1万元沪市市值，打新收益率为17.83%。若持有2万元沪市市值，可以申购所有沪市新股2签。相比1万元市值时，申购新股获得收益增加至2倍，打新收益率仍为17.83%。若每日都持有的沪市市值增加至100万元，会出现持股市值超过某些新股申购上限的情况。相比1万元沪市市值而言，100万元市值所获得的打新收益会增加，但打新收益率应在0～17.83%这一区间。因此，我们需要定义一个变量，它能以百分比的形式反映所持市值可以用于新股申購的比例，同时方便我们计算出任意市值对应的“打新收益率”。这一变量即“新股申购效率”，简称“打新效率”。

（二）个股的“打新效率”的定义、计算及性质

对某只新股而言，可以定义打新效率α（x）：投资者持有该市场市值x万元时，申购该新股获得的收益与假定所有市值都能申购新股的收益之比。特别指出，“打新效率”必须沪市深市分开考虑。如沪市的α（x）中的x为持有的沪市市值x万元，α（x）所涉及的新股样本也必须是沪市的。打新效率遵循下面的假设：对每个新股都进行最大限度的网上申购，且中签后缴款认购;新股上市首日收益为非负值，开板即卖出;投资者每日持有沪市或深市市值为定值x;不考虑卖出新股后所得收益的再投资。

若申购人所有市值都能申购新股，则“持有该市场市值x万元时的打新收益”等于“持有1万元市值的打新收益的x倍”。因此，

即α（x）是可被用于申购新股的市值与总市值x的比值。若沪市新股申购上限所需沪市市值为N万元，则：

α（x）=，X>0  （2）

其中，[x]为取整，下同。

如深市新股申购上限所需深市市值为0.5*N万元，则：α（x），X>0。可以推导出沪市个股的打新效率α（x）的一些性质：0≤α（x）≤100% ;当且仅当X为正整数X≤N时，有α（x）=100%。

（三）打新收益金额函数

定义“打新收益金额函数”A（x）为一段时间内，日均持有x万元市值时，在该市场参与所有新股申购而获得总收益的期望值。A（x）、x的单位均为万元。A（x）需指明对应的市场为沪市或深市。

A（1）是一个常数，仅与时间、市场有关。A（1）的意义有两个：一是日均市值1万元时的打新收益的期望值;二是若把A（1）看成是，则A（1）为日均市值1万元时的通过在该市场申购所有新股而获得的“打新收益率”。在新股至少上市首日收益非负的假设下，A（x）≥0。由表2可知：对沪市，A2016（1）= 17.83%，A2017（1）= 16.72%，A2018（1）=6.41%;对深市，A2016（1）= 19.36%，A2017（1）= 17.03%，A2018（1）= 5.13%。

假定一段时间内，沪市有k个新股发行，对i=1…k，第i个新股每个配号中签率为Pi、申购上限配号数Ni，每一配号（1000股）开板收益Si，则：

（4）

下面证明打新收益金额函数的凹性性质：

该凹性性质可以表述为：打新收益金额函数在正整数域上有凹性或忽略零头市值的影响时，打新收益金额函数有凹性。这一性质在下文证明“家庭内股票资产均分定理”时会起到重要作用。由于对市值更细致的划分，深市的打新收益金额函数在0.5倍数的数域上有凹性，证明类似。

（四）市场的“打新效率”的定义、计算、性质

本文可定义市场的打新效率θ（x）：某一段时间内，投资者日均持有该市场市值x万元时，“申购该市场所有新股获得的打新总收益”与“假定所有市值都能用于申购所有新股的打新总收益”之比。

假定所有市值x（万元）都能用于申购所有新股，此时打新总收益为x*A（1），则打新效率θ（x）的表达式为：

变形得到：

我们可得沪市市场打新效率的公式：

类似可得深市打新效率：

易证沪市θ（x）的一些性质：

性质1.0≤θ（x）≤100%;

性质2.当且仅当X为正整数X≤min（N1，N2…Nk）时，有θ（x）=100%。

类似地，深市“打新效率”达到100%，当且仅当市值未超过该市场所有新股的申购上限且市值为0.5的整数倍。

性质3.θ（x）≤θ（[x]），沪市零头部分市值无法参与打新，导致打新效率下降;

性质7.若x为正整数，必有θ（x）≥θ（x+1），θ（x）在正整数域上单调递减。

深市有类似但更精细的结论：若x为0.5的整数倍且x≥1，必有θ（x）≥θ（x+0.5）

（五）“市场的打新效率”的作用

式（6）连接了打新收益率和“市场的打新效率”，体现了“市场的打新效率”的重要地位。对于任意持股市值x（万元），只要将常数A（1）乘以对应的打新效率θ（x），即可求得该市值下的打新收益率。

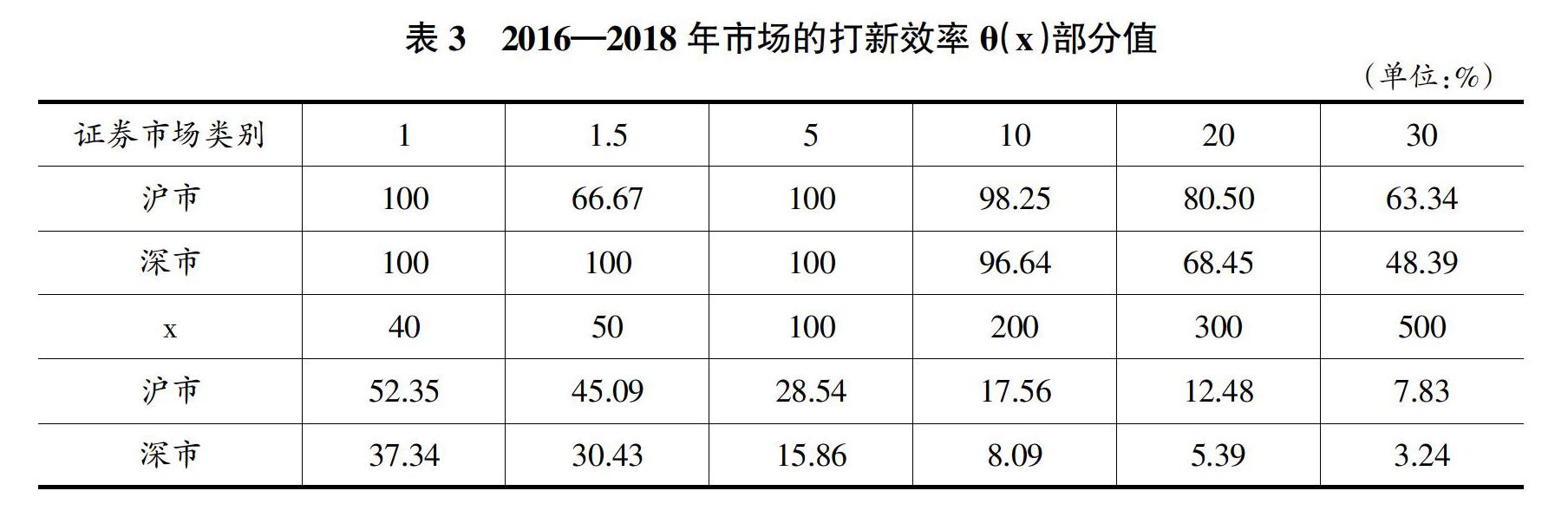
如2016年某投资者持有30万元沪市股票。若沪市“市场的打新效率”θ（30）= 63.34%，由A（1）=17.83%，可求全年打新收益率=θ（30）*A（1） =11.29%。表明：该投资者日均持有30万元沪市股票，2016年申购该市场所有新股可获11.29%收益率，收益金额30*11.29%=3.39（万元）。

（六）“市場的打新效率”的实证分析及函数图

2016—2018年上市的新股，由于每个新股中签率Pi、申购上限配号数Ni、每一配号开板收益Si为历史数据均已知，我们可以由式（7）作出沪市市场的打新效率θ（x）的函数图（见图1、2）。

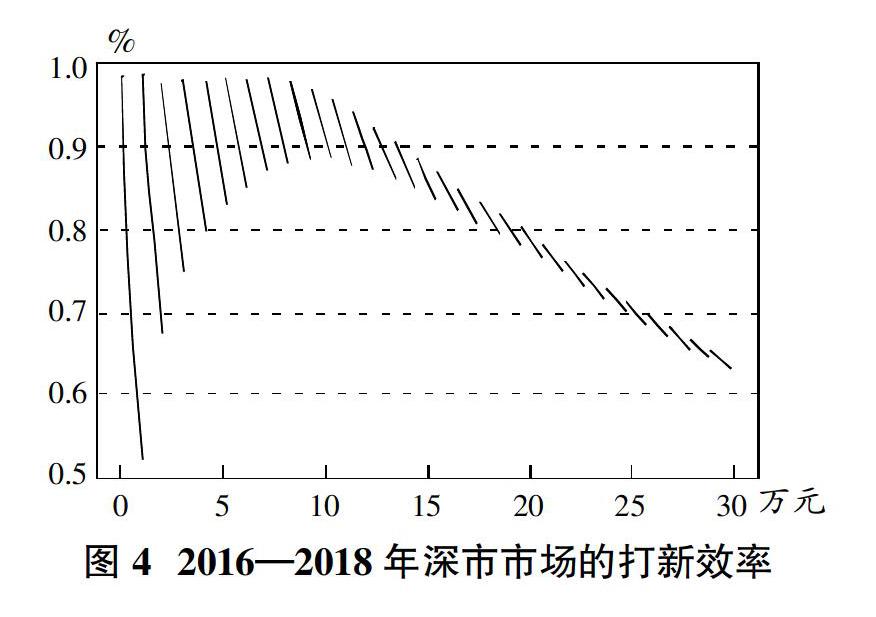
由图1可见，当持仓沪市市值超过50万元，打新效率已经近似于双曲线，满足θ（x）性质4。由图2可见，每个整数点的跳跃幅度反映了“零头市值”对打新效率的影响。随x增加，跳跃幅度减少。表明：随持仓市值增加，“零头市值”对打新效率的影响下降。当x =1，2，……6时，沪市的θ（x）=100%;满足θ（x）的性质2。同期深市θ（x）图像见图3、4，对比图2、4，可见：深市θ（x）间断点的跳跃幅度小于沪市，这是因为深市对市值与申购股数的划分更细致。

由表3可知：随x增加，深市θ（x）下降幅度明显快于沪市。这是因为深市新股多为小盘股，申购上限所需的市值较低，市值增加会更明显地导致市值浪费。

（七）市场的打新效率与个股的打新效率的关系

以沪市为例，沪市第i个新股的个股打新效率：

式（14）显示，市场的打新效率是个股的打新效率的加权平均，其中，权重wi与Si*Pi成正比。

三、家庭内股票资产均分定理

（一）“家庭内股票资产均分定理”的提出及证明

投资者的投资收益与打新效率θ（x）呈正相关。为了获得更大投资收益率，会追求更大的θ（x）。根据θ（x）的性质7知：忽略零头市值的影响，若持有的股票市值恒定，相比股票市值放在同一账户，将持有的股票市值在不同人的账户间均分可以获得更大的打新效率，从而获得更大的打新收益。

下面提出并证明“家庭内股票资产均分定理”：一个家庭持有的股票总市值恒定，则下面三种资产分配方式给该家庭带来的总的打新收益关系为：所有股票市值放在同一账户≤股票市值分散在所有家庭成员的账户≤股票市值在所有家庭成员的账户中均分。（假定各账户股票市值和均分市值为整数）证明：

下面证明上述定理：

综上，“家庭内股票资产均分定理”得证。

（二）“家庭内股票资产均分定理”的实证分析

记一个家庭内投资的股票总资产为V（万元），假设家庭仅2名成员1号、2号，且均可开设股票账户。记各账户股票资产分别为V1、V2，则V1+V2=V。

由家庭内股票资产均分定理可知，在V为正偶数时，股票资产在1号、2号账户均分，即V1=V2=V/2时家庭的打新总收益最高;股票资产全部在某一个账户时家庭的打新总收益最低。

下面研究2个账户股票金额V1、V2为任意非负整数时的情况。

1号账户V1时，家庭两个股票账户的打新总收益f（V1）为：

f（V1）=∑Ai=A（V1）+A（V2）=A（V1）+A（V-V1）   （15）

∴f（V1）=f（V-V1）

可知：打新总收益曲线关于均分点V/2对称。

由式（6）可将式（15）进一步分解为：

f（V1）=θ（V1）A（1）V1+θ（V-V1）A（1）*（V-V1）     （16）

由式（16）可求得家庭两个股票账户的打新总收益。我们研究沪深两市2016—2018年情况。

当V=50时，随1号账户股票市值V1在0-50之间的整数点上变动，家庭打新总收益（见图5）①。无论沪市还是深市：股票账户资产越接近于均分，家庭获得的打新总收益越高。

2016—2018年间，若2人家庭持有总计50万元沪市市值，则V1=V2=25时，家庭打新总收益达到最大值14.52万元，对应的打新收益率29.04%;V1=0，V2=50;或V1=50，V2=0時，打新总收益达到最小值9.23万元，打新收益率18.46%。

若同期2人家庭持有总计50万元深市市值，则V1=V2=25时，家庭打新总收益达到最大值11.76万元，打新收益率23.52%;V1=0，V2=50;或V1=50，V2=0时，打新总收益达到最小值6.32万元，打新收益率12.64%。

类似地，可分别得出V=20时，V=100时的家庭打新总收益（见图6、7）。

对比图5、6、7知：随V增大，散点图的最大值和最小值之差越大。可得：随着总资产增加，资产均分带来的超额收益越大。

（三）家庭内股票资产均分定理的应用

由家庭内股票资产均分定理可知，2016年新制度实施后，未开过股票账户的成年人的开户意愿增强，以便家庭中主动交易的投资者将本可以在一个账户中建立的股票头寸分散在不同家庭成员的股票账户，以获取更高的打新效率及收益。除了牛市开户数增加、熊市开户数减少的趋势外，我们还可以发现新股申购新制度实施后的开户数明显增加：2016年1月后，在A股开户数已经逐渐趋于饱和的情况下，即使进入熊市，仍然有每月不低于150万户的沪市新增开户数，明显高于2004—2005、2008、2012—2013年等熊市年份。

四、打新效率及“家庭内股票资产均分定理”带来的相关启示及建议

（一）新增股市开户数不能再作为判断股市热度及人气的指标

由“家庭内股票资产均分定理”可知，股票市值在所有家庭成员的账户中均分可以获得最高的打新收益，而“为所有家庭成员均开立股票账户”的前提条件下，2016年新制度实施后，月度新增股市开户数不能再作为判断股市热度及人气的指标。

（二）随财富的增加，增持股票的意愿会逐渐下降

对于均值方差模型（H.M.Markowitz，1952）、Black-Litterman模型（F.Black， R.Litterman， 1992）等绝大多数投资组合模型，均可得到下列结论：当投资者的风险偏好不随资产金额变动时，若投资者获得一笔可用于投资的增量财富，则其分配到各大类资产的金额也均等比例增加，而各大类资产的权重不变。

我国A股市场上，理性投资者会通过追求打新效率的最大化来追求打新收益的最大化。本文已证，持股市值越高，打新效率有下降趋势。因此，投资者将持股金额增加至原来的2倍，所获得的打新收益很可能小于原来的2倍。投资者获得一笔增量的财富，增持股票的意愿逐渐下降，股票的持仓权重会下降，投资者会更倾向于将每年获得的工资、奖金、遗产继承等增量财富用于除股票之外的其他投资及消费。

（三）家庭内各股票账户的操作应以家庭为最小单位来研究股票配置

绝大多数投资组合模型均是以个人为单位进行研究的，而根据“家庭内股票资产均分定理”，理性投资者会追求家庭打新总收益最大化，将本可以在一个账户中建立的股票头寸分散在各个家庭成员账户，而通常只有1人主动进行投资操作。因此，会出现同一家庭内，一个人依次连续登录各成员的股票账户进行同方向的股票买卖及新股申购的情况，各账户持股均反映了那个主动进行投资操作的家庭成员的观点，甚至会出现“家庭内账户的趋同性”，即全部成员的股票账户持股情况及买卖申购操作极为接近。因此，应以家庭（而非个人）作为最小单位来研究中国A股市场的投资行为，这对于分析判断内幕交易等行为都是有益的。

五、结语

本文填补了打新效率及其对投资行为影响等领域的空白：原创性地定义了“个股的打新效率”、“市场的打新效率”，推导计算公式及相关性质。得出“市场的打新效率”是“个股的打新效率”的加权平均;通过计算打新效率，首次计算出任意股票市值时打新收益;原创性定义了打新收益金额函数A（x），证明其存在凹性;提出只要将常数A（1）乘以所持股市值对应的打新效率，即可求得该市值下的打新收益率;得出了沪深两市的“市场的打新效率”θ（x）的函数图像，并进一步分析θ（x）变动规律。提出、证明并分析了“家庭内股票资产均分定理”：一个家庭持有的总股票市值恒定，则“股票市值在所有家庭成员账户中均分”可获得最大的打新收益;实证画出“家庭打新总收益”的散点图，得出该曲线存在对称性、市值均分时打新总收益最大、股票账户资产越接近于均分，获得的打新总收益越高。

本文最后得出相关启示及建议：新增股市开户数不能再作为判断股市热度及人气的指标;随财富的增加，A股投资者增持股票的意愿逐渐下降;家庭内各股票账户存在操作趋同性，所以应以家庭（而非个人）为最小单位来研究我国股票配置。

（责任编辑：夏凡）

参考文献：

[1]Francesca Cornelli，David Goldreich.Bookbuilding and Strategic Allocation[J].Journal of Finance，2001（56）.

[2]Francesca Cornelli，David Goldreich.Bookbuilding：How Informative is the Order Book？[J].Journal of Finance，2003（58）.

[3]Dorn，Daniel.Does Sentiment Drive the Retail Demand for IPOs？[J].Journal of Financial and Quantitative Analysis，2009，44（1）：85-108.

[4]Boulton T J，Smart S B，Zutter C J.Earnings Quality and International IPO Underpricing [J].The Accounting Review，2011，86（2）：83-505.

[5]刘超.新制度下新股收益率的理论研究及其影响因素的多元回归分析[J].浙江金融，2017 （12）.

[6]刘超.新制度下新股申购收益率的研究及其非理性因素的分析[J].金融理论与实践，2017（6）.

[7]廖伶欣.我国新股发行制度对IPO抑价的影响及对策[J].冶金经济与管理，2016（3）：34-37.