分数除法算理表征方式的选择：教师的视角

王敏 吴敏霞 赵雨晴 巩子坤

【摘   要】采用问卷调查，了解44名教师选择的“易于学生理解分数除法算理的表征方式”。调查结果显示：教师认为对学生而言，直观表征最容易理解，抽象表征比较容易理解，形式表征最不容易理解。随着任务难度增加，教师选择的分数除法算理表征方式会发生变化，即在同一模型（平均分，包含除，下同）中，直观表征的平均分呈下降趋势，形式表征的平均分呈上升趋势，抽象表征的平均分变化不大。教师认为我们所提供的由7个任务构成的学习路径是合理的，符合由易到难的规律。

【关键词】教师;分数除法算理;表征方式;学习路径

一、引言

运算能力是一项重要的素养。王光明等指出：运算正确、合理是运算能力的主要特征，理解算理是学生正确地、迅速地运算的基础[1]。因此，运算能力，不仅包括能正确地运算，更包括理解算理[2]。

分数知识是小学数学中很重要的内容，“分数除法”又是分数学习的重中之重[3]。对于分数除法而言，掌握法则很容易，而理解算理比较困难[4]。H·Wu指出，教师在进行分数除法教学时往往要求学生记住“颠倒相乘”的运算法则，这种忽视数学基本原则的教学使得数学学习变成死记硬背的学习，失去它原有的意义[5]。这导致有些学生在进行分数除法运算时，出现把被除数的分子分母颠倒再与除数相乘的错误，这是学生没有理解分数除法算理导致的[6]。

因而，如何使学生在理解算理的基础上，掌握法则，进而实现“算理贯通、理法融合”，是一项重要的研究课题。这就需要我们提供适合的表征分数除法算理的方式，设计合理的学习任务序列（即学习路径）[7][8]，以帮助学生理解算理，提升运算能力。巩子坤团队通过行动研究法，得到了有利于学生理解算理的学习路径，包括：分数除以整数[9];一个数除以分数 [10] 。

另外，研究显示：表征是判断学生对某个数学概念是否理解的重要证据[11]。理解分数除法算理，也就是能用多种表征方式来解释和说明运算法则的合理性。巩子坤等的研究表明，有四种表征方式（程序表征、直观表征、抽象表征、形式表征）[12][13][14]。本研究主要选择后三种。

我们常常说“以学定教”，就是说，要从学生的知识基础与认知特点出发，设计合理的任务序列即学习路径，采用合适的表征方式。对于分数除法的教学亦然。因此，借鉴巩子坤团队设计的问卷，从教师的视角，探查在教师的心目中：（1）学生易于理解的表征分数除法算理的方式是什么？随着任务难度的变化，这些表征方式变化的趋势是什么？（2）合理的学习路径是什么？

二、研究设计

（一）研究对象

选择来自四所不同学校的44名教师，其中男教师17名，女教师27名;23名教师教过分数除法，21名教师没有教过分数除法。教龄在0-5年的教师10名，在6-10年的8名，在11-15年的4名，在16-20年的12名，20年以上的10名。

（二）问卷编制

问卷由两部分构成，第一部分是选择题，一共7个任务。任务1到任务3为分数除以整数，采用平均分模型，即分数除以整数（被除数的分子能够被整除），单位分数除以整数，分数除以整数（被除数的分子不能被整除）;任务4到任务7为一个数除以分数，采用包含除模型（任务4到任务6为整数除以分数，分别为1除以单位分数、1除以非单位分数、整数除以分数;任务7为分数除以分数）。每个任务有三个选项，分别是直观表征、抽象表征和形式表征，请教师选择最容易理解、比较容易理解和最不容易理解的表征方式，并要求说明选择时的理由。

任务1至任务7分别为：[23]÷2，[12]÷3，[23÷5]，1÷[13]，1÷[23]，3÷[23]，[45]÷[23]（省略了情境）。

以任務5为例，玻璃杯的容量是[23l]。现有[1l]牛奶，可以倒入多少玻璃杯？

（1）直观表征。

图1   直观表征示意图

由图1可以看出： [1÷23=32（杯）]。

（2）抽象表征。

玻璃杯的容量是[23][l]，1[l]牛奶里有多少[23l]呢？

1[l]牛奶里有1个[23l];还剩[13l]。

[23l]可以装1杯;剩下的[13l]，是[23l]的一半即[12]，所以可以装[12杯]。

所以，1[l]牛奶可以装[1+12=32（杯）]。

所以，[1÷23=32（杯）]。

（3）形式表征。

[1÷23=（1×32）÷（23×32）=（1×32）÷1=1×32=32（杯）]。

问卷第二部分请教师选择问卷中呈现的分数除法的学习路径是否合理，若不合理，请提供新的任务序列。

（三）研究方法

问卷法和访谈法相结合。在教师完成问卷之后，通过访谈进一步了解教师选择各种表征方式的理由以及对问卷提供的学习路径的看法。

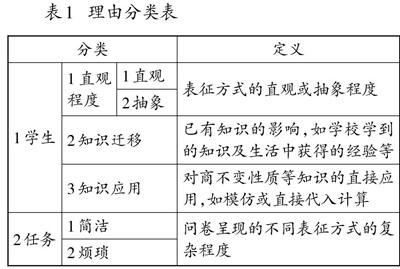
对教师的选择进行赋分，最容易理解的表征方式赋为3分，比较容易理解的赋为2分，最不容易理解的赋为1分。对教师的选择理由进行分类编码，如表1所示，2-2表示教师认为提供的表征方式比较复杂，学生不容易理解。

表1   理由分类表

[分类 定义 1学生 1直观程度 1直观 表征方式的直观或抽象程度 2抽象 2知识迁移 已有知识的影响，如学校学到的知识及生活中获得的经验等 3知识应用 对商不变性质等知识的直接应用，如模仿或直接代入计算 2任务 1简洁 问卷呈现的不同表征方式的复杂程度 2烦琐 ]

对各个变量的测量指标进行信度分析，直观、抽象、形式表征的cronbach's α系数分别为0.735、0.778、0.785，均大于0.7，问卷具有较好的内部一致性。

三、研究结果

（一）三种表征方式

1. 三种表征方式的得分情况

对教师选择的三种表征的平均分进行统计（见图2），发现教师选择的直观表征的得分最高，抽象表征其次，形式表征得分最低。说明教师认为直观表征对学生来说最容易理解，抽象表征比较容易理解，形式表征最不容易理解。

图2   三种表征平均分统计图

2.三种表征方式的水平

为了分析教师选择的三种表征的差异性情况，通过傅莱德曼（Friedman）检验分析表征的水平，结果显示三种表征得分具有显著性差异[X2（2）=10.686，p<.05]。成对比较分析显示，教师选择直观表征和抽象表征（[p=0.236]），抽象表征和形式表征（[p=0.450]）均不存在显著性差异，即直观表征和抽象表征、抽象表征和形式表征分别在同一个水平;直观表征和形式表征（[p<.05]）存在显著性差异，即直观表征和形式表征不在同一个水平。

由此可见，教师认为对学生而言，直观表征与形式表征水平相差较大，直观表征与抽象表征、抽象表征与形式表征差距较小。形式表征得分最低，说明形式表征最不容易理解。因此，总体来看，形式表征处于最高理解水平，抽象表征在中等水平，直观表征处于最低理解水平。

（二）不同任务的三种表征方式

1. 不同任务三种表征方式的得分情况

计算每个任务下直观表征、抽象表征、形式表征三种表征的平均分（见图3）。可以看出，在同一模型中，直观表征的得分呈下降的趋势，形式表征的得分呈上升的趋势，而抽象表征的得分一直处于比较平稳的状态。说明同一模型中，随着任务难度增加，教师选择的最容易理解的表征方式由直观表征渐渐转向形式表征。

图3   不同任务三种表征方式的得分情况统计图

2. 不同任务三种表征方式的水平

通过傅莱德曼（Friedman）检验分析每个任务下教师三种表征水平的差异性情况，结果显示，任务1-4和任务7下教师选择三种表征得分具有显著性差异[任务1、2、3、4、7的[X2（2）]值分别为：[44.909，][24.045，6.045，31.955，10.686] ，所有[p<.05]]。任务5和任务6，结果显示保留原假设，表明对于这两个任务，教师选择的三种表征都在同一个水平。

成对比较分析显示，任务2和任务4，三种表征两两均不在同一个水平（所有[p<.05]）。任务1，抽象表征和形式表征（[p=0.057]）在同一个水平，直观表征和抽象表征、形式表征（[p<.05]）均不在同一个水平。任务3，直观表征和抽象表征（[p=0.497]）在同一个水平，形式表征和直观表征、抽象表征（[p<.05]）均不在同一个水平。任务7，直观表征和抽象表征（[p=0.859]）在同一个水平，形式表征和直观表征、抽象表征（[p<.05]）均不在同一个水平。

综上，从任务1到任务3，表征水平由直观表征与另两种表征均不在同一个水平，转变为直观表征与抽象表征在同一水平。说明随着任务越来越难，三种表征之间水平差距逐渐减小。从任务4到任务7同样如此。任务7，形式表征已经处于最低理解水平，说明随着难度增加，教师认为形式表征更利于学生理解。

3. 学习路径

被调查的44名教师中，有43名教师认为可以按照任务1-7的顺序进行教学，只有一位教师认为不可以，但却没有提供新的顺序。有9名教师提供了简化方案。教师提供的简化方案大致是任务1、任务3、任务4、任务6、任务7的顺序，也是按照分数除以整数、整数除以分数、分数除以分数的顺序進行编排。

四、讨论与分析

（一）最容易与最不容易理解的表征方式

以下对教师选择三种表征时给出的理由类型进行分析。将每种理由被提供的次数进行了统计，如图4。

图4   三种表征理由分布图

可以发现大多数教师选择直观表征是因为画图比较直观，清晰明了。选择抽象表征是因为语言解释是学生经常接触到的，利于知识迁移。选择形式表征是因为商不变规律直接应用比较方便，并且一部分教师认为形式表征比较抽象，所以相对直观表征和抽象表征，形式表征比较困难。

（二）不同任务表征方式的变化趋势

随着任务的变化，直观表征的得分越来越低。为深入了解教师选择的理由，选取一位教师的访谈内容，如下（T1表示访谈者，T2表示被访谈教师）：

T1：对于任务5：[1÷23]，你说1除以一个非单位分数虽然直观，但不是整数倍，所以有困难。这是指什么？

T2：反应快的学生，会认识到这个[13]正好是半杯，但是反应慢的就不知道[13]l到底是多少杯。实际上要用[13÷23]，因为一杯是[23]l，[13]l是[23]的一半。这个图让他自己画的话，就困难，这时用图反倒不好理解。

从上述访谈中，可以发现对于分数除以整数的任务，当被除数的分子不能被整数整除时，图形并不好画。直观表征虽然能够清晰地看出问题的答案，但有时在操作过程中难以实施。

抽象表征得分一直变化不大。教师选择抽象表征是因为语言解释是一种常见的方式，所以抽象表征的得分并不会随任务难度不同而发生明显波动。

形式表征得分在同一模型中的得分越来越高。教师认为在前面任务中有所铺垫了，那么商不变规律符合学生知识迁移的思维习惯，更容易理解。所以在后面的任务中才会逐渐选择形式表征，如下面这段访谈记录。

T2：我觉得这三种方法运用于商不变性质一看就知道。因为我是打通来考虑的，从任务1开始为商不变性质做了铺垫，所以说到任务5的时候再用商不变规律就很自然了。

可見形式表征作为一种理解算理的方法，是在学生具备了一定的认知基础后，才比较容易被接受。所以教师在前几个任务中并没有倾向于选择形式表征。

（三）学习路径

教师基本认为可以按照分数除以整数、整数除以分数、分数除以分数的顺序进行教学。教师认为这是“从易到难的顺序”“7个任务的设计比较完善”。学生学过整数除以整数，对除法的理解就是平均分，因此从分数除以整数可以理解为将分数平均分开始，再到整数除以分数、分数除以分数，符合学生认知规律。

五、结论与建议

（一）结论

（1）教师对三种表征方式的选择变化分成两段，呈类似趋势。

在同一模型中，随着任务难度增加，直观表征的平均得分呈下降趋势，形式表征逐渐上升，抽象表征变化不大。教师选择的最容易理解的表征方式从直观表征转向形式表征。

（2）教师选择的最容易理解的表征方式随着任务不同有所不同。

任务1到任务4，教师选择的最容易理解的表征方式是直观表征。从任务5开始渐渐认为形式表征比较容易理解，到任务7认为形式表征最容易理解。所以对于分数除法的教学，并不能选择一种表征方式一以贯之。

（3）7个任务构成的学习路径有其合理性。

任务1-7的教学顺序将教学难点，即分数除法的教学内容进行了合理拆分，引导学生对分数除法的各种情况进行逐一分析、总结、探究，从而降低教学难度，有利于学生的理解。

（二）建议

问卷中提供的任务序列得到了44位被试者的一致认可，说明该任务序列是可行的。而对于不同的任务，可以选择不同的表征方式进行教学。

任务1到任务4中，直观表征和抽象表征得分高于形式表征;建议教师对于完成这些任务，首选直观表征，其次选择抽象表征。

任务5和任务6中，直观表征得分最高;任务5形式表征的得分超越抽象表征。建议教师此时开始铺垫商不变规律，即任务5和任务6选择直观表征，辅之以形式表征解释算理。

任务7，属于分数除以分数，是7个任务中难度最大的。形式表征得分最高。建议教师首选形式表征，辅之以抽象表征解释算理。

参考文献：

[1]王光明，范文贵.《义务教育课程标准（2011年版）》解析与教学指导丛书[·]新版课程标准解析与教学指导（小学数学）[M].北京：北京师范大学出版社，2012.

[2]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[3]葛敏辉. 理解视域下“分数除法”计算教学认知起点的调查分析[J]. 小学数学教师， 2018（3）.

[4]徐斌. 形象支撑 沟通联系 理解本质——六年级上册“分数除法”教材解析与教学建议[J]. 小学数学教育，2015（Z4）：53-56.

[5]H.Wu.The Mis-Education of Mathematics Teachers[J].Notices of the AMS， 2011，Volume 58（3）：372-384.

[6]巩子坤. 有理数运算的理解水平及其教与学的策略研究[D].重庆：西南大学，2006.

[7] Andreas Schulz，Timo Leuders. Learning trajectories towards strategy proficiency in multi-digit division – A latent transition analysis of strategy and error profiles[J]. Learning and Individual Differences，2018.

[8]Hui Jin，Jamie N. Mikeska，Hayat Hokayem，Elia Mavronikolas. Toward coherence in curriculum， instruction， and assessment： A review of learning progression literature[J]. Science Education，2019，103（5）.

[9]巩子坤，卢子苓，靳培英，等.分数除以整数学习路径优化的实证研究[J].小学数学教师，2019（2）：75-81.

[10]李津. 基于学习路径优化的教学设计研究[D].杭州：杭州师范大学，2016.

[11]原登慧，李俊.理解远不止于会计算[J].数学教育学报，2011，20（1）：55-57.

[12]巩子坤.理解视阈下的分数除法课程目标的实证研究[J].教育探索，2010（1）：70-73.

[13]巩子坤.“小数乘法运算”课程目标：基于学生的理解水平[A]. 全国数学教育研究会，2010：9.

[14]巩子坤.学生学习小数乘法的基础研究[J].小学数学教师，2017（10）：66-71.

（杭州师范大学理学院   311121

杭州师范大学经亨颐教师教育学院   311121）