数学教学“滑过”现象及应对策略
2019-01-10季仕健
季仕健

【摘 要】教师过度追求教学过程的顺畅,导致数学知识、思想方法等“滑过”的现象时有发生。通过分析小学数学教学中“滑过”现象的具体成因,给出引领“慢”思考、创设主问题、分层探究、善待生成等“防滑”策略来改进数学教学,促进学生思维生长和发展。
【关键词】小学数学;“滑过”现象;教学;策略
一位青年教师在一次教研活动中上了一节“有趣的乘法计算”(苏教版三年级下册)的公开课,带领学生探索两位数乘两位数的相关规律,之后让学生应用规律进行大量练习。整节课教师注重规律的探索,但自始至终没有引领学生回顾反思探索规律的方法。课后与该教师交流得知:“本节课的教学重点是让学生掌握计算的规律,至于探索规律的方法学生一般都不会说。况且这是一节公开课,我怕引导学生回顾反思探索的方法,教学过程会显得不顺畅……”
“学会思考”是数学教学的核心目标之一。本节课探索计算的规律固然重要,但探索规律的方法“观察、猜想、验证、表达、应用”更为重要。在日常数学课堂,有多少思想方法、活动探索的功能、教学育人的价值等在“学生一般都不会说”“教学过程会显得不顺畅”中“滑过”。由此,关注并探讨数学教学中的“滑过”现象,对于改进小学数学教学具有十分积极的现实意义。
一、小学数学教学“滑过”现象
什么是“滑过”现象,它有怎样的具体表现呢?
(一)“滑过”现象的内涵
“滑过”现象源自英国学者爱德华·德·波诺关于思维训练中“注意滑过”的一个形象的比喻。他说:“当我们驱车从A地到B地欣赏美景时,往往会因为车速太快,忽略了途中更美的C地;由A到B的路越顺畅,C地被忽略的可能性就越大。”[1]数学教学亦是如此。教师在教学核心知识时,如概念的形成、规律的探索、方法的内化、模型的建构等,过度追求教学过程的顺畅,降低思考的难度,减少探索过程的曲折,导致设计的数学活动潜在的探索功能学生没能亲身体验、感悟和深度涉及而“一滑而过”,这样的现象便是数学教学上的“滑过现象”。
(二)“滑过”现象的具体表现
在课堂教学中,“滑过”现象的具体表现形式很多,对其加以归类、概括,笔者认为主要存在以下几个表现形式。
1.任务意识“被加强”
在课堂教学中,教师为了完成既定的教学任务,实施的是预设的教学流程,力求开端“良好”、过程“顺畅”和结束“圆满”,教学过程中一般不提出问题让学生“跳一跳”去摘果子,学生的思考过程完全被教师讲授代替;即使提出一些问题,过强的目标意识导致教师也没有留下足够的时间让学生独立思考和进行实质性交流,只是蜻蜓點水地走个程序。
2.思想方法“被轻视”
数学思想方法很重要,但由于它具有内隐性,难以被考查,教师在平时的教学中重视不够,对一些解题的思想、探究知识的方法缺乏应有的回顾和反思,学生虽得了“鱼”而未获“渔”。
3.探究合作“被异化”
在课堂教学中,我们经常会发现:当教师一要求探究,学生立刻就进入探究状态,讨论热烈。仔细观察还会发现,学生根本不是在合作探讨,而是各自为战,互相不倾听、不分享、不评价,甚至有些组员在趁机闲聊……此时的教师也没有全方位地参与到学生的学习过程中去,导致学习中的很多细节问题被“滑过”。
4.生成资源“被丢弃”
在课堂教学中,有些教师面对课堂上突如其来的且有一定思维价值和探究价值的生成,由于预设不充分,通常采用“这样的方法对不对呢,请同学们课后去思考”或“听而不闻”等方法简单应付而草草收场。
二、数学教学“滑过”现象成因分析
“滑过”现象看似是无意识的正常教学行为,但实际上它是教师教学理念陈旧、学情研判失误和教学机智失策等因素综合作用的必然结果。
(一)儿童主体时空失位
让每个孩子与数学浪漫地相遇,既是童年的需要,又是数学教育的需要。但现实课堂上部分教师按照自己对教学内容的理解组织课堂语言、调控讲解速度,没有留下一定的空间和时间让学生停下来慢慢“欣赏”数学内在的风景。殊不知,学生对崭新的知识需要有个“悟”的过程,教学推进的速度太快,学生的思维就会跟不上,导致新知的深层理解和感悟“滑过”。
(二)问题难度设计失当
《义务教育数学课程标准(2011年版)》(以下简称《课程标准》)指出:“教师教学应该以学生的认知水平和已有的经验为基础。”但在实际教学中,有的教师对学生的认知水平研判失误,导致问题难度设计失当。“问题”是数学教学的“牛鼻子”,抓住了它,方可引领学生进行深度的学习。有的问题设置得太简单,对学生思维的深刻性和发展性培养效果不大,学生不能形成认知冲突,教学过程轻松走过;有的问题设置得太难,又超越学生思维的“最近发展区”,导致学生的思维卡壳,无从思考,最后变成教师自问自答,教学过程匆匆“滑过”。
(三)探究过程思维失质
张奠宙教授认为:“数学教学的有效性关键在于对数学本质的把握、揭示和体验。”但在现实的数学课堂教学中,部分教师追求课堂形式的完美,把知识一再地细化、加工,再通过简单的方式“喂”给学生,学生只要根据设定好的步骤简单地进行合作、操作、实验、讨论,课堂看似热闹,思维却浮于浅表,影响了学生对数学本质的理解,导致探究成了点缀课堂的“花架子”。
(四)教学生成应对失智
没有精心的预设,就没有精彩的生成。有些教师担心课堂的生成会导致教学过程偏离事先预设的“轨道”而完不成教学任务或应对生成的智慧不足,出现了对学生的生成关注不够、捕捉不准确、利用不机智等现象,造成一些富有探索价值的素材、育人资源、生长机会在无形之中悄然“滑过”。
三、数学教学“滑过”现象应对策略
有效防止“滑过现象”的产生和蔓延,需要教师思想上确立“防滑”意识,理性思考多维度的“防滑”策略,使学生学会思考、获得经验、自由生长。
(一)引领“慢”思考彰显理性精彩
史宁中教授曾呼吁,让学生“长时间地思考一个问题”。长时间地思考一个问题也可以称为“慢”思考。“慢”思考是指教师在教学数学核心知识时,引导学生全面、细致、深入地思考,把问题琢磨透彻,进而深刻理解和掌握所学的数学知识。
例如,苏教版四年级下册“乘法分配律”有这样的一道选择题:
下面哪个算式与99×a+99结果相等?( )
A. 99×(a+1) B. 99×a+1 C. a×(99+1)
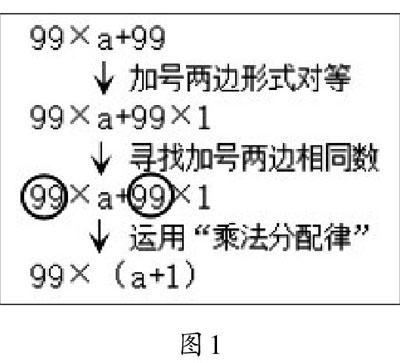
许多学生在解答时选择了C选项。为什么会出现这样群体性错误呢?课后找了几位做错同学进行访谈发现:他们都是凭主观意愿让99+1凑成整百,这样计算就简便了。如果我们引领学生把思考进行分层(如图1),展开“慢”思考,先以线性模式割裂,再一段一段加以比对关联,学生就会很容易发现应选A。在这样的“慢”思考中,教师对知识本质没有急于点破,而是留给学生足够思考的时间和空间,引导学生自主感悟,获得知识,体验成功,对乘法分配律模型的理解能更好地从感性直觉走向理性分析,过程清晰,思维深入。
图1
(二)创设主问题引领思维深刻
美国数学家哈尔莫斯说过:“问题是数学的心脏。”好问题能促使学生主动地去观察、猜想、研究、探索、验证,并激发学生思维的火花、激起学生思辨的冲动,让学生的数学学习真正发生。
例如,在教学苏教版四年级下册“积的变化规律”一课时,设计了三个主问题贯穿全课:第一个问题,以算式20×3=60为例,思考是否存在“一个因数不变,另一个因数乘几,现在的积就等于原来的积乘几”的规律。第二个问题,在20×3这个算式中发现了积的变化现象,那么在其他乘法算式中是不是也存在着相同的变化规律呢?第三个问题,回顾刚才的探索过程,你有什么收获?三个问题逐层逼近知识和方法的内核。第一个问题引发学生研究和探索规律的愿望,促使学生以饱满的热情投入规律探索过程中,但规律的探索必须经历从特殊走向一般,于是提出第二个问题列举一些不同的算式进行验证,进一步丰富学生对规律的感知,再引导学生回顾反思探索过程,并谈收获。整个过程,学生获得的不是简单意义上的“规律”,而是探索数学规律的一般方法,积累了思维活动经验,感悟了不完全归纳的思想,思维走向了深刻。
(三)分层探究揭示核心的概念
在数学教学活动中,教师应激发学生的学习积极性,向学生提供充分从事数学探究活动的机会,帮助他们在自主探究和合作交流的过程中真正理解和掌握基本的数学知识与技能,数学思维和方法,获得广泛的数学活动经验。正如《课程标准》指出:“教学中注意结合具体的学习内容,设计有效的数学探究活动,使学生经历数学的发生发展过程,是学生积累数学活动经验的重要途径。”
例如,在教学苏教版五年级下册“分数的基本性质”一课时,如果教师直接告诉学生[12]=[24]=[48],再引导学生观察分数的分子和分母是如何变化的,从而总结出分数的基本性质,这不是真正意义上的探究。教学这一内容时,笔者设计了三个不同层次的探究活动:第一个层次,首先出示三个分数[12],[24],[48],引导学生猜想验证“它们相等吗,怎样尝试说明?”学生在折一折、算一算、画一画、摆一摆等方法中初步感受分数中的“变与不变”;第二个层次,引导学生找一找生活中像这样的分子分母不同,大小却相等的分数(分西瓜、班级座位分组等),学生再次验证分数的分子和分母变化,分数的大小可能不变;第三个层次,引导学生仔细观察上面得到的等式,总结规律。在这样的三个不同的探究活动中,学生对“分数的基本性质”这一核心概念“知其然并知其所以然”,观察、分析、比较、归纳、概括及动手实践的能力得到培养,思维得到发展,在理解分数的变化规律的同时,还初步体会了“变”与“不变”的辩证思想。
(四)善待生成点燃思维的火花
生成是数学课堂客观存在的。面对学生课堂上的“异想天开”,教师不能浇“一盆冷水”,而要“火上浇油”,这样学生的思维火花才会越烧越旺,潜能和才华才能充分释放。这就要求教师必须深入钻研教材,弄清知识的来龙去脉, 把握学生的认知水平,对课堂有充分的预设。
例如,在教学苏教版五年级上册“三角形面积的计算”一课时,学生运用公式计算底是12米、高是9米的三角形土地面积时,一位同学的列式为12÷2×9=54(平方米)。介绍思路时表示这样计算更简便,而其他同学根据现有的认知经验都认为是错的,原因是12÷2講不出道理。是啊,数学是讲道理的,面对这个突如其来的课堂生成,怎么办?教师灵机一动,顺势介绍了我国古代数学名著《九章算术》中记载的三角形面积的计算方法“半广以乘正从”(“广”指三角形的底,“从”指三角形的高),也就是用三角形底的一半乘三角形的高(如图2)。同时还借助于教学光盘上的动画,采用著名数学家刘徽“以盈补虚”的方法加以说明。学生听后发出“原来如此”的惊叹,对“做错”的那位同学报以热烈的掌声。如果教师担心教学任务完不成而简单地应付“这种方法到底对不对呢?请同学们课后自己上网搜索或查阅资料”,那么,学生对三角形面积的深刻理解和对古人的智慧产生的情感共鸣势必会被“一滑而过”。
总之,“防滑”没有一个固定的模式,也不是一朝一夕可以做到的。但只要教师能在教学中以“儿童为中心”,转变教学观念,改变教学方式,不断积累“防滑”经验,就能让学生的思维得到锻炼、能力得到发展、情感得到共鸣。
参考资料:
[1]爱德华·德·波诺.超级思考帽:爱德华·德·波诺思维训练最新教程[M].陈荣平,译.北京:人民邮电出版社,2006.
(江苏省建湖县实验小学东校区 224700)
