典型红砂岩的蠕变特性研究

王淑豪 ，林晓艺 ，纪海艳 ，王俊杰 ，叶晨暄 ，刘纪峰 ，2

（1．三明学院 建筑工程学院，福建 三明 365004；2．工程材料与结构加固福建省高等学校重点实验室（三明学院），福建 三明365004）

岩石的蠕变是其流变性质中的一种，岩石流变性是指岩石在外界荷载、温度、辐射等条件下呈现的与时间有关的变形、流动和破坏等性质，即时间效应。其主要表现在弹性后效、蠕变、松弛、应变率效应、时效强度和流变损伤断裂等方面[1]。岩石流变是边坡变形失稳的重要原因之一。朱定华[2]通过试验得到红层软岩的长期强度约是单轴抗压强度的63%～70%；刘纪峰等[3-6]的研究表明，水的影响导致岩土体微细结构及成分变化是其变形破坏的主要因素之一；钟雨奕等[7]研究得出成仁高速文宫连接线边坡在开挖和降雨的影响下破坏机制为蠕滑-拉裂；杨旭等[8]采用相似模型，研究了华南巨厚红层在不同降雨模式下的灾变过程和规律；邱恩喜等[9]通过对野外资料的调查分析，得出对边坡稳定性的影响因素依次为为泊松比、弹性模量、坡高和岩体块度；肖尚德等[10]分析了恩施盆地红层边坡变形破坏模式，按影响因素将边坡变形破坏划分为软硬互层红砂岩差异风化、顺层结构面和切层结构面不利组合以及人工开挖扰动3种；叶世斌[11]研究得出结构面是影响川渝地区红层软岩路堑边坡稳定性的关键因素，水的浸润与软化是影响其稳定性的主要因素。

由前人的研究可知，对于红层岩土流变性的研究可对其边坡稳定性预控等工程问题提供借鉴，显得颇为重要。本研究对典型红砂岩试样进行蠕变试验，并通过选用合适的蠕变元件模型得到了其适用的蠕变本构方程。

1 蠕变模型选取

开尔文-伏尔特(Kelvin-Voigt)模型又称广义开尔文模型或中村模型，它是一种线性粘弹性体模型，由一个弹簧和一个开尔文模型串联而成，其结构形式如图1（a）所示[1]。总应变为：

瞬时弹性应变为：

开尔文体应变为：

整理式(1）～(3)可得开尔文-伏尔特模型的本构方程：

当 t＝0 时，施加常应力 σ=σ0，则。由该初始条件，积分式(4)，得：

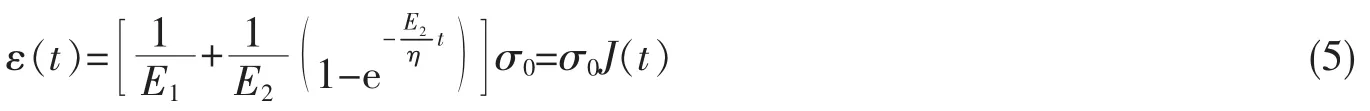
当 t＝0 时，施加常应变 ε＝ε0， 这时ε.＝0，则解本构方程(4),得：

当 t→∞ 时，由式(5)得

因此，开尔文-伏尔特模型的蠕变范围为：

如图1（b）所示，在t=0时刻，施加突然荷载σ0，在加载瞬间产生瞬时应变，并且随着时间的发展，总的应变逐渐增大，最大的极限值为两个弹簧最大应变的总和，并保持该荷载不变到t=tl。当在该时刻卸去该荷载，其模型的应变如图1（b）所示t1时刻后的蠕变曲线：在卸载的瞬间，应变会发生一部分瞬时弹性恢复，而且还有一部分会随时间的发展而逐渐恢复，直至最后恢复为零。

图1 开尔文-伏尔特模型及其蠕变曲线

2 红层岩样的蠕变试验验证

蠕变试验的加载方式通常有分别加载、分级增量加载、分级增量循环加卸载3种方式。分别加载，就是对同一种岩土样需要取得完全相同的试样若干，在相同的试验条件和不同的应力水平下进行试验，得到一簇不同应力水平下的蠕变全过程曲线，如图2（a）所示。这种方法从理论上说最符合蠕变试验所需要的条件，而且能直接反映岩土的蠕变全过程。但真正做到严格的分别加载是不容易的，一方面保证上述完全相同的试验条件不太可能；另一方面很难有这么多套的仪器设备同时来做长时间的蠕变试验。所以目前国内外的室内蠕变试验一般不采用这种方法，而是常采用分级加载的办法。

分级加载，就是在同一试样上逐级加上不同的应力，即在一级应力水平下蠕变经历给定的时间或达到稳定后，将应力水平提高到下一级的水平，直到所需的应力水平，如图2（b）所示，它的应力水平随时间的变化以及所得到蠕变曲线呈上升的阶梯形曲线。

分级增量循环加卸载方式(如图2（c）)，它吸取了分级增量加载方式的优点，克服了其缺点，试验过程中可观测到试样的滞后弹性恢复，测得其残余变形，故全面地反映了试样蠕变曲线的加卸载过程，能为试样流变力学模型的建立和模型参数的确定提供完整的试验数据，但试验设备要求较高。受此限制，本试验采用分级增量加载方式。

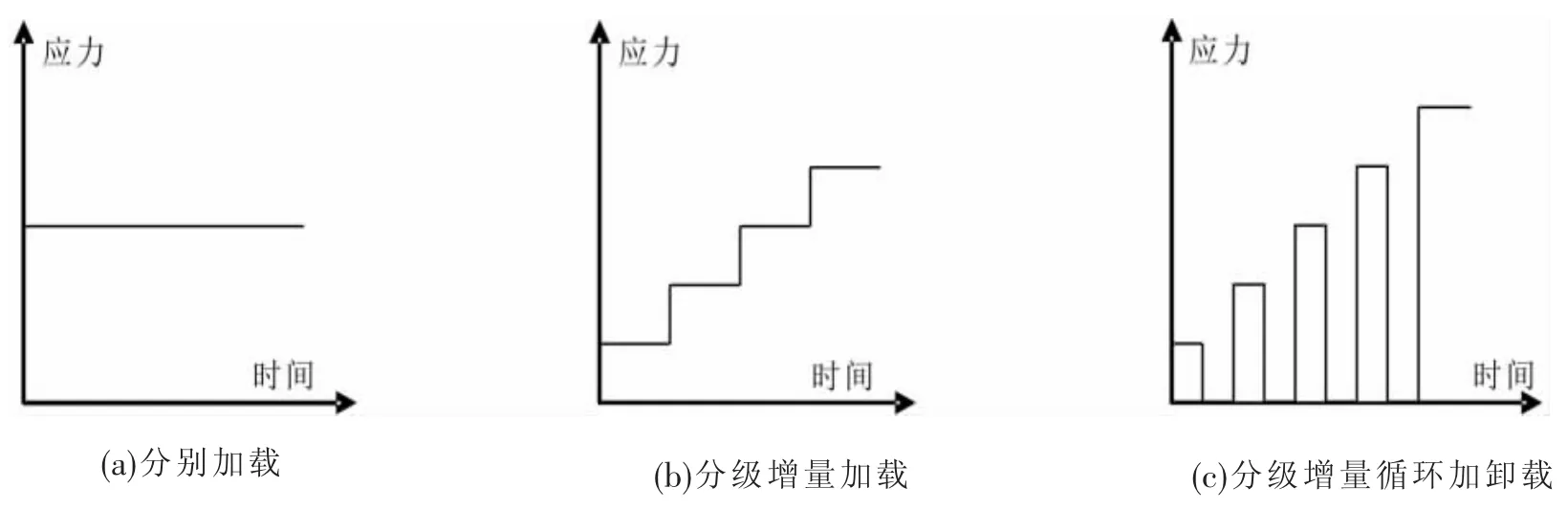
图2 蠕变加载方式示意图

本文试验所用试样为红层典型红砂岩，试样如图3所示。试验步骤如下；试样加工成直径61.8 mm，高130 mm的圆柱体，打磨，贴应变片，将导线焊牢，在应变片、端子及其与导线的接头的外表面粘贴914胶水，待胶水阴干后，将导线的另一端按要求连接到转换箱，设置数据采集仪及其配套软件的相关参数。确认设置无误后，即可操作油压控制台，将试样平放在的试样承载台上，在试样的上表面放置荷重传感器，开始缓慢的送油压，让油泵下表面接触到荷重传感器，则可以开始分级增量加载的蠕变试验，数据采集仪自动采集数据。本试验分三级加载，依次为：8、16和24 MPa，每级荷载持续时间 144 h（6 d），累积加载 18 d。

将采集到的数据用Origin6.1处理得到图4所示曲线。

图3 典型红砂岩蠕变试验岩样

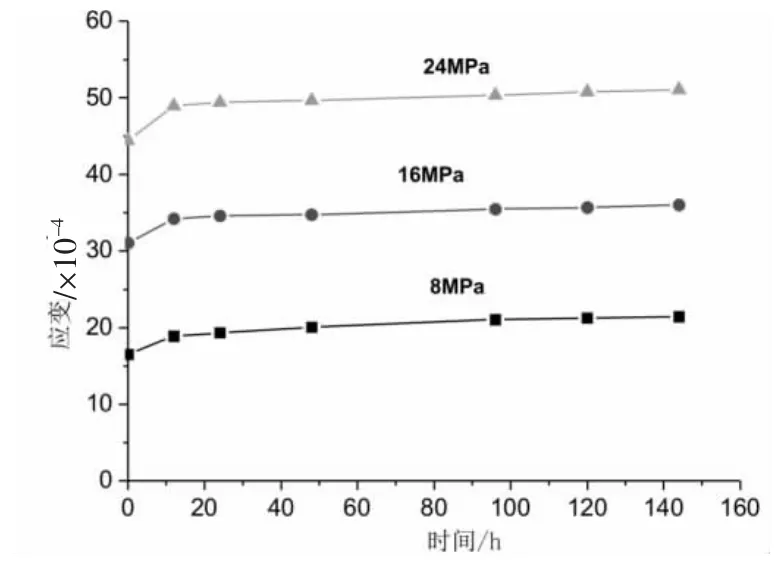
图4 典型红砂岩单轴压缩蠕变试验曲线

3 典型红砂岩蠕变模型的确定

由试验曲线特征，蠕变方程式（4）等价于：

运用最小二乘法进行蠕变元件组合模型参数的辨识[12-13]。令

则式(9)可化为：

运用Origin软件进行自定义非线性函数拟合，自定义非线性函数即为式(13)。

当 σ0＝8 MPa 时，拟合得到：

P1=0.002 15±0.000 03,P2=3 782.545 91±162.766 57，P3=47 270.311 19±1 195.487 95

同理可以得到：

当 σ0＝16 MPa 时，

P1=0.002 22±0.000 02,P2=3 653.738 09±457.751 79， P3=44 909.950 54±14 888.127 23

当 σ0＝24MPa 时，

P1=0.002 1±0.000 01,P2=4 030.980 98±431.167 04，P3=41 073.9712±12 038.692 48

为方便对比分析，以上数据填入表1。

从表1可以看出：P1，P2，P3各自在3种不同的应力水平下的取值都有一定的差别。但是，通过仔细观察可以发现：

（1）P1在各个应力水平下的取值相当接近，误差量级为1×10-4，可以考虑取它们的平均值。

表1 不同应力水平下求得的定常参数(P1,P2,P3)及最小二乘误差(f)

（2）P2和P3在3个应力水平下各自的误差允许范围内有重叠的数值区间，经计算确认：P2的重叠区间为 3 619.779～3 945.312 48，P3的重叠区间为 35 316.823 24～53 112.663 68。然后求出，最后把前者作为最终取值，把后者作为误差取值范围。

经计算得到相应的结果，结果见表2。

表2 定常参数(P1,P2,P3)取值的分析表

因此定常参数的最终取值如下：

将值代入式（13）得铁红砂岩适用的蠕变方程如下：

将 P1，P2，P3各值代入式(10)～(13)得：

将σ0=8，16，24 MPa，分别回代到（14）中，得不同应力水平下的蠕变方程依次为：

如图5所示，三个应力水平下的拟合曲线与试验结果对比发现：16 MPa的曲线与试验点非常接近，8和24 MPa的拟合曲线与试验点离得较远。究其原因，主要是元件组合模型得到的流变方程得到的各个时刻的本构关系本身是线性的，而蠕变试验结果表现的实际情况是非线性的[14]，如图6～7，这就是元件模型本身的局限性，图6～7中典型红砂岩单轴压缩的蠕变的等时曲线得到的7个时刻的应力应变本构关系曲线都不是直线，因此，如需较好的拟合试验曲线，必须用非线性的元件模型。限于篇幅，本文在此不做探讨。

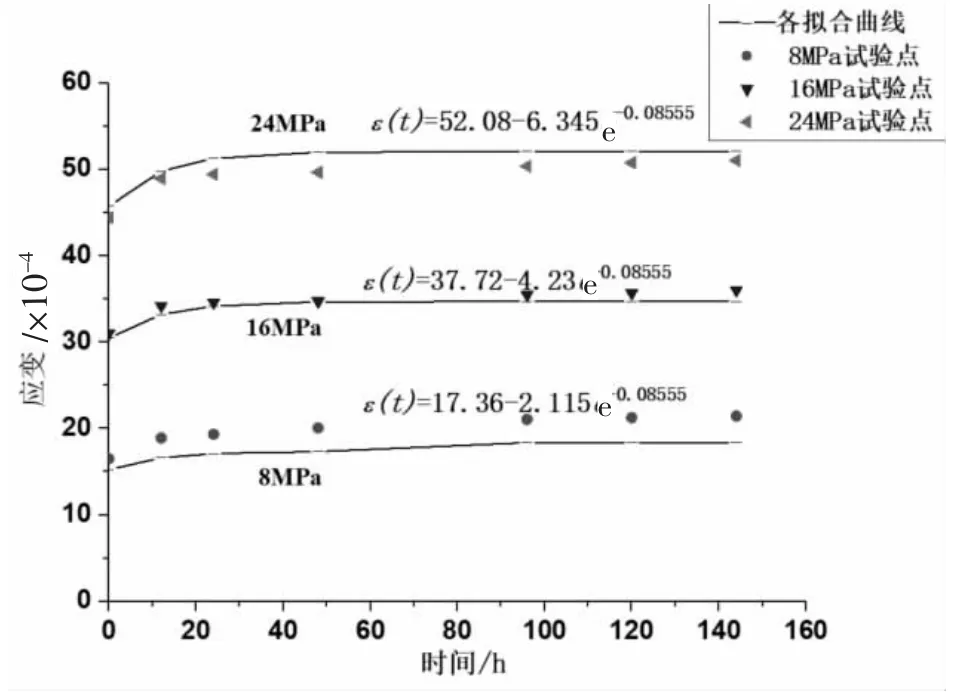
图5 典型红砂岩单轴压缩蠕变拟合曲线和试验点对照图

图6 典型红砂岩单轴压缩蠕变等时曲线

图7 典型红砂岩单轴压缩蠕变等时曲线局部放大图

4 结论

岩石流变是边坡变形失稳的重要原因之一，对于典型红砂岩蠕变特性的研究可对其边坡稳定性预控等工程问题提供借鉴。本文对典型红砂岩试样进行了单轴压缩蠕变试验。试验获取了典型红砂岩的应力-应变关系及其随时间变化的特性，通过选用元件组合的开尔文-伏尔特模型进行数据拟合，得到式（14）所示的红砂岩通用的蠕变本构方程。该结果可为深入研究含典型红砂岩条件的滑坡等地质灾害预防和较好的解决岩体蠕变损失等问题提供参考借鉴。