区间估计和假设检验的特点及应用

李帅

(河南师范大学，河南 新乡 453000)

1 区间估计和假设检验的特点

1.1 区间估计

区间估计是数理统计中的重要的一部分，深刻地掌握和灵活地运用区间估计的思想方法对于解决实际问题起着举足轻重的作用。区间估计是以一定的误差和概率对总体参数进行估计的方法。本文着重研究区间估计对总体均值的估计。

当样本容量较大时，由中心极限定理得，样本均值经过标准化后服从标准正态分布，当总体标准差σ已知时，可以使用总体标准差；当标准差σ未知时，可以使用样本标准差s来代替，由此可以构建一个正态分布总体均值在置信水平1-α下的置信区间。

例 设y1,y2,y3,…,y9是来自N(μ,σ2)的样本，则μ的置信水平为1-α的置信区间为

1.2 假设检验

接下来，我们对用于参数推断估计的另一种方法假设检验进行研究。假设检验的思想方法和区间估计的思想方法有一些相似之处，两者是相互贯通的，有着密切的联系。假设检验根据假设的提出可以将其分为双侧检验，左侧检验和右侧检验：(1)双侧检验：H0：μ=μ0;H1：μ≠μ0;(2)左侧检验：;(3)右侧检验：。在进行假设检验时，通常情况下，人们可以根据统计量或P值进行决策，以下我们在总体服从正态分布的情况下，探讨两者的区别和联系。

i)用统计量决策

ii)用P值决策

在利用统计量做决策时，如果给定显著性水平α的大小，只需计算出样本统计量值的值大小，观察其是否落入拒绝域。这样，无论样本统计量的大小，只要其落入拒绝域，我们就拒绝原假设，导致我们无法知道犯错误的真实概率。而利用P值决策，我们通过计算样本统计量的概率大小，从而掌握了决策犯错误的概率。

无论我们采用统计量决策还是P值决策，都有可能犯错误。可能犯的错误分为两种，即第一类错误和第二类错误，概率大小分别为α和β。通常情况下，记，。在样本量不变的情况下，要减少α必然导致β的增大，而减少β的大小必然导致α的增大。根据正态分布曲线的特点，当样本的方差越小，数据分布越集中的特点得，增大样本容量，可同时减小α和β。

2 区间估计和假设检验的实例探讨

区间估计和假设检验在解决实际问题中有广泛地用途，本文以下部分分别针对区间估计和假设检验的实际应用进行探讨。

例 为研究某种汽车轮胎的磨损特性，随机地选择18只轮胎，每只轮胎行驶到磨坏为止，记录所行驶的路程(以Km计)如下表：

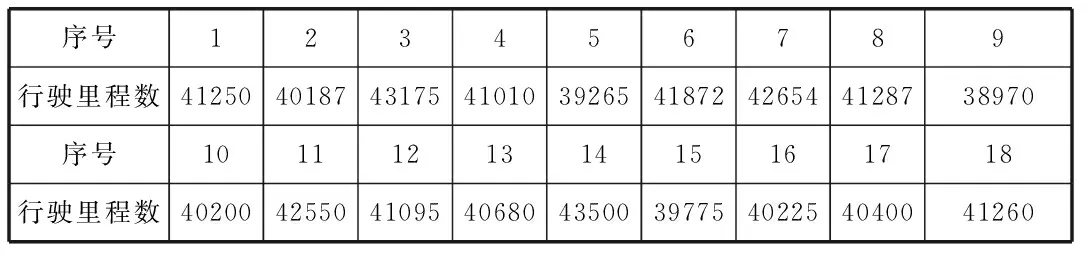
表1 汽车轮胎的行驶里程数

假设这些数据来自正态总体N(μ,σ2)，其中μ，σ2未知，试求μ的置信水平为0.95的置信区间。

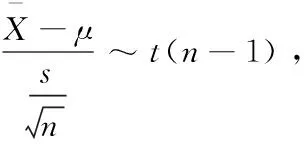
=(40455.12,41695.44)

例 一种机床加工的零件尺寸绝对平均误差为1.35毫米。生产厂家现采用一种新的机床进行加工以期进一步降低误差。为检验新机床加工的零件平均误差与旧机床相比是否有显著降低，从某天生产的零件中随机抽取50个进行检验。50个零件尺寸的绝对误差数据见表2

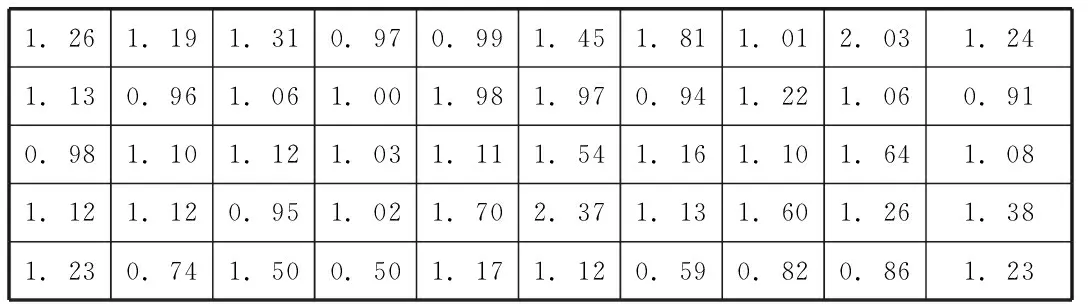
表2 50个零件的绝对误差(单位：mm)

利用这些样本数据，检验新机床加工的零件尺寸的平均误差与旧机床相比是否有显著降低(α=0.01)。

解 由题意，我们需要检验的假设为：

H0：μ≥1.35;H1：μ<1.35

由此拒绝原假设。

3 总结

通过上述对区间估计和假设检验的分析和实际应用，我们可以体会到两者之间存在一定的联系。一般情况下，区间估计与假设检验可以相互转换。置信区间与接受域对应，置信水平1-α与显著性水平α对应。但两者也有区别：区间估计是对给定的样本，构造一个参数取值最合理的范围(置信区间)；假设检验是给定参数值(原假设)，确定哪些样本值(拒绝域)与参数值不一致。