椭圆形封头旋压成形过程数值模拟与分析

田文爽，孙卫国

(1. 中国海洋石油集团有限公司节能减排监测中心，天津 300452； 2. 艾西斯腾德国有限公司，德国 慕尼黑 80331-81929)

由于化工装置规模不断扩大，工艺设备逐渐呈现大型化的趋势。传统的封头冲压成形技术在大型封头生产中遇到了很多困难。旋压成形技术以其独特的优点，已成为大型封头的重要生产手段，国内外对封头旋压成形工艺的研究也不断深入【1】。随着科学技术的飞速发展，封头旋压成形工艺的数值模拟研究得到了迅速发展并提高到了一个新的阶段。

林波等人【2】提出两模法和两轮法的旋压成形试验方案，并设计不同旋压试验方案的芯模和旋轮工装，提出了两轮法旋压超半球壳体的多道次拉深旋压成形工艺。刘兴家等人【3】建立了成形过程中各道次旋轮运动轨迹控制参数间的递推关系， 求得各道次旋轮轨迹的控制参数值， 较系统地提出了一种合理分配各道次旋压变形量的方法。Shimizu【4】和 Kawai等人【5】对旋压工艺中一些旋轮的运动问题进行了讨论。这些研究尚未涉及模型计算时间长，旋轮轨迹复杂和回弹严重的问题。

张艳秋等人【6】对薄壁铝合金封头冷旋压成形过程进行了弹塑性有限元数值模拟，揭示了成形时的塑性变形流动规律，并分析了主要工艺参数对成形质量的影响规律及失效问题产生的原因。胡福泰等人【7】用有限元数值计算的方法，合理确定了封头旋压计算的力学模型。张晋辉等人【8】建立了锥形件剪切旋压的三维有限元模型，进而获得了偏离率、旋轮圆角半径、旋轮进给量、芯模转速及旋轮直径对LY12M锥形件剪切旋压力和壁厚差的影响规律。李文平等人【9】建立了碟形封头冷旋压的三维有限元数学模型，分析了封头在冷旋压成形过程中应力应变的分布规律，计算了旋压力并分析了其变化的原因。

运用数值模拟，可以对金属压力加工过程中金属的流动进行分析，从而得到应力应变分布规律等，进而预测金属变形情况以及对工艺参数进行优化。有限元分析软件方便的操作以及超强的仿真性促进了数值模拟技术在锻造和旋压等行业中的广泛应用【10】，在保证工件质量、减少材料消耗、提高生产效率、缩短试制周期方面显示出无可比拟的优越性。本文基于ANSYS/LS-DYNA有限元分析软件，建立了封头旋压成形的三维有限元模型，利用有限元模型，对封头成形过程中的应力场、应变场的变化进行分析，为封头旋压成形实际生产提供了可靠参考。

1 大变形成形理论基础

1.1 大变形动力学数值计算方法

在实际工程中，经常会遇到几何大变形问题，例如板壳结构的大挠度、屈曲和过屈曲问题等，这时需要使用大变形条件下的应力与应变度量。

对于与变形历史不相关的弹性大变形问题可以采用全量方法研究【11】，也就是直接求已知载荷与约束作用下的结构变形与应变、应力。将变形前的构形作为参考构形，变形后的构形及相应的应变、应力作为待求量，采用牛顿法、拟牛顿法等方法进行迭代【12】。

对与变形历史有关的大变形问题，如材料粘弹性模型以及惯性等时间效应，必须采用增量方法，即将时间变量离散成某个时间序列：t0=0,t1,t2,…,tn,tn+1，然后求这些离散时间点上的数值解。求解方法依参考构形选择的不同可以分为更新拉格朗日格式(U.L.)以及完全拉格朗日格式(T.L.)【13】。更新拉格朗日格式在计算[t,t+Δt]区间的所有变量时，以t时刻的构形作为参考，应力、应变描述主要采用Euler应力和关于现时构形的无限小应变；完全拉格朗日以t0=0时刻的构形作为参考构形，应力、应变描述主要采用Kirchhoff应力和关于初始构形定义的Green应变【14】。

1.2 大变形动力学有限元基本解法与求解过程

求解弹性动力学振动响应主要有以下3类方法：时域方法、频域方法和响应谱方法。其中时域方法根据解法的不同又可以分为直接积分法、模态叠加法与状态空间法。直接积分法又可以分为中心差分法、Houbolt法、Wilsonθ法以及Newmark法等。中心差分法是LS-DYNA所采用的主要算法，在求解时，假定t0=0,t1,t2,…,tn时刻的节点位移、速度与加速度均为已知，求解tn+1(t+Δt)时刻的结构响应【15】。

2 标准椭圆形封头有限元模型的简化及参数确定

2.1 封头有限元模型的建立

由于封头旋压成形过程比较复杂，影响因素较多，在数值模拟中，为了能够建立描述其成形过程的有限元模型，有必要对实际加工过程做出合理的简化。在模型中，旋压辊与成形辊设为刚性体，并简化为2个直径相同的球壳。板坯预压成形部分为刚体， 需要旋压部分为变形体， 变形体部分简化为圆锥面， 与预压件刚体部分末端相切。预压件刚体部分绕中心轴线转动， 旋压辊和成形辊在所在平面内做平面运动。为了使模拟条件与真实情况一致， 模型的工艺参数均与实际工作参数相同。考虑是冷成形过程， 忽略温度变化的影响。

标准椭圆形封头尺寸通过查阅JB/T 4729—1994确定，选择直径为φ2 000 mm，厚度16 mm，直边部分40 mm的封头作为研究对象。板坯材料选用为Q345R，材料性质见表1。板坯预压件采用shell163单元，预压件的尺寸应用周长法，通过MATLAB程序确定，LS-DYNA中建模需要的点的坐标也通过MATLAB程序计算得到。板坯预压件绕中心轴线旋转的速度取75 r/min。旋压辊和成形辊的直径均设为φ0.2 m。为了提高计算效率，旋压辊和成形辊均采用shell163单元，厚度设为5 mm，摩擦系数取0.25。

表1 封头材料参数

在模型中，所有单元均采用四面体划分网格，为了提高计算精度，同时控制计算时间，旋压辊和成形辊的单元尺寸设为0.1，板坯的单元尺寸设为0.05。最终建立的模型及网格划分如图1所示。

图1 封头旋压成形有限元模型及网格划分示意

2.2 旋压成形旋轮轨迹的确定

椭圆封头由椭圆部分和直边部分组成，旋压成形工艺中两部分要分别旋制而成，建立封头旋压成形工艺有限元模型的关键在于给出精确的旋轮运动轨迹。在模型中，毛坯旋转的同时，成形辊和旋压辊按照给定的运动轨迹运动，使板坯变形，逐渐成为所要加工的形状。

对图1模型，为了能正确地模拟结构的响应，必须定义与指定时间间隔相对应的载荷，所以在ANSYS/LS-DYNA中用一对数组参数定义载荷：一个定义时间，另一个定义载荷。

与时间数组相对应的是板坯旋转的角速度数组，应用MATLAB程序计算确定旋压辊和成形辊在x方向和y方向运动的位移数组。由于旋压过程中，毛坯绕主轴转动，故旋轮只需做平面运动。图2为旋轮在旋制封头椭圆部分时，在运动平面上轨迹的示意图，因为旋压模型是对称结构，所以取其中的一半进行计算并输出旋压辊和成形辊位移数组数据。

图2 旋轮轨迹计算示意

3 椭圆形封头旋压成形数值模拟结果的分析

3.1 旋压成形数值模拟结果

将数组计算结果导入ANSYS/LS-DYNA，并将载荷分别施加到相应的part上。程序的计算时间根据旋轮的转速和旋轮进给比确定，并体现在时间数组里，载荷加载完成之后对模型进行求解并得到结果。

图3显示的是在经过600 s过程结束时的成形示意图，从中可以看出，通过数值计算的手段，实现了封头从旋压初始毛坯结构到实际产品的成形，数值计算的最终几何结构接近于实际标准椭圆形封头结构，表明本文所开发的三维椭圆形封头旋压成形过程的有限元数值模型具有一定的可行性和可靠性。另外，从图3中可以看到封头成形的直边段出现褶皱，这是封头成形过程存在的一种主要缺陷形式，需要理论研究者或者实际操作者慎重考虑，并尽力避免褶皱缺陷生成或限制其在合理的范围内。

图3 旋压成形数值模拟结果示意

3.2 封头旋压成形应力、应变场分布

封头旋压成形过程中4个不同时期的Mises等效应力云图如图4所示。由图4可以看出，等效应力最大值总是出现在旋压辊作用点附近的区域内，由于本模型选用理想弹塑性材料，最大等效应力为345 MPa，因此一旦材料等效应力达到该值，金属应力将不再增加，而主要体现在塑性变形。同时，随着变形量的变大，等效应力达到最大值的区域范围越来越大，这是因为此时发生了更为剧烈的塑性变形。

图4 不同阶段mises等效应力云图

封头旋压成形过程中不同时期的等效塑性应变如图5所示，不同于等效应力云图，等效应变云图反映的是结构的变形行为。由图5可以看出，在旋压成形的初始阶段，也就是成形过程的小变形阶段，等效塑性应变很小，包含的区域也很小，随后的几个阶段，即成形过程的大变形阶段和直边成形阶段，毛坯的塑性变形较大，等效塑性应变逐渐增大，云图包含的区域也逐渐增大。

3.3 封头旋压成形厚度减薄率变化分布

封头厚度减薄率是封头成形质量控制的一个非常重要的指标，封头旋压成形过程中不同阶段毛坯厚度的分布云图如图6所示。

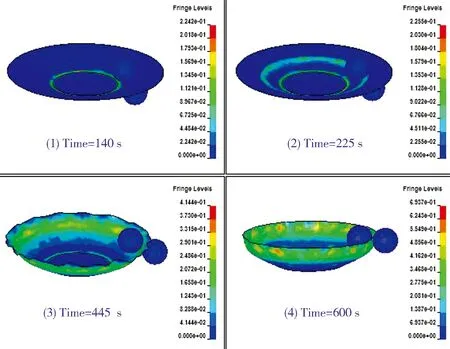
图5 不同阶段塑性等效应变分布云图

图6 不同时刻封头厚度减薄率分布

由图6可以看出，在旋压初始阶段，毛坯厚度没有显著变化。随着旋压成形的进行，厚度减薄率峰值逐渐增加，成形中期出现减薄率最大部位。如在225 s时，最大厚度减薄率为3.05%，而在445 s时，最大厚度减薄率为11.82%，表明在该段时间内，塑性变形较为剧烈，最大厚度减薄率增加较快。在600 s时，最大厚度减薄率峰值11.86%，且位置与445 s 时相比不再进一步变化，说明剧烈塑性变形阶段之后变形过程趋缓，成形过程厚度减薄率不再继续增加。

整个成形过程，最大厚度减薄率11.86%，满足GB/T 25198—2010附录J中对DN 2000、名义厚度16 mm的椭圆形封头厚度减薄率不超过13%的要求【16】。

3.4 封头褶皱形成分析

封头直边段某节点速度的时间历程曲线如图7 所示。由图7可以看出，在旋压成形400 s以前，速度趋于稳定，但超过400 s以后，该节点速度出现一定的波动。在宏观上表现为此时结构端部，即直边段发生了褶皱，从而引起速度的变化。可见在封头成形后半部分，封头毛坯的金属流动过程复杂，易产生褶皱。同时也可以看出，随着旋压过程的结束，褶皱现象明显减少，并逐渐趋于平稳。

图7 封头直边段某节点速度的时间历程曲线

4 结语

1) 根据旋压机的工作原理，结合生产实际，利用几何方法求出封头旋压成形工艺中旋轮运动轨迹的计算公式。采用MATLAB程序实现了旋轮轨迹的计算，并实现了与ANSYS/LS-DYNA软件的对接， 为应用数值模拟的方法研究封头旋压成形工艺提供了有效的改进方法和可靠的依据。

2) 基于ANSYS/LS-DYNA有限元分析软件，应用MATLAB程序得到的旋轮轨迹，建立了封头旋压成形的三维有限元模型，对模型进行了合理简化。利用有限元模型，对封头成形过程中的应力场、应变场进行了分析，得到了封头旋压过程中不同阶段的应力场、应变场分布规律以及封头壁厚的变化规律。

3) 由数值分析结果可知，等效应力最大值出现在旋压辊作用点附近的区域内，并且随着变形量的增大，等效应力最大值所在区域的范围也越来越大；在旋压成形过程中，随着变形量的增大，等效塑性应变逐渐增大，变形区域也逐渐增大；在旋压初始阶段，毛坯厚度减薄率较低，及至发生剧烈塑性变形的阶段，毛坯的厚度减薄率逐渐增大并达到峰值，本文设置的参数下，减薄率能够控制在12%以内，符合相关标准要求。