粒子群优化算法进展研究

吴玫

（江苏城乡建设职业学院，江苏 常州 213002）

1 引言

粒子群优化算法由Eberhart博士和Kennedy博士提出[1]，是一种源于对鸟群捕食行为的研究而发明的进化计算技术，后来演化为一种简单有效的优化计算技术，也是EA中一项新发展起来的技术。由于对粒子群优化算法的研究时间较短，尚缺乏理论基础，一些参数也需要根据具体问题依经验而定，更多深入细致的工作还有待进一步展开。

2 粒子群优化算法的改进

粒子群算法计算形式简单，参数设置少且算法收敛性良好，被应用到各个领域。但在应用的过程中，发现粒子群算法易陷入局部，得不到最优解且收敛速度慢[2]，因此，各种改进的粒子群优化算法被相继研究如何提高粒子群的求解性能和速度。

2.1 算法参数的改进

粒子群算法中的参数很多，其中，粒子种群大小M，粒子的最大速度Vmax等可以采用数值实验的方法来确定大致范围，而惯性权重W和加速常数C1、C2粒子运行的轨迹有着直接的影响，因此，算法的效果与这几个参数有着更直接的关系[3]。

2.1.1 改进参数惯性权重W

粒子群优化算法是以种群行为来激励粒子的运动。每个潜在的解与粒子的速度有关，为使粒子朝着更好的方向发展，需要不断地根据粒子与邻居粒子的经验来调整。

目前对W参数较典型的改进主要有[4]：

①线性调整W：随着迭代的进行，线性减少W的值。根据公式

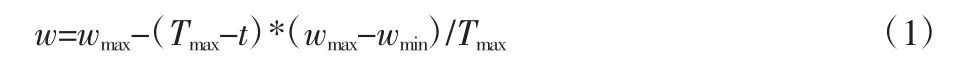
计算，使粒子在初期能较快更新搜索区域，搜索到较大的解空间，从而加快收敛速度。

②非线性调整W：根据相应规则来动态调整W，如一种模糊规则动态调整W的算法[5]，该算法是通过隶属度函数和模糊规则来确定惯性权重的增量，根据当前最好性能评价，但此方法实现困难，需要专家知识建立模糊规则，计算较复杂。

③随机选取W：随机选取的W值，其数学期望值会根据最优解的变化而自适应地调节，因为随机的W值会使粒子的历史速度随机的影响当前的速度。惯性权重的变化由粒子群的进化速度和聚集度综合决定，受算法运行态势的影响，因而能提高收敛速度和精度。

2.1.2 改进加速常数C1、C2

加速常数C1、C2代表了粒子的随机加速权值。通过实验取非对称的 C1、C2的变化范围，发现 C1取 2.75～1.25，C2取 0.50～2.25时，大多数的基准函数都可以获得相对较好的适应值。

2.1.3 改进进化公式

主要是更新速度公式。利用个体平均极值取代算法中的个体极值，使粒子获得更多其他粒子的有用信息，从而提高收敛稳定性和精度。将全局最优模型与局部最优模型结合得到一种复合模型的算法。速度更新公式为：

其中，c1=2，c2+c3=2。

2.2 拓扑结构的改进

2.2.1 局部版粒子群

粒子群有全局版和局部版两种。与全局版选择整个种群作为粒子邻居不同的是，局部版选择其中一部分作为粒子的邻居，局部极值是所有邻居中的最好解，每个粒子追随个体极值和局部极值。

2.2.2 空间邻域法

“空间邻域法”由Suganthan提出，是一种基于粒子的空间位置划分的方法。在该方法的迭代中，计算每一个粒子与群中其他粒子的距离，任何2个粒子间的最大距离为dmax。如果要计算粒子a的邻居：对每一粒子b按照||Xa-Xb||/dmax计算一个比值，当b满足||Xa-Xb||/dmax

2.2.3 邻域拓扑法

Kennedy等对粒子群的拓扑结构进行了研究，通过分析粒子间的信息流提出了环形、轮形和星形等一系列的改进的拓扑结构。另外还有动态粒子群拓扑结构。

2.2.4 社会趋同法

Kenney提出了社会趋同法，该算法混合了空间邻域和环形拓扑，粒子用聚类中心代替个体极值，能提高算法的性能，但也会增加复杂度。

2.3 混合算法

粒子群优化算法容易早熟收敛、局部寻优能力差，这基本上是所有随机算法都有的弊病，而模拟退火算法、直接搜索法、梯度法、爬山法等一些优化算法却具有很强的局部搜索能力，因此，混合粒子群算法是改进粒子群算法的一个研究方向。

Nocl等人提出了利用梯度信息的混合粒子群算法，使算法搜索到局部最优点，并且节省了比较的计算量，加快了收敛速度。Wachowiak等人提出在粒子群算法中嵌入Powell方法，提高了解的精度。

Shi等人提出将遗传算法与粒子群算法混合，并介绍了两种混合方法：粒子群遗传并行混合进化算法(PGPHEA)和粒子群遗传串行混合进化算法(PGSHEA)。

俞欢军通过对参数进行适当地调节将局部搜索和变异操作同时混合到粒子群算法中，此算法发挥了局部搜索和变异操作的优点。高鹰将模拟退火算法与粒子群算法结合，利用模拟退火较强的跳出局部最优解的能力和粒子群全局寻优能力，实现简单的优点，提高了进化后期算法的收敛速度和精度。

除此，目前还有自适应粒子群算法、带收缩因子的粒子群算法、离散粒子群算法以及协同粒子群、随机粒子群、智能粒子群等改进的粒子群算法。

3 结语

粒子群优化算法是一种新型的演化算法，其概念简单，参数较少，易于实现，自提出以来就被广泛研究与应用。但粒子群算法无论是理论还是实践都尚未成熟，存在随机性强，易陷入局部最优导致收敛慢、精度低等问题。因此，寻求更加有效的粒子群改进算法是很有意义的。近年来，粒子群算法的改进引入了许多新的数学工具，吸收了生物学的最新成果，随着新技术的进步与研究的深入，粒子群算法在操作技术和方法上将更通用、更有效。