基于全相位数据处理的数字电能计量算法
2019-01-09徐宏伟孟展李红斌李鹏程杨沁晖张俊玮
徐宏伟,孟展,李红斌,李鹏程,杨沁晖,张俊玮
(1.贵州电网有限责任公司电力科学研究院,贵阳550000;2.华中科技大学,武汉430074)
0 引 言
在新一代智能变电站中,数字电能表得到了广泛的应用[1],数字化电能表作为数字化电能计量系统的终端计量设备,其计量准确性十分关键。变电站中的电子式互感器或模拟量输入合并单元输出符合IEC 61850-9-2(LE)协议的采样值报文,数字化电能表接收采样值报文进行电能计量。
与传统电能表相比,数字化电能表没有A/D采样模块,结构更为简洁[2-3],一般认为其工作模式类似于计算器,其误差应该很小,甚至为零,但是在实际工程应用中却多次发现有数字化电能表出现误差超差现象,长期计量性能失准。
由于数字化电能表的前端设备A/D采样模块采样率、采样位数等性能显著低于传统电能表,因此数字化电能表内部对波形的还原程度较差。且数字化电能表普遍采用点积和算法[4],仅当输入信号为理想正弦波时,由于信号具有完全对称性,正负半波的计算误差可以相互抵消,点积和算法具有较高计量精度,但是在非稳态情况下其现场适应性难以满足计量要求。目前已有研究提出将高阶数值积分算法应用于数字化电能表[5],但是其本质依旧是将采样点进行累积计算电能,在非理想工况下的适应能力并未得到显著提高。针对这一问题,本文提出了将全相位数据处理方法应用于数字电能计量的新算法,该算法一方面可以根据现场负荷波动自适应调整参与DFT运算的采样点数,将非同步采样转化为近似同步采样,能够有效抑制频谱泄露,另一方面与现有的数字电能算法相比,具有较强的现场适应能力,在复杂负荷的条件下能够准确计量电能。且该算法实现简单,能够直接在DSP芯片上实现,本文基于该算法研制了0.01级标准数字化电能表,通过在实验室与其他厂家数字化电能表对比测试,证明了所提出的数字电能算法能够在复杂负荷条件下准确计量电能,具有较强的现场适应能力。
1 数字电能算法误差影响因素分析
变电站现场负荷时常出现波动,其中一些负荷波动可能对数字化电能表的计量准确性产生明显影响,本文针对采样值报文丢失、频率波动以及频率波动时的谐波影响进行建模分析,得到了传统数字电能算法在这几种工况下的理论误差,并在后续章节中验证了所提出的数字电能算法对以上影响因素的适应能力。
1.1 采样值报文丢失误差
数字化变电站的网络环境复杂,数字化电能表接收到的采样值报文中可能会出现采样值报文丢失的情况[6],可能会导致电能计量出现误差。若数字化电能表检测到采样值报文大量丢失,数字化电能表会将当前工况判断为故障工况,此时进行计量误差分析毫无意义,因此仅分析采样值报文少量丢失情况下数字化电能表的计量误差。
采样值报文中每周期的采样值点数保持不变,发生单个采样值丢失时的有功功率表达式为:
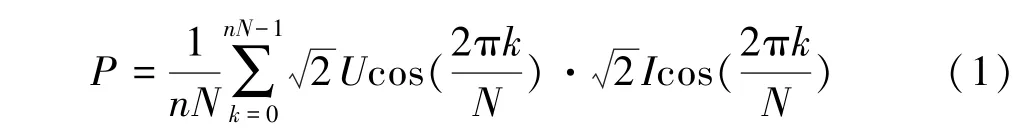
式中n为用于计算电能的报文周期数;N为单周波中的采样点数;i为丢失的数据包编号;k=0,1,2,…。若数字电能算法中未包含插值补偿,则数字化电能表会对丢失的数据包做“填0”处理,此时有功功率误差表达式为:
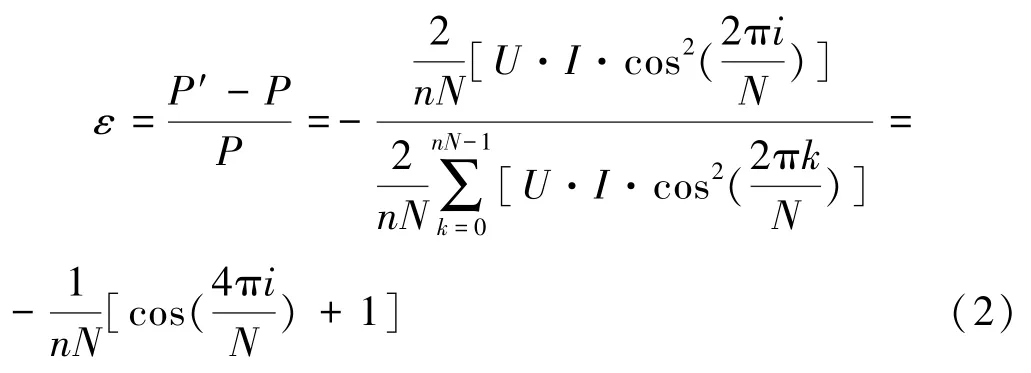
从上式可以看出,采样值报文丢失造成的误差为负误差,且误差大小与丢失的采样值报文序号有关,误差最大值为其中k即报文丢失率。数字化电能表相关国家标准中规定了采样值报文丢失测试时的丢包率为0.01%[7],此时丢失单个采样值报文数据包造成的计量误差最大值为-0.02%,误差不可忽视。
1.2 非同步采样误差
当电网频率发生波动时,FFT计算会产生频谱泄露,造成非同步采样误差[8]。非同步采样误差即非整周期采样误差,根据奈奎斯特采样定律,当采样频率是信号频率的整数倍且大于奈奎斯特频率时,在时域或者频域分析信号都有较高的精确度。若采样频率固定,当被采样信号频率发生波动时,对信号进行时域分析就会引入非同步采样误差,在频域中表现为FFT分析时出现频谱泄露,FFT算法出现电能计量误差。
电子式互感器或模拟量输入合并单元以固定的采样率对信号进行A/D采样,即当电网频率发生波动时,数字化电能表的前端设备处于非同步采样状态。若电网频率为f,取电压电流信号的初相位均为0,则有功功率可以表示为:

当电网频率发生波动,且频率偏差为Δ时,有功功率表达式变为:
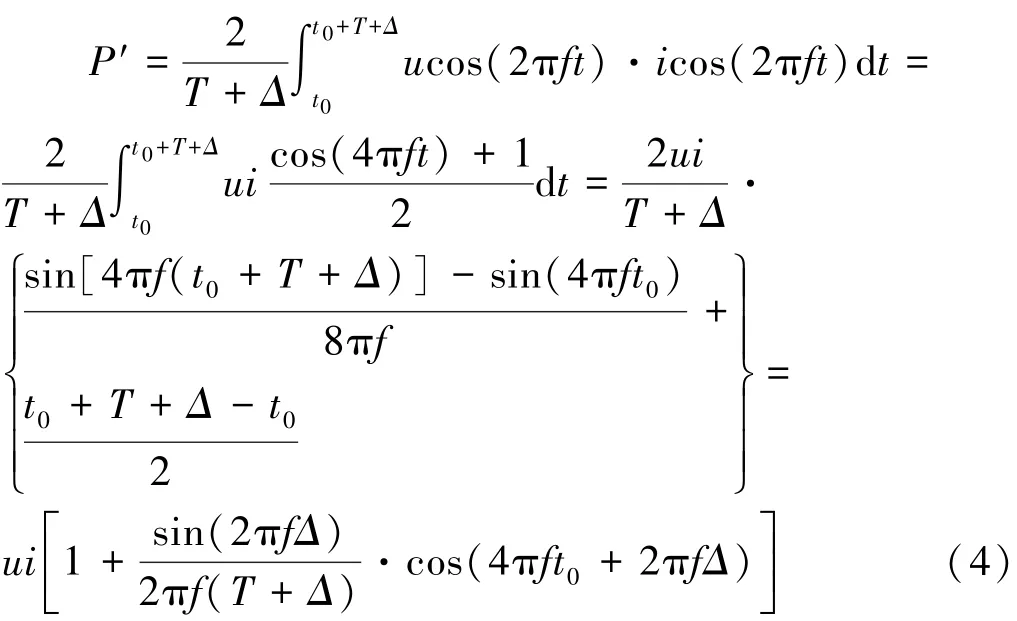
当Δ=0,即电网频率未发生波动时,sin(2πfΔ)=0,此时有功功率为P=ui。因此,当电网频率发生波动时,有功功率误差表达式为:

正常情况下,电网频率波动很小,相关国家标准规定了电网频率的偏差不能超过±0.2 Hz,当系统容量较小时,频率偏差值可以放宽至±0.5 Hz,此时有sin(2πfΔ) ≈ 2πfΔ,所以有功功率误差表达式可以变换为:

从式(6)可以看出,电网频率波动造成的有功功率最大误差为当频率波动值Δ=±0.5 Hz时,有功功率误差最大约为1%。因此,电网频率发生波动会导致传统电能算法出现较大误差。
1.3 谐波误差
电网中的非线性负载会产生谐波导致电压/电流波形发生畸变,谐波频率为基波频率的整数倍,当电网频率为50 Hz时,传统电能算法即有较好的计量性能。当电网基波频率波动为Δf时,k次谐波频率波动为k·Δf,取一个基波周期的波形进行计算,若各次电压电流的初相位均为0,与式(4)类似,得到此时的有功功率表达式:
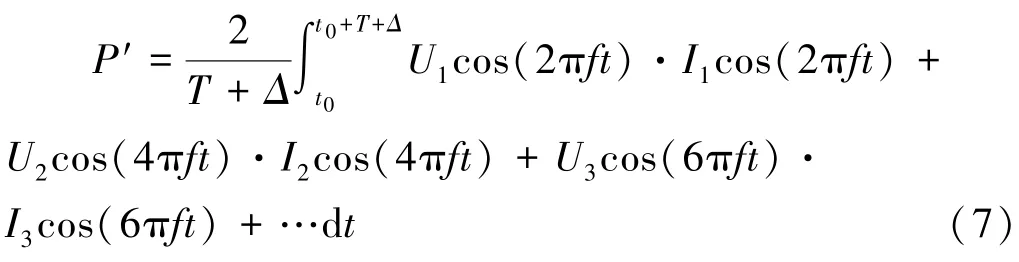
使用余弦积化和差公式,式(7)可化为:
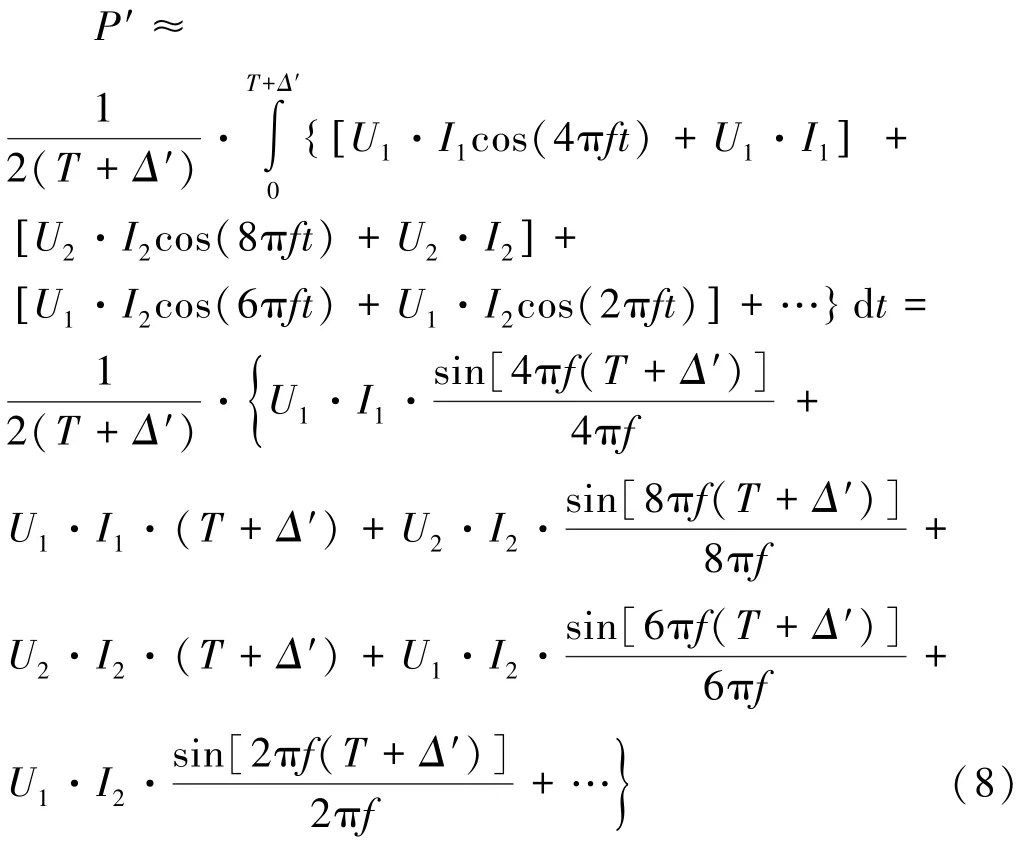
式中Δ′为频率偏差造成的基波周期变化量,其值一般很小,即有 sin(x·πfΔ′) ≈xπfΔ′,由 sin(α+β)=sinα·cosβ+cosα·sinβ,式(8)可简化为:
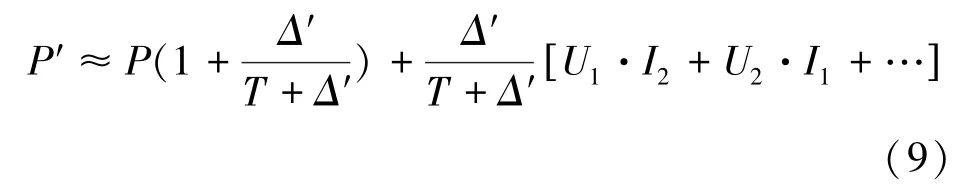
式中:

即基波频率未发生波动时的各次谐波功率。则频率波动时的谐波误差为:


与非同步采样误差类似,当基波频率波动范围为±0.5 Hz时,谐波误差约为1%,考虑误差推导过程中的舍去部分,频率偏移条件下的谐波计量误差应高于基波非同步采样误差,即谐波会使得电能计量出现较大误差。
以上分析均基于点积和算法,由分析结果可知,分析的几种非稳态工况均会使得点积和算法出现较大误差。为保证数字化电能表在现场复杂工况下的计量准确性,有必要研究具有较强现场适应性的数字电能新算法。
2 基于全相位数据处理的数字电能算法
2.1 全相位数据处理方法
传统FFT算法直接对采样数据进行截断,并对截断后的采样值序列进行周期延拓得到无限长的采样值序列。当电网频率发生波动时,周期延拓后的采样值序列在首尾相连的地方会出现跳变,即产生数据截断,FFT计算结果在频域上表现为频谱泄露。为应对数据截断产生的截断误差,将全相位数据处理方法引入数字电能算法中。全相位数据处理的主要思想可简要描述为:将一段长度为2N-1的离散数据段分为N段长度为N的数据段,并将各数据段循环移位以第N点为中心对齐,将每段数据中对应的位叠加后得到一段长度为N的数据段,最后对数据进行归一化处理得到较为连续的数据段,减弱 FFT计算时的频谱泄露现象[9-10]。
将全相位数据处理方法引入数字电能算法中。若参与数据处理的采样点数为2N-1,取N=3,分别以x n-2( )、x n-1( )、x n()为截断起始点,则截断向量为:
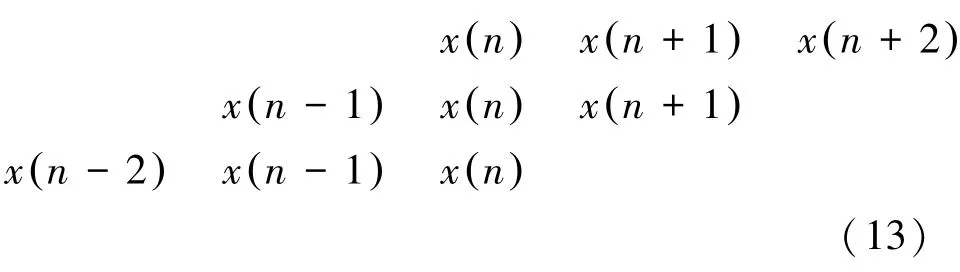
将各段数据循环移位对齐并使用矩形窗进行截断,对各段离散点进行竖直方向求和,得到全相位处理后的长度为N的全相位数据,如图1所示。

图1 全相位数据处理流程图Fig.1 All-phase data processing flowchart
全相位数据处理也可用图2中框图等价表示。

图2 全相位数据处理框图Fig.2 All-phase data processing block diagram
从图2可以看出,全相位数据处理等同于用卷积窗ωc对以x n()为中心且长为2N-1的数据向量进行加权处理,ωc为各个序列的加权窗序列f与矩形窗RN的乘积,由于上述各分段序列的加权值均为1,可得此处的卷积窗ωc为:
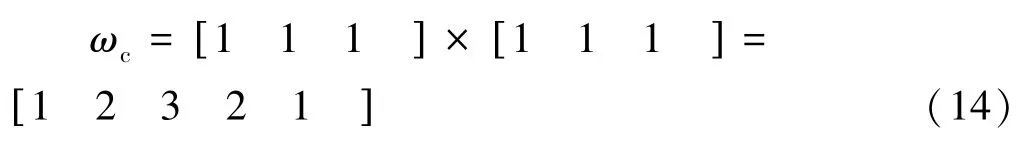
其实质为由2N-1个离散点的各个子段的加权系数向量f与后窗函数b的卷积,若f和b均为对称窗,则ωc也为对称窗,ωc的计算公式为:

为了使输入的离散点序列与输出的序列之间幅值不出现偏差,在对数据进行处理是也需要对输出序列的加权系数ωc进行归一化,归一化时选取ωc的中心点ωc(0)为归一化因子M。

2.2 电能计算方法
提出的基于全相位数据处理的数字电能算法是一种改进的全相位数据处理方法,该算法能够跟随电网频率波动自适应调节用于数据处理的采样点数。现有的全相位数据处理方法应对信号波动的能力有限,在信号频率波动较大时经过全相位数据处理后的波形连续性较差,在后续傅里叶分析时需进行加窗处理。提出的电能算法将全相位数据处理方法与插值算法结合,具有频率波动自适应能力,无需加窗处理,算法更简单,更容易在数字电能表中实现。
该电能算法首先准确计算出当前电网频率,确定用于全相位数据处理的采样点数,然后对采样值数据段进行全相位数据处理,最终采用DFT计算出基波和各次谐波的幅值和相位,从而得到相应电能量。
为了准确计算出当前电网频率,需要得到电网波形中相邻两个过零点之间的时间。在数字电能计量系统中,AD采样模块以固定采样频率Fs对电网波形进行采样,当电网频率在50 Hz周围波动时,电网波形的过零点会处于两个采样点之间,如图3所示。
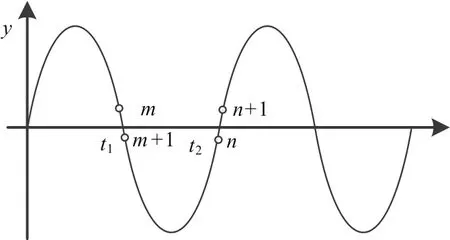
图3 采样点示意图Fig.3 Sampling point schematic diagram
采用插值算法计算过零点对应的时间t1、t2。本文以线性插值为例,计算过零点的时间。设采样点m和m+1的电压值分别为u0、u1,线性插值多项式为:
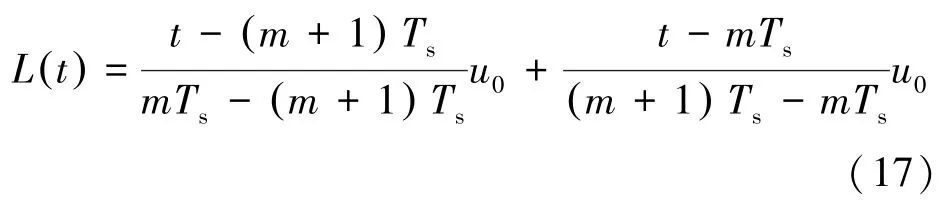
电网波形在过零点处斜率最大,即t1是使得L t()的导函数为零的点。线性插值直接将过零点两侧的点用直线相连,拟合误差较大,为提高频率计算精度,可采用高次插值算法,具体算法在此不做赘述。根据相邻两个过零点的时间差即可求出电网频率。

求得电网频率后,采用DFT算法计算经过全相位数据处理的离散值序列。根据实际电网频率计算送入DFT运算的采样点数。

式中round为就近取整运算符。DFT输出结果的频率分辨率为[11]:

即DFT输出结果序列中某一点k对应的频率为:


图4 算法流程图Fig.4 Algorithm flow chart
3 仿真试验分析
3.1 波形截断应对能力验证
以最常见的正弦波形信号为例,对自适应全相位处理前后的波形信号的连续性进行分析,数字化电能计量系统以固定的4 kHz进行数据采样,即正弦信号的频率为50 Hz时,连续80个采样点正好为一个信号周期,采样间隔为Δω=2π/80( )rad/s,若有五个单频的正弦信号,频率依次为40 Hz、45 Hz、50 Hz、55 Hz、60 Hz,则自适应全相位数据处理前后截断波形如图5所示。
从图5中可以看出,若以传统的数据波形截断方法截取数据片段,每次截取固定点数的数据,当以50 Hz的基波频率,单个周波采样80个数据点为参考标准时,80个数据点恰好为频率为50 Hz的信号的一个整周期,对于频率为40 Hz、45 Hz的信号,80个数据点不足一个信号周期、对于频率为55 Hz、60 Hz的信号,每个整周期信号采样点数小于80,即在此条件下FFT算法对此截断信号进行周期延拓后,频率为40 Hz、45 Hz、55 Hz、60 Hz的采样值序列都会出现因数据波形截断导致的不连续的现象,最终的计算结果将会出现频谱泄露。
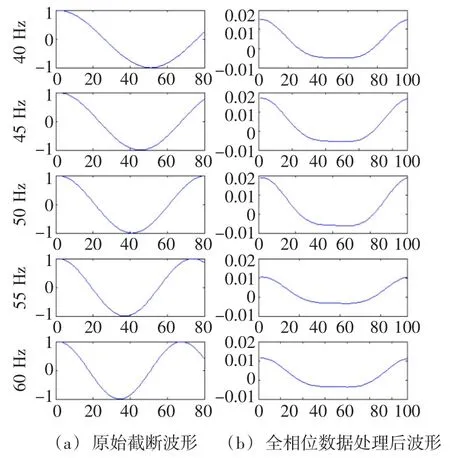
图5 波形截断仿真结果Fig.5 Simulation result of all-phase data processing
若以本文提出的具有频率波动自适应能力的全相位数据处理方法来进行数据处理,在40 Hz、45 Hz、50 Hz、55 Hz、60 Hz处得到的数据点数是自适应变动的,分别为 100、89、80、73、67 个数据点,数据处理后的波形也变为近似连续波形,解决了波形截断导致的数据不连续问题。
3.2 电能算法误差试验
根据全相位数据处理的数字电能算法研制了0.01级数字化电能表,该表一次额定电压为110 kV,一次额定电流为600 A,二次额定电压为100 V,二次额定电流为5 A。在实验室对该表和国内三个主流厂家的0.2S级数字化电能表的计量准确性进行了验证。由于在理想的基波及谐波条件下,算法的误差几乎为零,在此不再进行分析,以影响数字化电能表数值积分算法较明显的各个因素为例进行分析。各试验均取10次连续试验结果进行展示,所有试验结果图中4#电能表为研制的0.01级数字化电能表,1#、2#、3#电能表为其余厂家的数字化电能表,以数字功率源的设定值作为标准电能。试验结构如图6所示。

图6 试验结构图Fig.6 Test structure diagram
3.2.1 采样值报文丢失试验
试验电压、电流、频率均为额定值,功率因数为1.0,采样值报文随机丢失,报文丢失概率为1%。由于基本所有数字化电能表均会采用插值算法应对采样值报文丢失,所有本试验设置的报文丢失概率远高于国家标准,试验结果如图7所示。

图7 采样值报文丢失试验结果Fig.7 Sampling value missing test result
由图7可以看出,由于采用了插值算法,所有被测电能表的采样值报文丢失误差均为正值,研制的数字化电能表采用三次插值算法,其试验误差远低于其余被试电能表,误差不仅远小于0.01级电能表误差极限,且显著低于其余被测表。
3.2.2 非同步采样试验
按照最新数字化电能表技术规范T/CEC 116-2016《数字化电能表技术规范》中频率影响量试验的要求,试验电压、电流均为额定值,功率因数为1.0,频率改变为基波频率的±2%[12]。
当电网频率发生波动时,由频率偏差造成的有功功率最大误差为由图8可以看出,当试验波形频率波动-2%时,各数字化电能表误差均为正值,频率波动+2%时,误差均为负值,符合非同步采样理论计算误差。且提出的数字电能算法在电网频率波动±1 Hz时的计量误差仍显著小于其余被测电能表,具有更强的频率波动适应能力。
3.2.3 谐波负荷试验
同样按照T/CEC 116-2016《数字化电能表技术规范》中谐波影响量试验的要求,基波电压、电流均为额定值,功率因数为 1.0,5 次谐波电压U5=10%U1,5 次谐波电流I5=40I1[12],且设定基波频率波动±2%。 试验结果如图9所示。
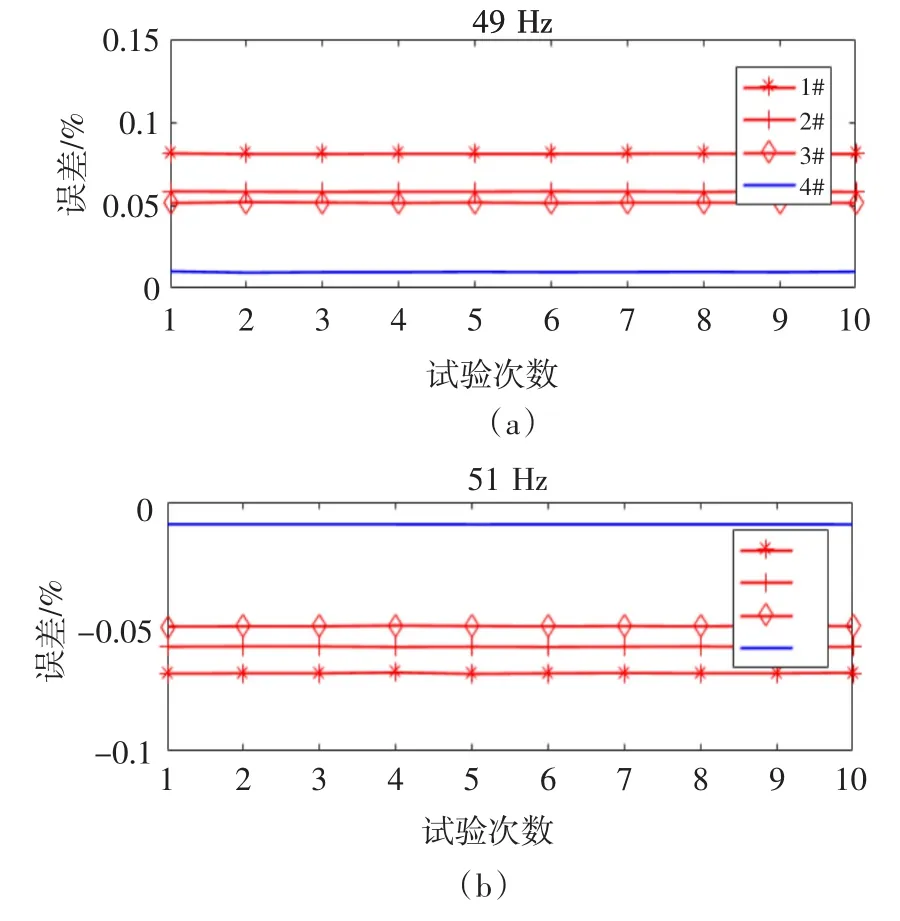
图8 非同步采样试验结果Fig.8 Asynchronous sampling test result

图9 谐波负荷试验结果Fig.9 Harmonic load test result
由图9可以看出,各数字化电能表谐波负荷试验误差分布规律与非同步采样试验基本相同,各组试验结果均略大于非同步试验,且本文研制的数字化电能表误差水平明显小于其余厂家的电能表,计量准确性更高。
从试验结果可以看出,各表均采取了一定措施以应对电网工况波动,且由于各数字化电能表均取多个周期的采样值报文计算电能,且因此实测误差均小于单周期理论分析误差。由于数字功率源的输出自带一定的误差,且采样值报文丢失具有随机性,所以各次试验结果并不完全一致。
此外,试验结果表明,与主流厂家的同类产品相比,研制的数字化电能表适应复杂工况的能力更强,在本文进行的试验中计量精度更高。
4 结束语
提出了基于全相位数据处理方法数字电能计量算法。仿真结果表明,全相位数据处理方法能有效的抑制DFT算法的频谱泄露。根据基于全相位数据处理的数字电能算法研制了标准数字化电能表,通过与国内主流厂家的数字化电能表对比试验,证明了本文提出的新算法具有较强的现场适应能力,能够在复杂负荷条件下准确计量电能。
