基于自适应陷波器的电网频率估计方法∗

王雅丽，虞莉娟，张华军，张清勇，苏义鑫

（武汉理工大学 自动化学院，武汉430070）

0 引 言

频率估计是数字信号处理的重要内容，在通信、振动控制、地震监测等方面有广泛的应用［1-2］。在现代电力电子设备中，由于电网频率和相位信息是功率开关管（IGBT、IGCT、GTO）开通和关断的参考，一旦开通或关断不准确可能导致设备中出现环流，环流过大则会影响多台设备之间的并联效果，严重时甚至会烧毁功率开关管［3-4］，因此电网电压信号的实时在线频率估计是十分必要的。由于自适应陷波器结构简单，具有尖锐的阻带截止特性，且能够根据外部环境的变化自动调节陷波参数，因此被认为是一种良好的频率估计滤波器［5］。常用的频率估计方法主要有傅里叶变换法［6-8］、最小误差平方法［9］、小波变换［10］、最小二乘法［11］等，此类方法计算量较大，对算法实现的硬件载体要求较高。因此，针对频率动态变化的信号，可采用自适应陷波器以获得准确的频率信息［12］。同时为了估计信号中多个频率信息，通常将多个单频陷波系统级联实现多频率估计［13］，但该方法的结构和陷波器参数调整算法均较复杂，不易于工程实际中的应用。

本文针对电力系统频率估计问题，提出一种二阶自适应陷波器频率估计方法，结合电网电压信号基波和谐波的特性，以陷波器实时输出平方值为陷波器参数优化目标函数，根据随机优化理论推导了陷波器参数在线迭代算法。通过仿真研究和实验测试，检验了所提出的频率估计算法的响应速度和估计误差。

1 二阶陷波器原理

陷波器也叫带阻滤波器，能保证在其它频率成分不失真情况下，有效地滤除输入信号中特定的频率成分［14-17］。对于二阶陷波器，应满足其传递函数的零点在单位圆上，以使陷波深度无穷大，同时传递函数的零点与极点应匹配，以使除陷波频率ω0外的其他频率成分不受影响。因此，可在单位圆上角度为ω0处引入一对复共轭零点z1，2=e±jω0，且在零点径向附近放置一对复共轭极点p1，2=re±jω0（ 0＜r＜1），以减小陷波带宽，则二阶陷波器的零极点位置配置原理如图1所示。

图1 零点和极点的位置Fig．1 Position of zeros and poles

可得二阶陷波器传递函数：

又由于：

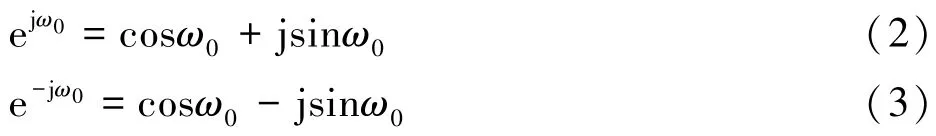
因此，二阶陷波器传递函数可化为：

二阶陷波器结构原理如图2所示。

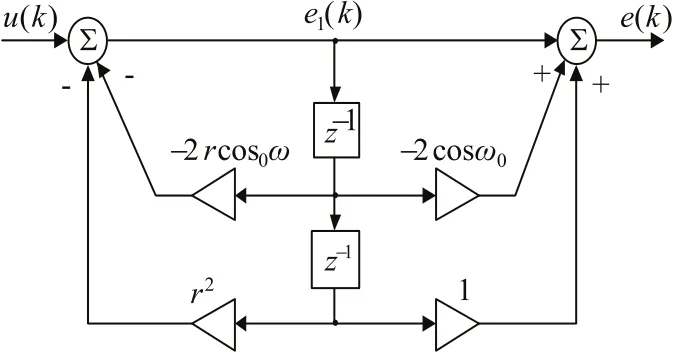
图2 二阶陷波器原理Fig．2 Principle of second-order notch filter

其中u（k）表示陷波器输入信号，陷波器各级输出信号分别用e1（k） 、e（k） 表示。

令a=-2cosw0，代入式（4）可得：

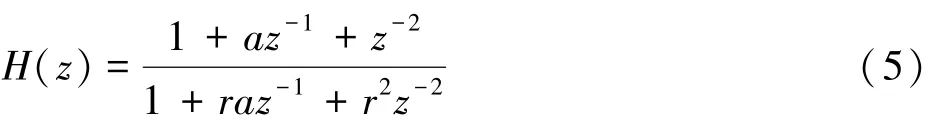
其中r称为极半径参数，且0＜r＜1，即极点在单位圆内，系统稳定。二阶陷波器的幅值特性如图3所示，由于零点在单位圆上，所以传递函数在ω=ω0处的凹口深度为无穷深，几乎可以完全滤除特定的频率成分。

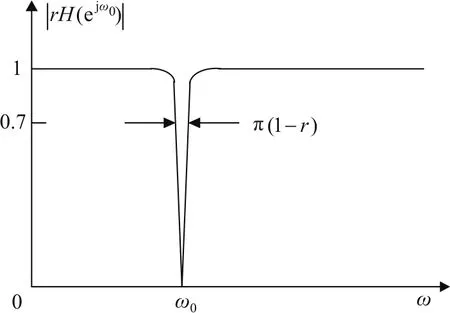
图3 二阶陷波器幅值特性Fig．3 Amplitude characteristics of second-order notch filter

此外，凹口的尖锐程度是由传递函数极点和零点的接近程度 1-r大小决定，即凹口带宽BW=π (1-r) ，可由品质因数Q=f0／BW=2／ω0（1-r） 来表征。对于特定的频率成分，极半径参数r越大，则极点越靠近单位圆，频率响应曲线凹陷越深，陷波器凹口带宽越小，品质因数越大，陷波效果越好；反之，极半径参数r越小，则极点离单位圆越远，频率响应曲线凹陷越浅，陷波器凹口带宽变窄，品质因数越小，陷波效果也越差。当r=1时，陷波器成为只滤除频率ω0的理想滤波器。图4描绘了陷波频率ω0=50 Hz时不同的极点半径r造成的滤波器幅频特性曲线。

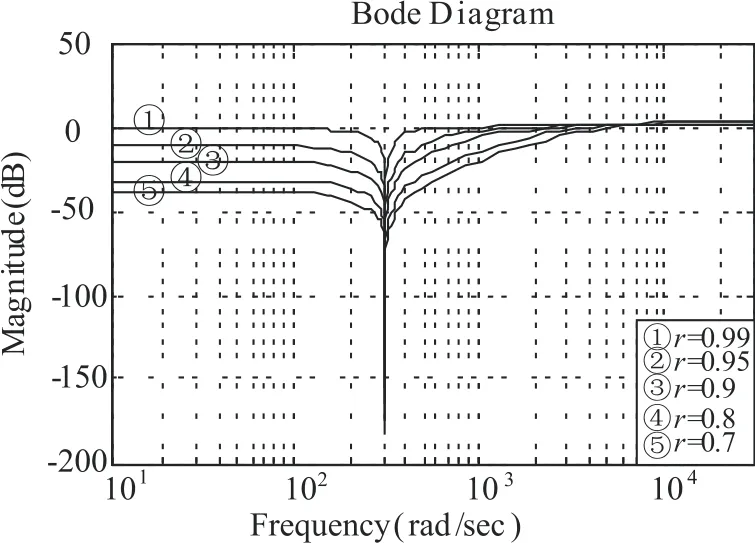
图4 不同r对应的陷波器幅频特性曲线Fig．4 Amplitude-frequency characteristic curve of the notch filter corresponding to r

从图4中还可以发现，陷波器的带阻频率与归一化频率w0之间不同，这种原因在于归一化频率需要根据不同的采样频率来计算实际的带阻频率。陷波器带阻角频率ωstop=ω0×fs，带阻频率fstop=ωstop／2π 。 此外，r越大，则对陷波频率以外的其他信号的衰减越小，在实际应用中可以根据实际的滤波效果选择合适的r。

通过以上分析可知，a为与陷波频率ω0有关的陷波器参数，因此可通过调节参数a对信号频率进行估计，即选取适当的极半径r，固定陷波带宽，通过自适应调整陷波参数a，将谐波信号几乎完全滤除，对基波信号频率实现实时在线估计。

2 交流电压自适应频率估计

在电力系统中［18-19］，由于受到非线性负载的影响，稳态的工频供电电压波形将偏离正弦波形而发生畸变，以若干个正弦波叠加的形式可将电网电压信号表示为：

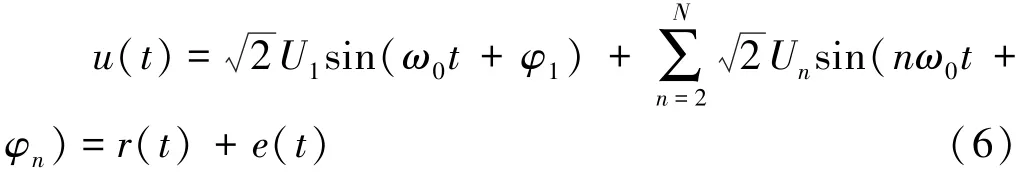
式中r（t）表示在电网电压信号中占主要成分的基波信号；e（t）表示其他一些能量较小的信号，即谐波信号；且U1、φ1分别为基波电压有效值和初相位，Un、φn分别为第n次谐波电压有效值及初相位。

在用自适应陷波器对电网电压基波信号的频率进行估计时，其原理如图5所示，可将含有n次谐波的电压信号作为陷波器输入信号，通过自适应算法对基波频率的梯度搜索及陷波器的滤波作用，可达到基波信号r（k）与谐波信号e（k）分离的目的，进而对信号频率进行估计。由于在最小均方误差准则下，一旦陷波器没有完全滤除基波信号，则陷波器输出的谐波信号能量便会增加，对基波信号的频率估计将不准确，因此应适当选取陷波器的有关参数，尽可能将谐波信号完全滤除，提高频率估计的准确性。

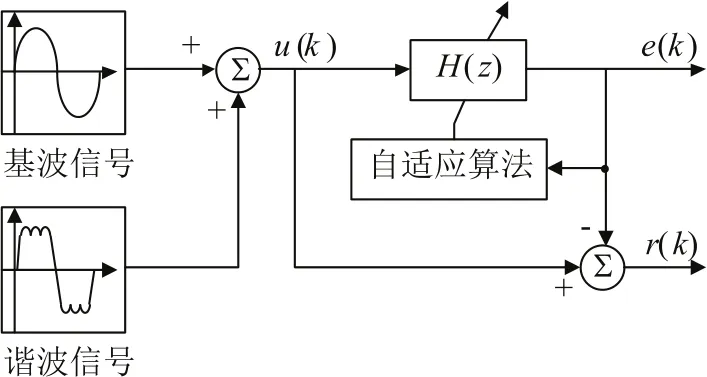
图5 自适应陷波器原理Fig．5 Principle ofadaptive notch filter

建立如下参数优化目标函数：

式中e（k）是输入信号u k()经过陷波器H z()后输出的误差信号，则目标函数梯度为：

又由陷波器传递函数可得：

则 de k()／da为：

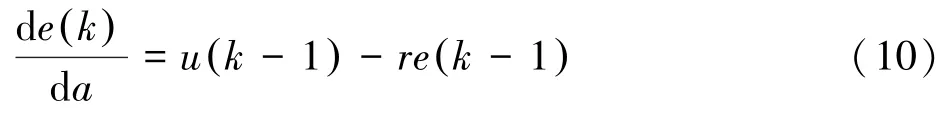
因此目标函数梯度g k()为：

根据梯度搜索迭代公式，参数a的迭代公式为：

若令α=2μ，则：

式中α为迭代步长，也称学习速率，且α＞0，影响系统的控制精度和响应速度。α越小，即学习速率越慢，输出信号失调越小，但响应速度变慢；反之，α越大，即学习速率越快，会导致较快的响应速度，但输出信号的失调也变大，可能导致算法无法收敛［20］。在工程应用中需根据实际情况折中考虑，做出最佳选择。

3 仿真研究

为了对所提出的频率估计方法展开更进一步的分析、验证，首先在基波频率固定的情况下对电压信号进行跟踪实验研究。以电网单相电压信号频率估计为例，取采样频率fs=10 000 Hz，极半径参数r=0．99。将待估计频率ω0=50 Hz的基波信号注入3次，5次和7次谐波，其幅值分别为基波幅值20%，13%和11%的信号作为输入信号，如图6所示。即采样得到的电压信号为：

图6 输入信号u t()曲线Fig．6 Curve of the input signal u t()

表1为取待估计频率f0=50 Hz，当初始带阻频率从f=50．1 z至f=60 z变化，步长α分别为 0．5×10-10、 1．0×1010、 1．3×10-10、 1．5×10-10、 2．0×10-10时，针对提出的频率估计方法从响应时间与估计误差两方面进行对比的结果。从表中可以看出，当初始带阻频率相同时，随迭代步长的增大，自适应陷波系统的超调量逐渐增大，陷波参数曲线的响应速度越来越快，但频率估计精度将随之小幅降低。当步长相同时，陷波参数曲线的估计误差与初始带阻频率无关，表明该方法具有较好的频率估计稳定性能，但当初始频率f与待估计频率f0非常接近时，由于初始梯度较大，会引起陷波参数曲线较大的振荡，响应时间增大；若初始频率f与待估计频率f0相差较大，则亦会增大梯度搜索时间，即响应时间增长。综上，应选择合适的初始频率同时满足较小的响应时间和较小的估计误差。

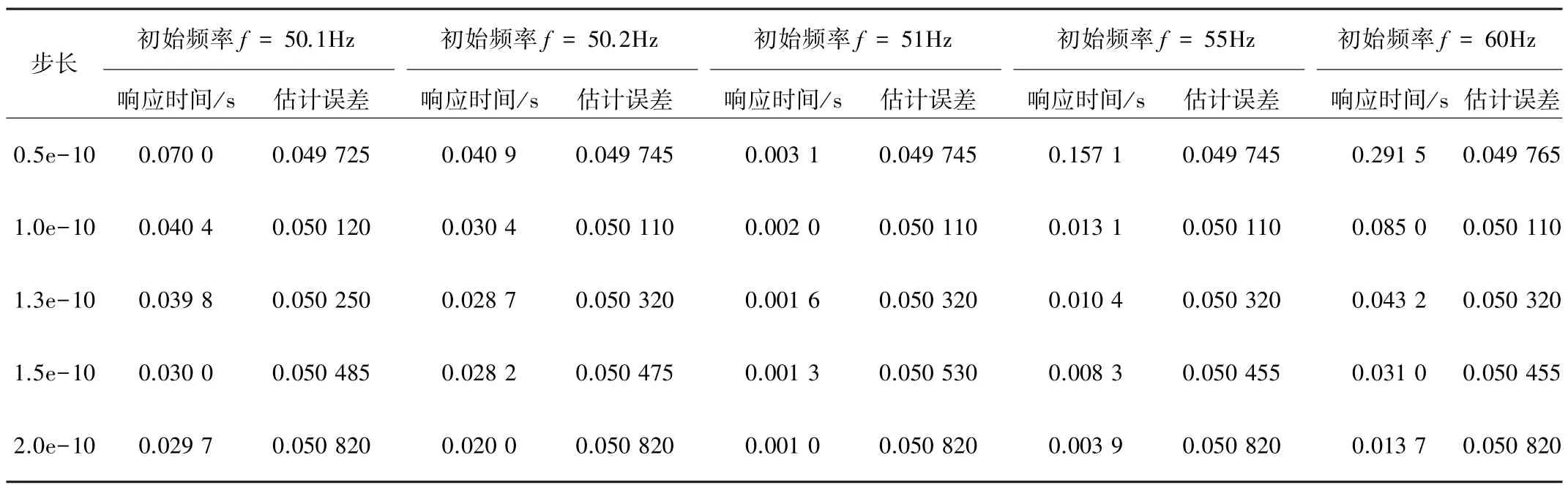
表1 初始频率f和步长均不同条件下陷波参数曲线响应时间与估计误差对比Tab．1Comparison of the response time and the estimation error of notch parameter curve under different conditions of initial frequency and step length

根据表1分析，且为适应更宽范围的频率波动，仿真测试中陷波器的初始带阻频率设置为60 Hz，即参数的初始值为：a=-2cos( 2π×60／10 000)。

由以上分析可知步长α对自适应陷波器的频率估计性能有重要影响，通过式（13）的迭代计算，可得图7所示在不同步长情况下参数a收敛曲线。综合比较系统可知，当步长α=1．3×10-10时，陷波参数a经过约800次算法迭代收敛于最优值，即收敛时间ts=0．08 s，相较于其他步长收敛速度更快，且控制精度较高。由此验证了式（13）所示算法具有全局收敛能力，可以应用于工程实际。

取步长α=1．3×10-10，可得图8所示陷波器输出误差信号曲线，电压基波信号经过陷波器带阻频率逐步调整后，误差信号随之逐渐减小，当陷波参数a收敛于理论最优值时，输出误差信号也趋于稳定，为3次、5次和7次谐波信号叠加。将输入信号与陷波器输出误差信号线性叠加，即可准确提取图9所示待估计频率的电压基波信号，进而获得基波信号频率，从而验证了式（13）中提出的自适应迭代算法的有效性。

图7 参数a收敛曲线Fig．7 Convergence curve of the parameter a

图8 输出信号e t()曲线Fig．8 Curve of the output signal e t()

图9 自适应陷波系统输出的电压基波信号Fig．9 Fundamental waveform signal output by the adaptive notch system

4 实验验证

为进一步验证所提频率估计方法的有效性及工程应用的可靠性，将此方法应用于对实际电网电压基波信号的频率估计。实验利用图10所示的LV25-P／SP5电压互感器对输电线路上单相电压信号进行采集，采样频率fs=10 000 Hz，得到的电压信号曲线如图11所示，可以看出采集的相电压含有很小的谐波畸变信号。另取极半径参数r=0．99，陷波器的初始带阻频率为60 Hz。

图10 电压互感器Fig．10 Voltage transformer

图11 输入信号u t()曲线Fig．11 Curve of the input signal u（t）

将采集到的电网电压信号输入自适应陷波系统，经过自适应算法调整，得到图12所示的参数a收敛曲线及图13所示的陷波器输出误差信号曲线，最终系统将输出稳定的电压基波信号曲线，即谐波干扰信号被完全滤除，准确提取出了工频ω0=50Hz的基波信号。

图13 输出信号e t()曲线Fig．13 Curve of the output signal e t()

5 结束语

提出一种新的基于自适应陷波器的简单频率估计方法，运用随机优化的方法对自适应陷波器的参数进行配置，使陷波器检测得到的基波信号频率不断逼近待估计信号频率，实现基波信号的准确提取。将此方法应用于频率恒定信号的跟踪，对含谐波的电网电压基波信号进行频率估计，响应速度较快，稳定性较高。通过Simulink仿真分析及实验平台的验证，进一步说明了此方法的收敛性、有效性以及实时性，可应用于工程实际。