海洋双桩基础周围流场特征数值模拟

， ，

(1. 浙江同济科技职业学院 建筑工程系， 浙江 杭州 312231； 2. 中交四航工程研究院有限公司，广东 广州 510230； 3. 浙江大学 建筑工程学院， 浙江 杭州 310058)

0 引 言

海上构筑物(海上风机、海洋平台等)采用多桩基础，其桩群周围的流场十分复杂，可能导致床面泥沙产生显著的局部冲刷，影响海洋结构物的稳定与安全。研究表明，基础周围冲刷的本质是桩周流场的改变，导致局部床面切应力增强，进而产生冲刷。ATAIE-ASHTIANI等[1]对在恒定流作用下不同桩数、不同桩排布时的清水冲刷情况进行物理试验研究。MOSTAFA等[2]通过物理模型试验研究在波流作用下的群桩周围冲刷，探究桩数、桩位变化对桩周局部冲刷的影响。LIANG等[3]则对双桩的桩间距以及迎流方向对桩周冲刷深度的影响进行研究。

本文构建双桩基础周围的三维流场数值模型，计算分析不同桩间距、入流角度对桩周流场结构的影响。研究发现：在稳定单向流作用下，双桩周围出现壅水、向下冲击水流、立轴状小漩涡等流场结构；最大床面切应力位于双桩两侧边缘，且随桩间距的增大，先增大后减小；不同迎流角度布置的双桩对床面切应力分布有较大影响，并排布置的双桩其最大床面切应力最大，位于桩的两侧边缘，而45°交错布置的双桩，最大床面切应力在双桩的内侧边缘。

1 计算流体力学数值模型

1.1 流体方程

本文的三维流场数值模型基于连续性方程和不可压缩黏性流体运动的Navier-Stokes方程，其具体表达式如下。

连续性方程为

(1)

动量方程为

(2)

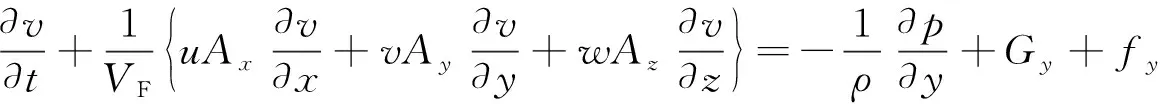
(3)

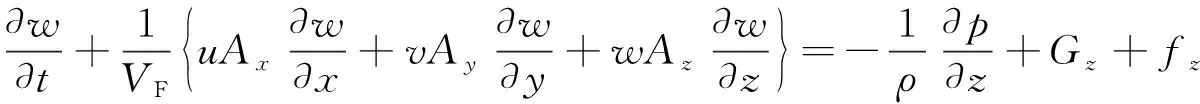
(4)

式中：u、v、w分别为物体在x、y、z等3个方向的速度分量；Ax、Ay、Az分别为x、y、z等3个方向可流动的面积分数；t为计算时间；VF为可流动的体积分数；ρ为液体密度；p为液体动量；Gx、Gy、Gz为x、y、z等3个方向的重力加速度；fx、fy、fz为x、y、z等3个方向的黏滞力加速度。在模拟湍流方面，采用RNGk-ε模型，考虑平均流动中的旋转及旋流流动情况，可以处理高应变率及流线弯曲程度较大的流动。

1.2 模型设定

将整个数值计算域分为流场发展段和模型试验段等2部分进行建模，其中：发展段模型长15.5 m，宽1.0 m，高0.7 m，用以保证流场的充分发展稳定；试验段模型长4.5 m，宽1.0 m，高0.7 m，用于模拟桩周的流场结构。以入流截面底边角点为原点，建立空间直角坐标系，取水流流动方向为x轴正方向，竖直向上为z轴正方向。在数值模型中，取桩径D=0.1 m，双桩底面圆心连线与x轴垂直且位于x=17 m位置处。如图1所示，本文设置了一系列双桩间距G分别为0.5D、1D、2D、3D梯度的数值模型以研究不同间距双桩周围的流场特性。此外，在双桩间距G为2D情况下设置双桩中心连线与水槽中心线成0°(串联)、45°(交错)、90°(并联)等3种情况的数值模拟，以研究在不同迎流角度下双桩周围的流场特性影响。

试验段模型在x、y、z方向的网格单元数分别为180×50×75，单元形状为均匀六面体。为准确模拟双桩周围流场变化，在双桩周围设置网格加密区域，计算域截面的网格分布如图2所示。其中，x方向1.2 ～2.2 m范围内网格大小设为8.33 mm。如图2 a)所示，y方向0.1～0.9 m范围内网格大小设为6.67 mm。如图2 b)所示，z方向0 ～0.1 m范围内网格大小设为4 mm，而0.1 ～0.3 m范围内网格大小设为10 mm。

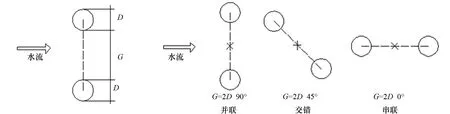
图1 计算工况示例

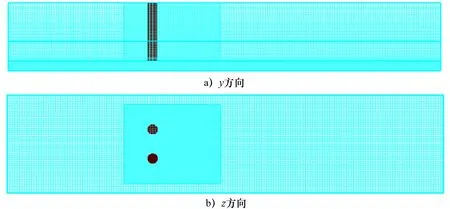
图2 数值模型网格剖分

1.3 边界选择及初始条件

对于发展段模型，入口边界使用入射流速边界，出口边界使用连续边界，求解得变量的法向导数都为零，使流体在出流边界处呈现自由流出形态。前后边界及上边界均采用对称边界。下边界被设置为壁面无滑移边界。试验段模型的入口边界同样为速度边界，在计算时将发展段模型的出口流速分布数据直接导入。

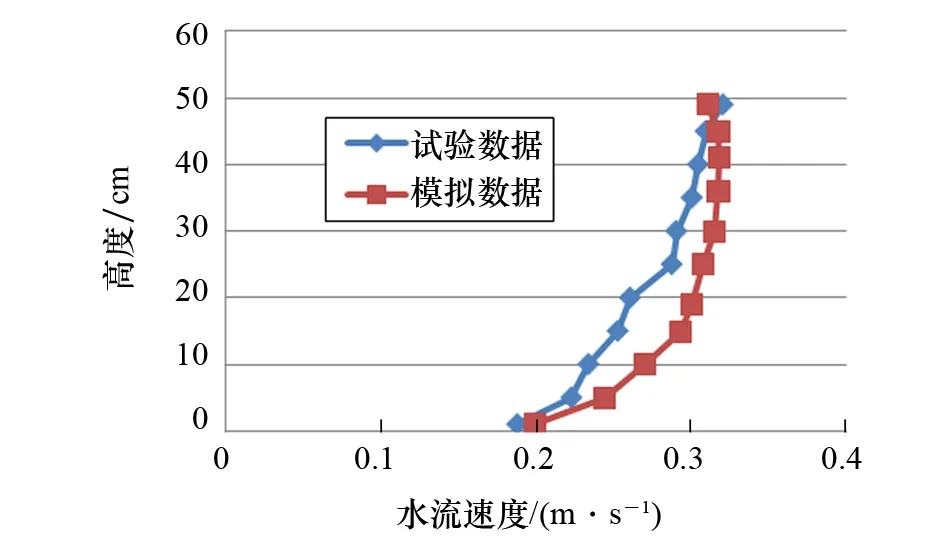
图3 数值模拟与试验结果的流速分布对比验证

设定重力加速度大小为9.8 m/s，方向沿z轴负方向。设置桩体表面的静摩擦系数为-1，表示表面无滑移。表面粗糙度设置为0.001，为砂浆混凝土材料推荐值。计算域内的流体初始流速设定为入射流速，初始流速的分布高度等于初始液面高度，初始压力分布采用静水压力。

1.4 数值模型验证

为保证试验段的数值模拟精度，首先需对发展段数值模拟所得的流场进行分析检验。模拟初始阶段，水流由水槽一端冲向另一端，经过一段时间后达到稳定状态。根据物理模型流速测点分布，本文提取了数值模型对应位置桩前1 m处的流速垂向分布，与数值模型数据相比较，以验证纯流模型所设置的湍流方程、初始条件、边界条件等的可靠性，如图3所示。从图3可以看出：数值模拟所得流速分布情况与试验结果较为吻合。

进一步与SUMNER等[4]的研究结果进行对比分析，验证所建立数值模型能否较好地描述双桩周围的三维水流运动。图 4a)为SUMNER等在双桩间距G=0.5D情况下得到的桩后流态图，而图 4b)是数值模拟所得桩后涡量图，可以看出：数值模拟与物理试验均表明当间距较小(0.5D)时，双桩间的相互影响使得两桩周围流态不对称，桩后一段距离后才发生漩涡脱落。

图4 与SUMNER等的试验结果进行流态对比

2 双桩间距2D流场特征

本文首先以双桩间距G=2D为例，计算分析双桩周围局部流场结构特征，具体计算结果如下。

2.1 发展段流速分布

当发展段模型模拟运行至80 s时，由于底边界使用壁面边界条件，流体在与壁面间的摩擦阻力作用下，形成了近底床处的水流流速最小、向上逐步发展的流速竖向分布。在x=15 m处，水槽中心线处沿z方向的流速分布曲线在选取的80 s、85 s、90 s等3个时间点上完全重合，这说明在90 s模拟后，发展段下游(15 m后)已经形成稳定的流场，可以在此区域后设置双桩，进行流场结构的研究。

2.2 桩周流场分析

由于桩体阻碍作用(见图5 、图6)，靠近桩前端水流速度会逐渐降低，水面逐渐升高并发生壅水(见图7)。在桩体后侧，由于迎水面水流的向下运动和桩基两侧的侧向绕流，使桩基后侧水面降低。而圆柱桩两侧的水流高度也随桩基前端沿的水流增高而升高，但桩两侧液面变化并不对称(见图8)。

图5 单个桩桩周流场矢量图 图6 桩前底部向下水流矢量图

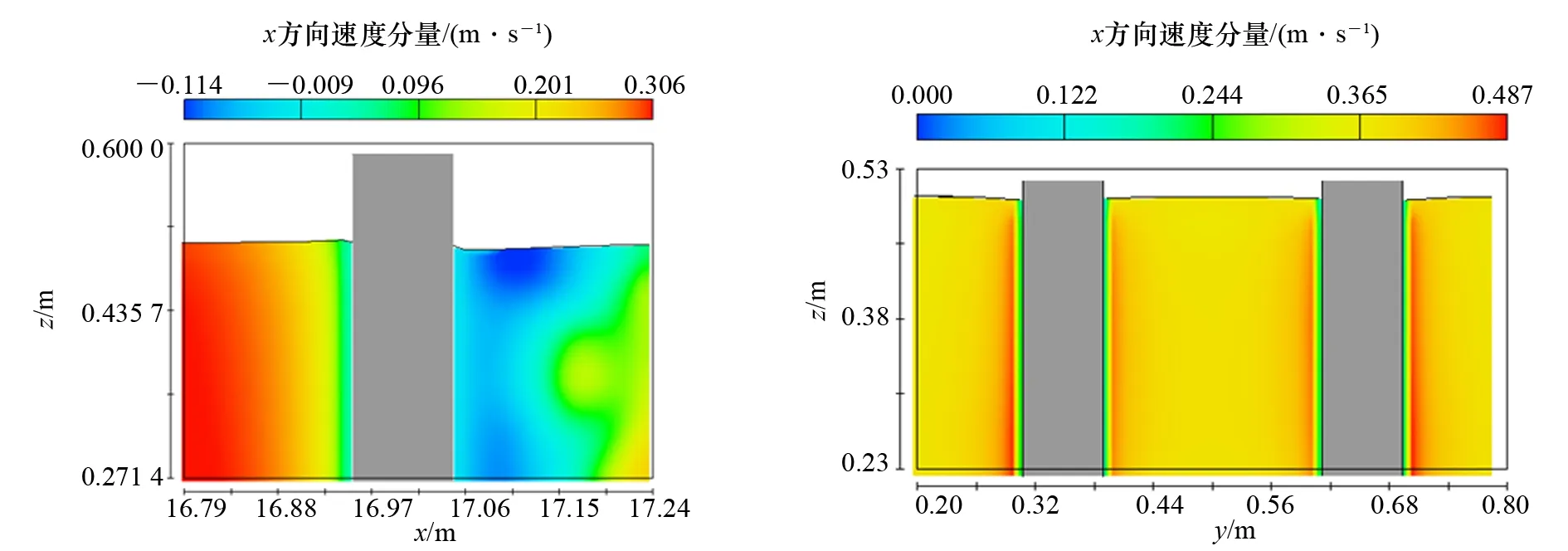
图7 沿水流方向液面高度示例 图8 桩侧液面高度示例

此外，通过分析桩周围流线变化，可以清楚观测到柱体周围的典型水流特征。如图9所示，柱体前端水流受阻后，迎水端出现自由表面壅起，靠近上部的水流流速大，靠近底层的流速小，部分水流沿桩身向下流动。在桩周近底部的边界层分离早于桩周上部。桩两侧绕流在桩基和正常水流的夹持下，在圆柱后端及左、右侧面的垂直方向上形成一个负压力梯度，产生向上水流和自近床面释放的立轴状漩涡(小漩涡)。水流通过圆柱桩后，被挤压的水流向桩后扩散，边界层分离，在桩后形成紊流(尾流漩涡)，其横向绕流更加明显，绕流宽度逐渐减小，水流方向发生变化。横向漩涡向下流动，受水槽床面的阻挡，与圆柱两侧的绕流水流相互作用在桩前形成横轴环状漩涡带(马蹄形漩涡)。桩间距中心区域的流线在方向上未发生明显变化，在双桩间变化较为对称，除了近桩侧部分的绕流扩散形成的小部分漩涡，双桩内侧中间区域的流场相较于双桩外侧更为稳定。

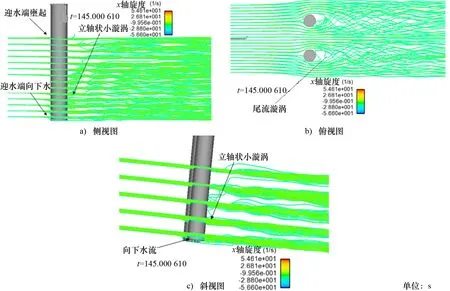
图9 并排双桩桩周流线分布

图 10为并排双桩柱体周围的三维涡量场分布，漩涡在竖直方向上会逐渐分离为2个独立单元，其脱落形态类似破碎的龙卷风。底部漩涡的脱落要落后于上部的尾涡脱落，且脱落发生的位置大致是1倍桩径水深处，底部涡流的旋转方向与上部的旋转方向相反。两个桩后的尾涡存在明显的反对称，由于底部和上部的流速差异，近床面处的尾涡范围要比上部的范围小，底部漩涡较上部漩涡小。

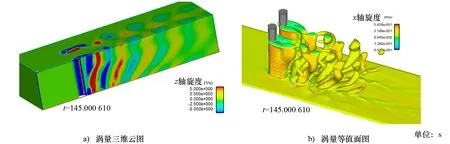
图10 并排双桩桩周三维涡量场分布

3 桩间距改变时流场特征

本文使用0.5D、1D、2D、3D等4种不同桩间距的数值模型研究桩间距改变时对桩周流场结构的影响。研究发现，桩间距G=0.5D时双桩绕流流线不对称，双桩距离近，剪切层产生相互影响，无明显的对称摆动现象。随桩间距增大，双桩影响减小，桩周流场变化较为独立，如图 11所示。随双桩间距的增加，yz断面流体的x向流速最大值也随之减小。

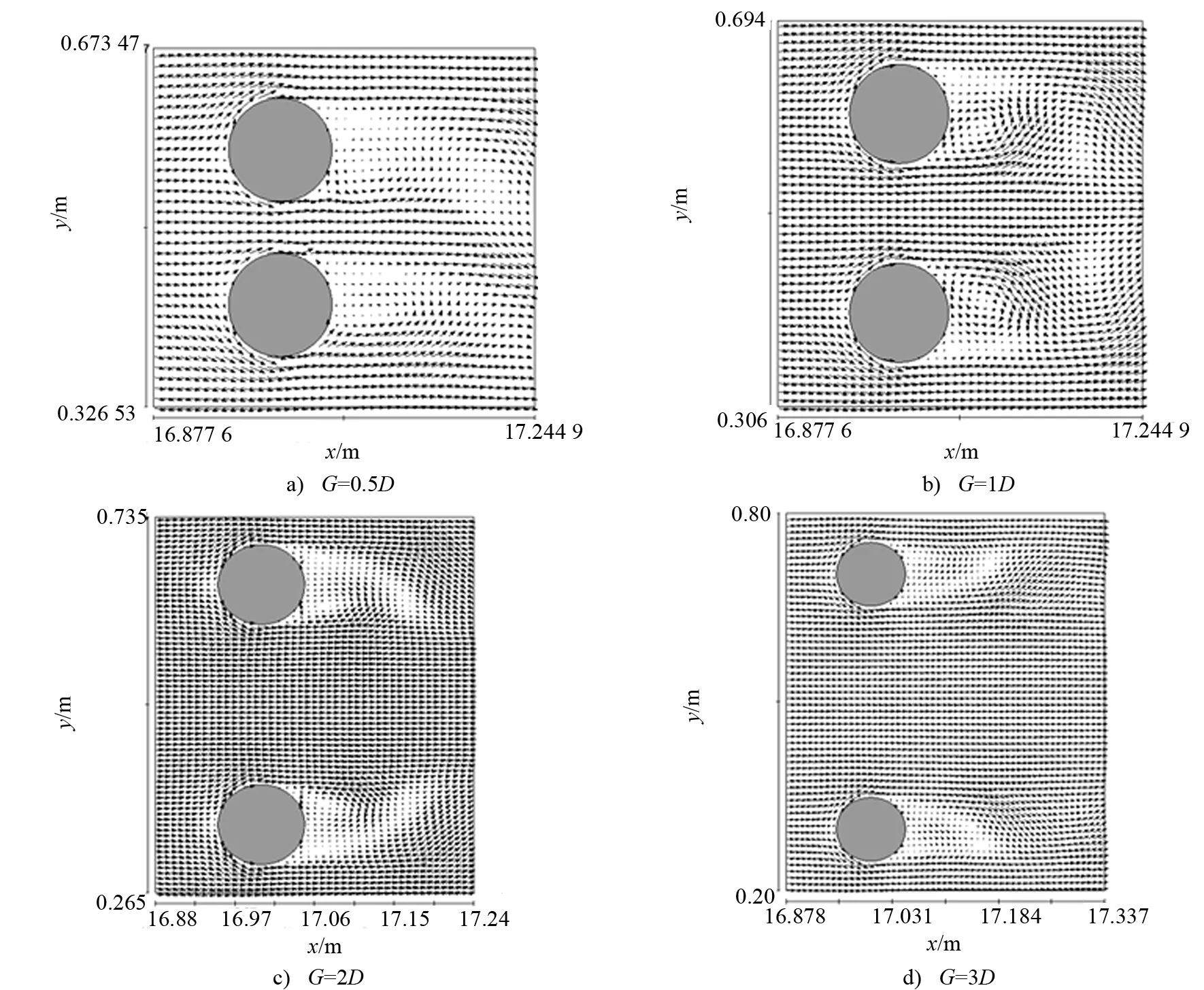
图11 t=40 s，h=0.03 m时不同桩间距时桩周流场速度矢量图

如图12所示，单个桩的桩后涡量分布随双桩间距的增大而逐渐具有反对称性。同时，间距的改变影响桩后漩涡脱落的频率，桩后漩涡发展脱落的区域也有所不同：当双桩间距G=0.5D时，涡流在内部剪切层发展，由于近壁效应，漩涡在桩后一段距离才发生扩散、脱落；当双桩间距G=3D时，单个桩的桩后涡量分布表现较为独立，表明双桩的影响作用随间距增大而减弱。

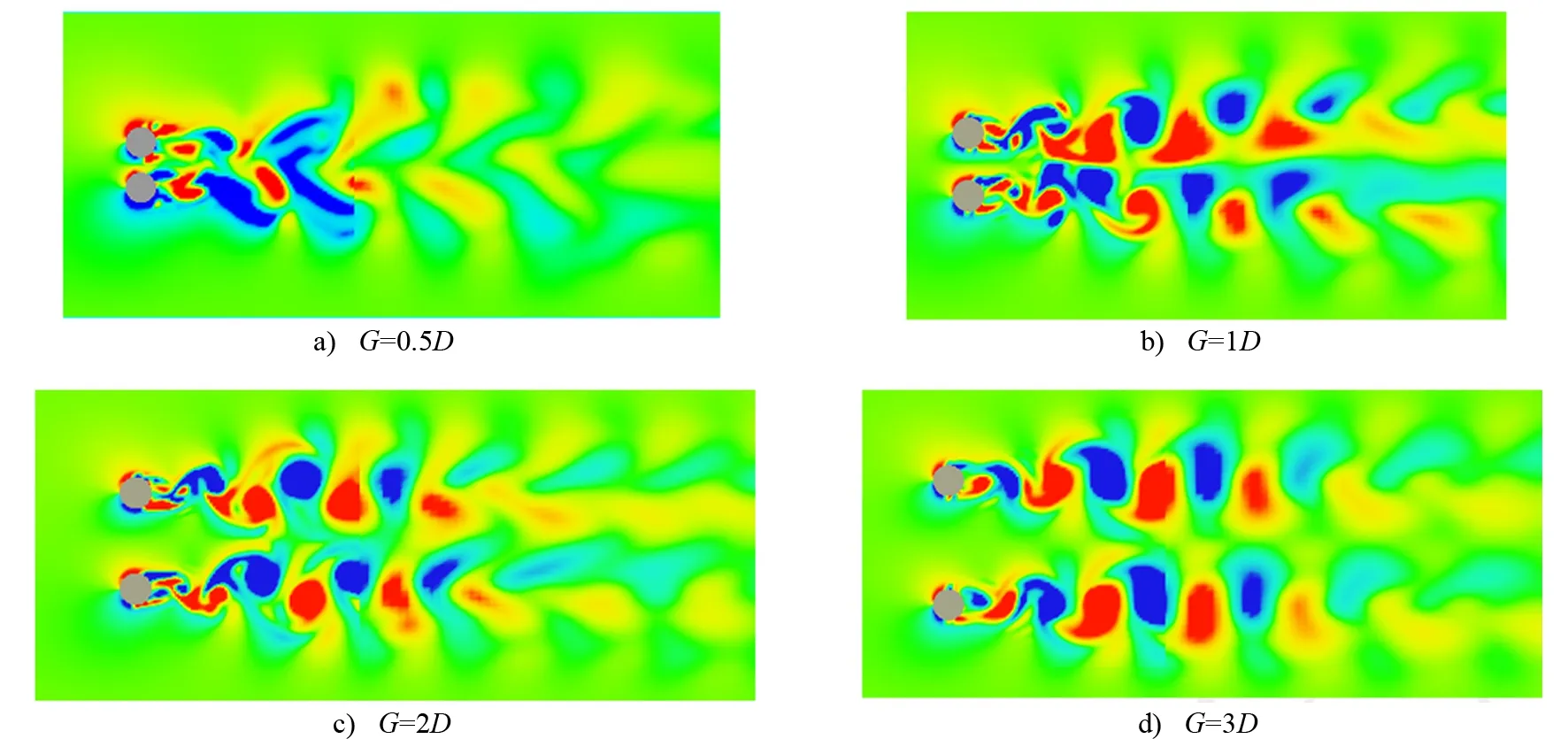
图12 t=40 s，h=0.03 m时不同桩间距模型桩后涡量分布图

4 入流角度变化时流场特征

串联布置的双桩，前桩的yz断面流速分布对称，而后桩的断面流速分布不对称，下游桩的最大断面流速比前桩大。前桩断面流速在桩侧取得最大值，而后桩在距两侧边缘一定距离处取得最大值。取得前后两桩连线中心yz断面的流速分布图，发现存在一个反方向流速区域——“回流区”，阻碍前桩的自由剪切层的发展，难以在双桩间形成漩涡脱落，且两桩中间区域的yz断面流速分布不对称，如图13所示。

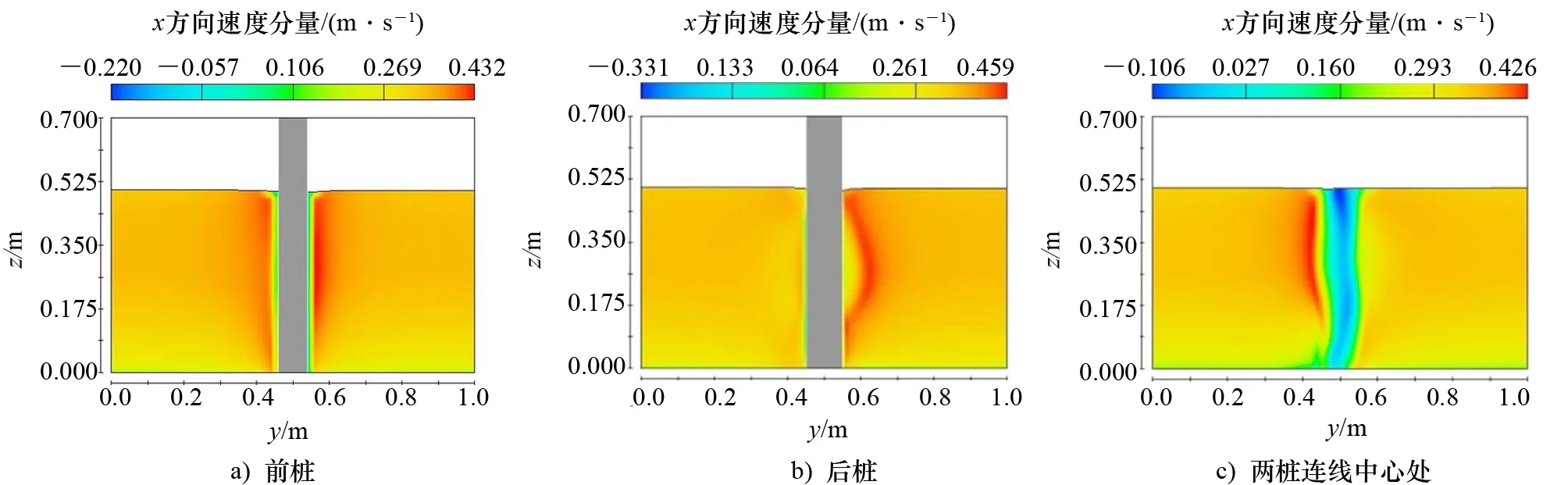
图13 串联双桩桩周yz断面流速分布

对于与流向呈45°布置的双桩而言，通过双桩中心的xz断面流速分布图(见图14)发现：前桩和后桩在桩后都存在1个反向流速区，两桩的整体流速分布情况类似；后桩桩后形成稳定的漩涡脱落，但由于后桩的存在，前桩的剪切层发展受到干扰，紊动明显，尾涡仍在发展。同时由于两桩中间区域也存在1个反向流速区域，导致前桩的两侧流速不对称，外侧的流速大，但后桩两侧的流速相对较为对称。因此，在流速分布上，前桩对后桩的影响较后桩对前桩的影响要小。

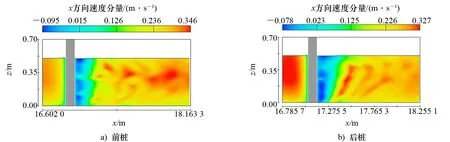
图14 与流向呈45°布置的双桩桩周流速分布

如图15所示：串联布置的双桩，前桩的剪切层发展成熟向下输送，撞击下游的圆桩，形成涡流脱落的流态，前后两桩的干扰以尾流效应为主，漩涡脱落呈现反对称；与流向呈45°布置的两桩，其存在前后和上下2种剪切层，以及还面临前桩尾流的共同作用，涡量分布非常复杂。

图15 t=30 s, h=0.47 m处不同入流角度双桩桩周涡量分布

如图16所示：前后排列的双桩下游桩的涡量图与上下排列的双桩涡量图相似，漩涡在竖直方向上脱落分为2个单元，底部漩涡脱落要落后于上部漩涡脱落；前后双桩涡量的底部干扰较上部更为明显；与流向成45°布置的双桩，距离桩后较长一段距离后尾涡发生上下分离。

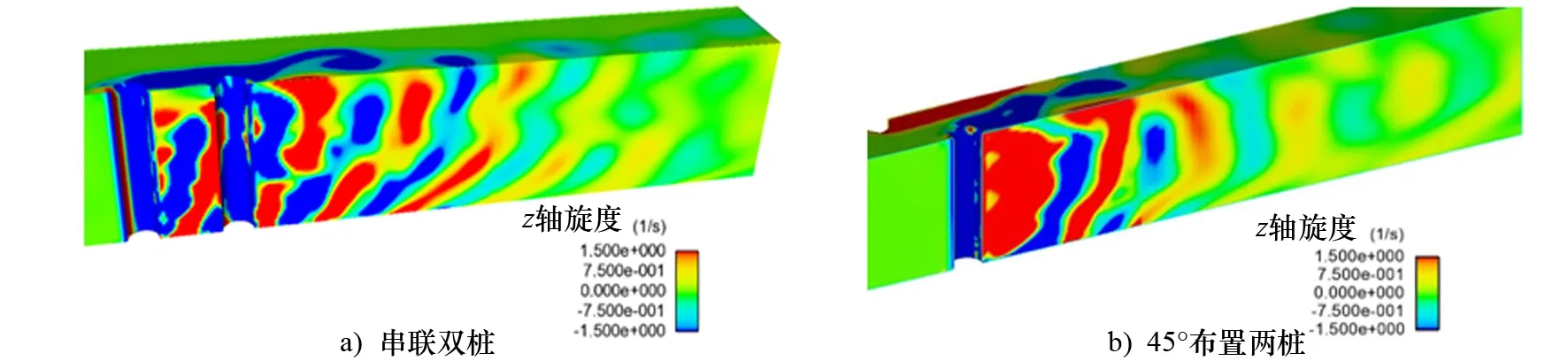
图16 双桩桩周三维涡量场分布

5 结 论

本文通过构建三维数值水槽模拟在单向流作用下不同间距、不同迎流角度布置的双桩基础周围流场的特征，为进一步研究群桩基础周围的冲刷奠定基础。主要结论与成果如下：

(1) 当并排双桩的间距为2D时，桩体阻碍作用明显，桩前流速降低并发生壅水，上部流速大而底层流速小，部分水流沿桩身向下流动。双桩中间流线未发生明显变化，相较于双桩外侧更为稳定。双桩尾涡在竖直方向上逐渐分离，其脱落形态类似龙卷风，底部涡的脱落晚于上部涡，且脱落位置大致为1倍桩径水深处，底部涡影响范围小于上部涡。

(2) 双桩间距的改变影响桩后漩涡脱落的频率与发生区域。当双桩间距0.5D时，涡流在内部剪切层发展，漩涡在桩后一段距离才发生扩散、脱落。当间距增大到3D后，各桩桩后涡量分布较为独立，双桩交互影响显著减弱。

(3) 串联布置的双桩，前桩的剪切层发展成熟向下输送，撞击下游的圆桩，形成涡流脱落的流态，前后两桩的干扰以尾流效应为主，漩涡脱落呈现反对称，且底部干扰较上部更为明显；与流向成45°布置的两桩，其存在前后和上下2种剪切层，以及面临前桩尾流的共同作用，涡量分布复杂。