极限波浪作用下半潜式平台水动力特性
2019-01-09,,,
, , ,
(1. 大连理工大学 船舶工程学院, 辽宁 大连116024;2. 高新船舶与深海开发装备协同创新中心, 上海 200240;3. 大连海洋大学 海洋与土木工程学院, 辽宁 大连 116023)
0 引 言
随着海洋平台向深水领域进军,具有相对投资小、工作水深范围广、甲板可变载荷大以及多种工作功能等优点的半潜式海洋钻井平台得到了更广泛的发展。半潜式海洋钻井平台最大工作水深达到几千米。平台工作环境较为恶劣,需在极端海况条件下对平台进行精准定位,即需计算平台载荷、运动响应和系泊绳系泊力。
半潜式平台包含立柱、浮筒和横撑等柱状构件。大构件基于波浪势流理论计算,小构件基于Morison方程理论计算。SÖYLEMEZ等[1]通过数值模拟对比试验发现两者计算结果在浪频率主要范围内较为吻合。CLAUSS等[2]通过研究波浪非线性问题,验证时域数值模拟更贴近试验值。史琪琪等[3]建立时域系泊耦合模型,发现当运动模态相同、吃水变化时,运动幅值响应算子(Response Amplitude Operator,RAO)曲线形状相似。姜宗玉等[4]通过深水半潜式平台系泊系统时域研究指出,半潜式平台在水平运动方向上低频效应显著,在垂荡上波频效应比较明显。霍发力[5]考虑水深对半潜式平台运动响应和设计的影响。
本文应用ANSYS软件的AQWA模块对某深水半潜式平台进行频域和时域分析,研究平台的水动力特性;对在不同浪向下计算出的设计波进行波浪载荷的映射,为平台整体结构设计提供参考。
1 理论介绍
1.1 水动力计算理论
在半潜式平台水动力计算中,假设流体无黏、无旋、不可压缩,基于势流理论计算分析。速度势函数满足拉普拉斯方程,考虑自由水面和不可穿透的物面边界条件,采用满足自由水面条件的频域计算格林函数,采用边界元法计算速度势函数。按照Bernoulli公式计算物体湿表面上的压力分布。
引入在简谐波作用下平台运动的系统线性假定,进一步确定平台的运动响应。在单位波幅的规则简谐波作用下,浮体的响应函数为
R(ω,t)=ARe{|H(ω)|exp[i(ω t+φ)]}
(1)
式中:A为入射波波幅;ω为谐波圆频率;t为时间参量;j为谐振初始相位;H(ω)为传递函数RAO。
不规则波计算采用JONSWAP谱,其谱密度表达式[6]为
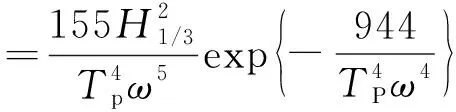
(2)
式中:H1/3为波高有义值;Tp为波谱周期;σ为波峰因子;γ为峰值增长因子。
结构物的运动响应谱计算公式为
Sr(ω)=Sω(ω)|H(ω)|2
(3)
式中:Sω(ω)为波谱密度函数;Sr(ω)为平台运动响应谱函数。基于以上理论,用谱分析方法可以预报平台在某工况下的运动响应。
1.2 系泊系统耦合作用
对于海洋结构物而言,除了考虑自由状态下的运动响应外,当有系泊时还须考虑系泊系统对结构物主体的作用。因此,需建立平台和系泊耦合数值计算模型,计算平台在6个自由度上的刚体运动方程和系泊系统、系泊力组成系统的运动与动力方程,系统的运动耦合方程[7-8]为
M+Max″(t)=Fwf(t)+Fc(t)+Fw(t)+Fm(t)+Fd(t)+Fh(t)
(4)
式中:M为质量矩阵;Ma为附加质量矩阵;x''为加速度;Fwf为波浪力;Fc为流载荷;Fw为风载荷;Fm为系泊力;Fd为阻尼力;Fh为静水回复力。
1.3 确定设计波
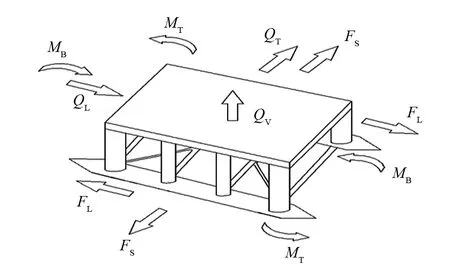
图1 半潜式平台的水动力响应参数
设计波,即对波高、波浪入射角、相位角、周期等波浪参数进行任意组合而获得的使平台处于最危险工况时的最大波浪载荷。 一般有3种确定方法:确定性、随机性和长期预报的设计波方法。李红涛等[8]对半潜式平台整体结构设计的波浪载荷研究表明:确定性设计波法计算简单,设计波高也偏大,适合设计初期的估算;随机性设计波法的计算结果与长期预报结果较为接近。本文采用确定性设计波法确定不同浪向下的设计波,并计算对应波浪载荷。
根据DNV规范[9]建议,在半潜式海洋平台整体结构设计中,应该考虑各种波浪载荷参数组合(见图1)引起的波浪特征载荷计算工况[10],见表1。

表1 半潜式平台波浪特征载荷工况
确定性设计波法是根据平台不同计算工况,利用波陡进行不同的规则波波高和周期组合,得到最危险组合工况。具体计算思路如下:
(1) 由平台主要尺度以及表1的载荷工况,确定在7个特征载荷工况下的波浪入射角和周期。
(2) 计算在不同工况下的RAO。规则波频域计算周期范围推荐选取3~25 s,在预计特征周期TC附近周期应该适当加密,推荐周期间隔为0.2~0.5 s,以获得较为准确的TC,并在较为准确的TC附近再次加密周期获得更准确的TC,远离TC的周期间隔可适当放大,推荐间隔为1~2 s[11]。
(3) 规则波波陡S计算公式为
(5)
式中:g为重力加速度;H为规则波波高;T为规则波周期。规则波波陡通常不必超过以下公式确定的数值
(6)
式中:H100为百年一遇规则波最大设计波高。
(4) 由式(6)确定规则波波陡,再由式(5)可得不同的规则波波高和周期组合情况(H,T)。
(5) 根据不同组合的规则波波高值与在对应特征工况下的RAO之积可计算特征响应。
(6) 计算得到最大特征响应值下的波高和周期组合(H,T),即为平台整体结构设计所采用波的波高和周期。
2 半潜式平台及其系泊系统
2.1 平台模型
平台整体关于中纵剖面和中横剖面对称,工作水深为1 500 m,平台由双浮箱、4立柱、上层甲板组成。根据平台的初步设计方案及其主要参数(见表2),建立平台的三维数值模型,如图2和图3所示。

表2 平台主尺度

图2 湿表面网格单元模型 图3 整体有限元模型
2.2 系泊参数
平台采用分布式系泊系统进行定位,系统包含12根悬链线系泊绳,每3根为1组,分为4组对称布置,系泊的预张力倾角α取75°。图4为该系泊系统布置方案,表3为系泊绳的设计参数。
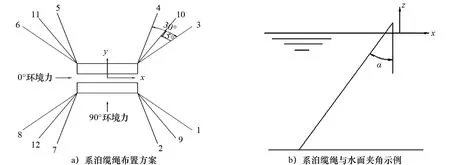
图4 系泊系统布置方案

缆索组成长度/m直径/m失效载荷/kN轴向刚度/kN湿重/(kg·m-1)钢链1 5000.14616 37363 300372.0聚酯缆2 4760.27018 95324 46410.8
2.3 海洋环境
本算例计算工况取中国南海的海况参数,选取风浪流同向,且与平台纵向正方向夹角分别为0°和90°,模拟该平台在中国南海一年一遇(即作业工况)和百年一遇(即自存工况)海况下的运动状态,分析其运动响应。风浪流具体参数见表4。

表4 海洋环境参数
表5为实际平台在作业和自存海况下参数的详细介绍。

表5 平台在作业、自存海况下主要参数
2.4 数值计算
应用ANSYS绘制平台三维水动力数值计算模型,进行网格自动划分,调用AQWA读取模型节点信息;通过Mechanical模块计算得到的模型质量、重心高度和转动惯量等模型参数设置在计算卡片中,进行水动力计算;调用AQWA-LINE计算各个自由度方向上的附加质量、辐射阻尼和运动响应函数等;调用AQWA-DRIFT进行时域分析;使用AQWA-GS进行计算结果处理;最后将设计波参数通过AQWA-WAVE映射在平台上,通过Mechanical模块得到平台所受波浪载荷云图,为平台整体结构设计提供参考。图5为计算过程的流程。
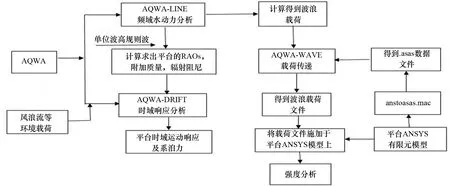
图5 计算流程
3 数值结果分析
3.1 频域结果分析
平台频域分析主要包括附加质量、辐射阻尼、各自由度上运动响应算子RAO等,AQWA采用Cumins法将频域计算结果转换引入时域分析模块,便于进行时域分析。平台计算的附加质量在6个自由度方向上的值如图6所示。
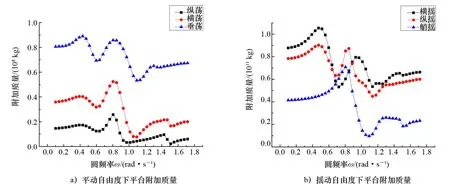
图6 各自由度下平台附加质量
图7为半潜式平台在规则波中6个自由度方向上的辐射阻尼值。
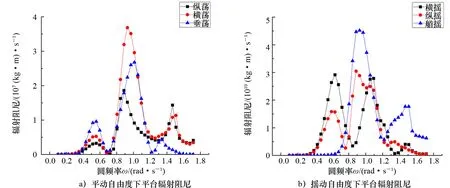
图7 各自由度下平台辐射阻尼
从图6和图7可知:垂向附加质量>横向附加质量>纵向附加质量,这是由于平台垂向面积>横向面积>纵向面积。在6个自由度方向上,附加质量在低频和高频范围内较为稳定,而在0.6~1.2 rad/s(5~10 s)频率范围,即常见波浪周期范围,呈曲线且出现波峰、波谷,曲线波动剧烈。辐射阻尼也出现同样规律,且在摇晃方向上的辐射阻尼峰值远大于在水平及垂向上的辐射阻尼峰值。
平台在各个自由度方向上的运动响应RAO如图8所示。
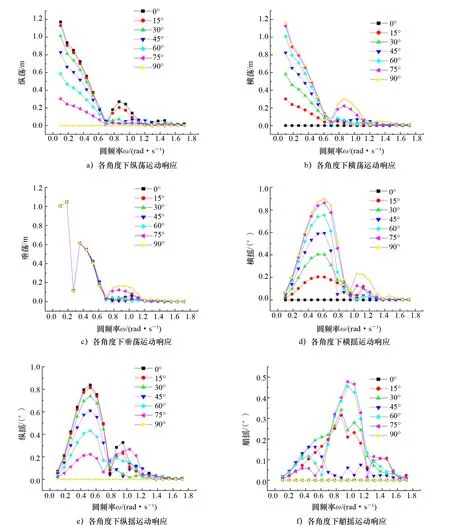
图8 各角度下平台运动响应
平台在高频区域(ω≥0.7)响应算子RAO较小,运动特性较好;平台的固有垂荡周期大约为20.9 s(圆频率ω=0.3时);平台在纵横荡以及纵横摇上运动具有一致性,体现了平台的结构对称性;在0°浪向下,平台的纵荡、纵摇响应较大,在90°浪向下,平台的横荡、横摇响应较大。
3.2 时域耦合结果分析
半潜式平台承受来自不同方向的风浪流载荷。在同一时刻,风浪流三者的方向不一定相同,但是三者同向的情况最危险,因此本算例假定三者同向。分别计算在0°、90°两种工况下平台的6个自由度方向的时历曲线,计算时假定平台的初始位置位移、速度和加速度均为零。模拟历时取5 000 s。图9和图10显示的是浪向分别取0°和90°时,平台在工作工况和自存工况基于一阶RAO计算的平台纵荡、横荡运动与包含二阶慢漂运动的平台纵荡、横荡运动幅值对比。其中,基于一阶RAO计算的平台纵荡、横荡的运动幅值约为 -1~1 m,而在工作状态下实际纵荡运动范围大致在-5~30 m,横荡运动范围大致为0~15 m;在自存状态下实际纵荡运动范围在-10~80 m,横荡运动范围大致为0~40 m。由此可见,二阶慢漂运动是平台水平方向运动的主要因素。
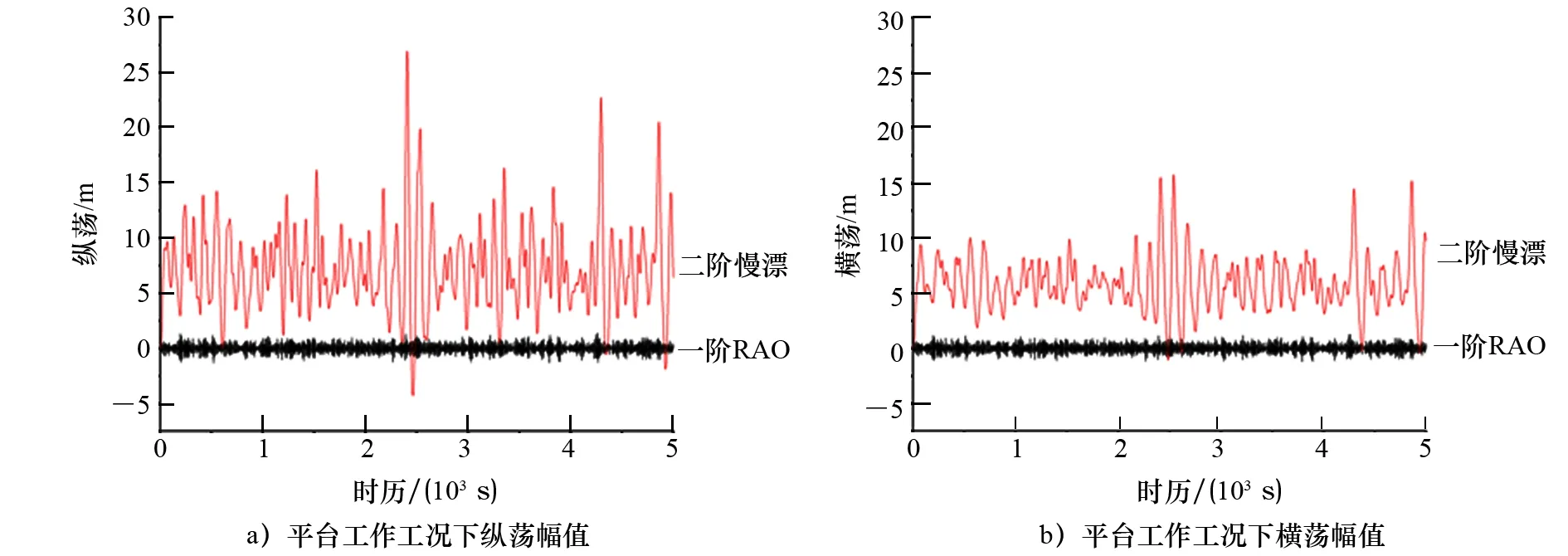
图9 平台工作工况下纵荡、横荡幅值
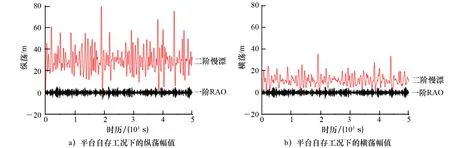
图10 平台自存工况下纵荡、横荡幅值
图11~图13显示的是环境力分别取为0°和90°时平台在工作工况和自存工况下的运动响应谱。可以看出:平台的纵横荡、纵横摇运动响应谱谱峰都集中在0.1 rad/s,这是由于平台在纵横荡、纵横摇运动方向上的运动周期均远离波浪频率周期,所以平台在水平方向和纵横摇方向上体现低频运动特性;垂荡运动响应谱峰集中在0.3 rad/ s,并且在自存工况下的谱峰峰值远大于在工作工况下的峰值,这是由于平台在工作工况下的低频响应与波频运动响应处于同数量级,因此低频运动显著,而在自存工况下低频运动响应较波频运动响应小,此时低频运动可以忽略,主要体现波频运动特性。
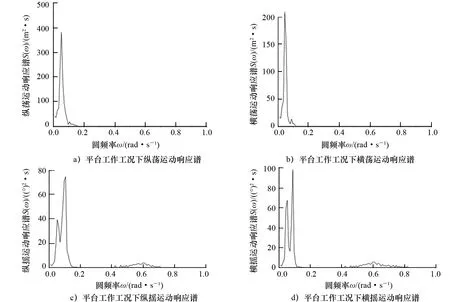
图11 平台工作工况下纵横荡、纵横摇运动响应谱

图13 平台工作工况、自存工况下垂荡运动响应谱
图14和图15为平台在工作工况和自存工况下的各自由度运动响应的低频与波频分量对比。在两种工况下,0°入射时运动响应主要体现在纵荡、纵摇以及垂荡方向上;90°入射时运动响应主要体现在横荡、横摇以及垂荡方向上。对比低频与波频的RAO标准差,低频主要体现在纵横荡以及纵横摇自由度上。对比两种不同工况,在工作工况下的低频垂荡与波频垂荡标准差处在同数量级,而在自存状态下的低频垂荡明显小于波频垂荡。因为平台正常工作时的固有垂荡周期较大,远离波浪周期,引起垂荡共振区域较狭窄且小于波频,此时平台波浪力主要体现为二阶力,平台低频特性较为明显;平台处于自存工况下时,固有垂荡周期在波浪周期范围内,将可能会与波浪频率发生共振,此时平台低频特性不明显,可以忽略。同样地,分析上述的工作和自存工况下的运动响应谱曲线也可得到相似规律。
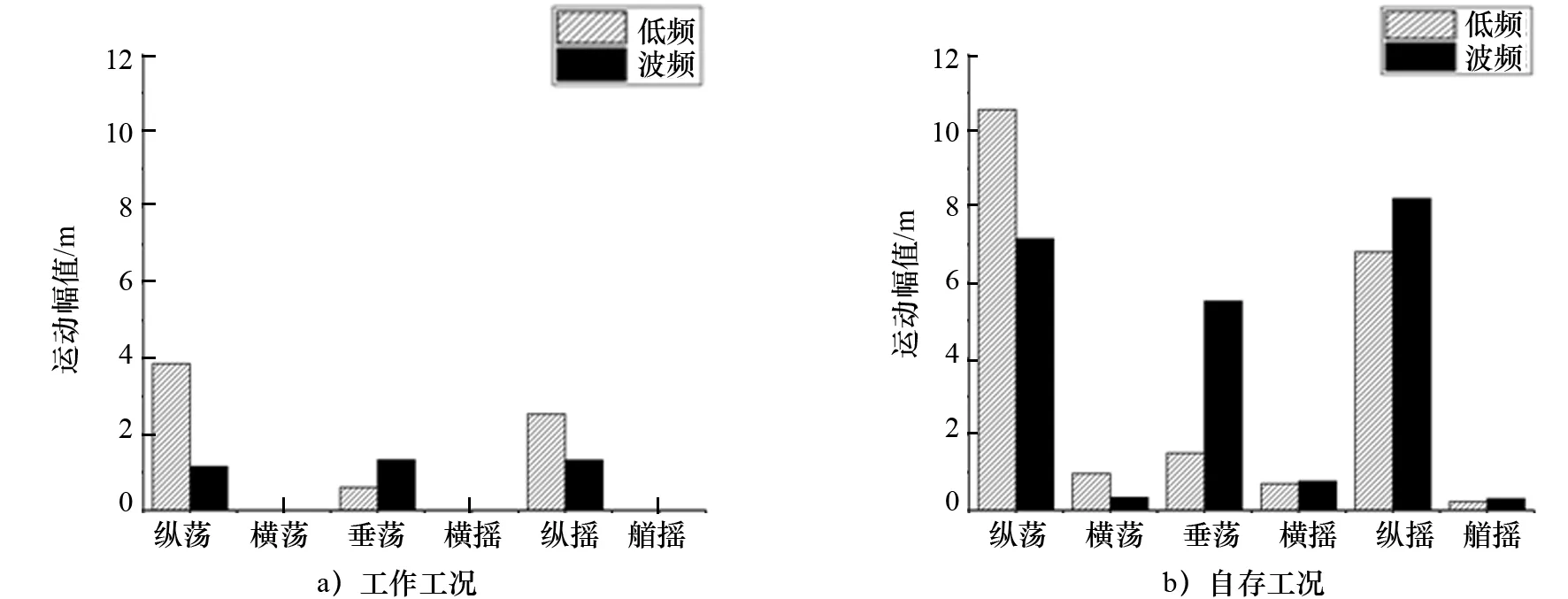
图14 平台在0°入射角时工作、自存工况下的低频与波频运动响应标准差
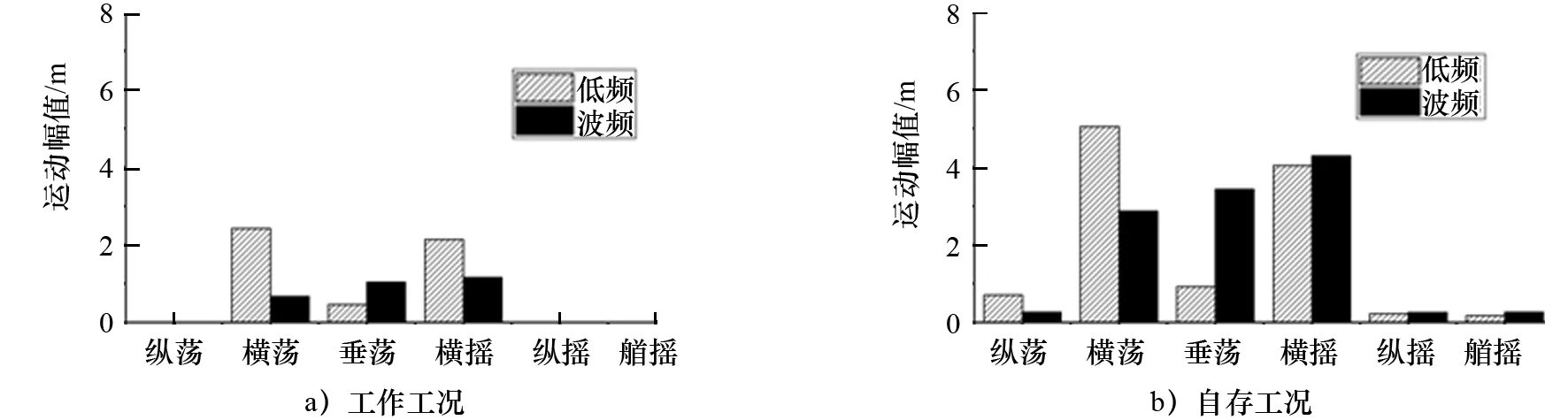
图15 平台在90°入射角时工作、自存工况下的低频与波频运动响应标准差
图16为平台系泊绳在不同工况下的受力情况,可以看出在0°浪向时,编号5、6、7、8、11、12的系泊绳承受较大拉力;在90°浪向时,编号1、2、7、8、9、12的系泊绳承受较大拉力。
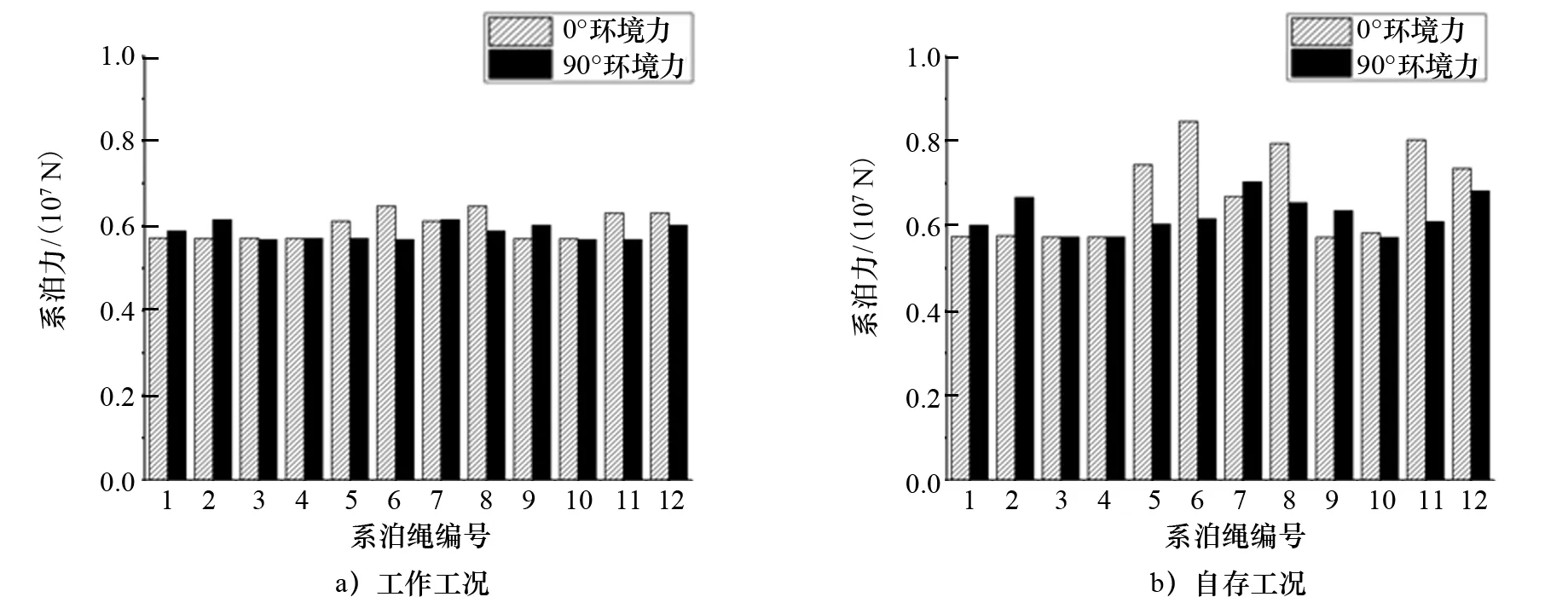
图16 平台在工作工况、自存工况下各系泊绳系泊力
表6为对不同工况、不同入射角下的最大系泊力的校核,结果表明各系泊绳均大于API-RP-2SK 设计规范的安全因数1.67,因此系泊绳满足强度要求。
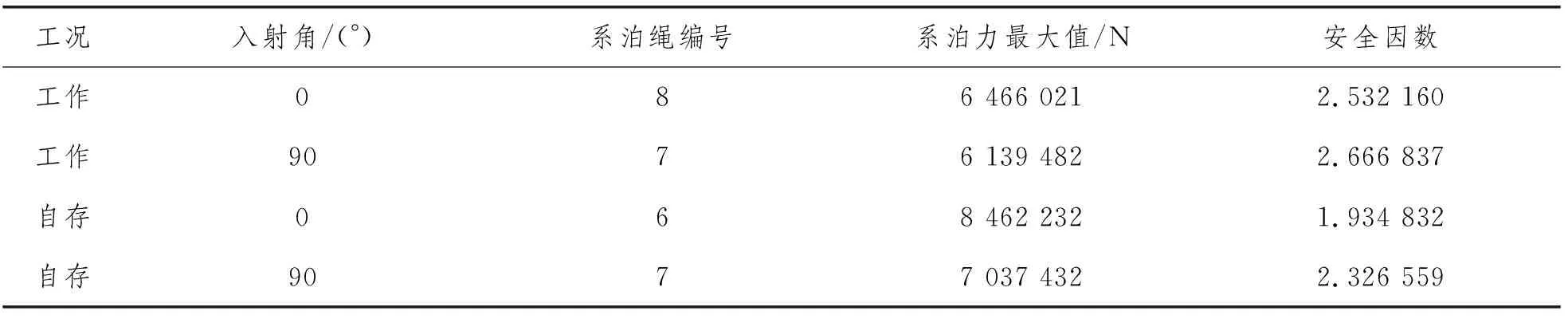
表6 最大系泊力校核
3.3 确定设计波
在本算例中,采用确定性设计波法提取各波浪角下的设计波参数,将得到的设计波载荷映射在平台上,得到平台整体结构所受波浪载荷云图。设计波参数及波浪载荷见表7。
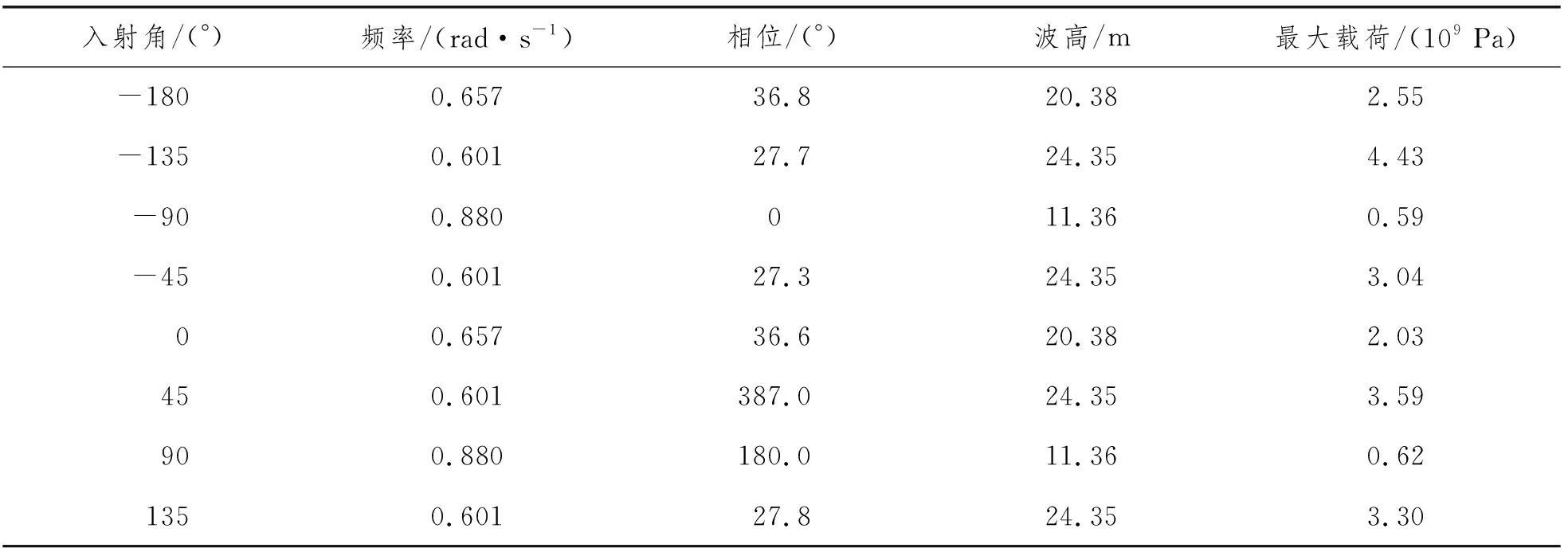
表7 不同工况下设计波及波浪特征载荷
提取各浪向下的设计波,将其映射在平台上,得出设计波对应的波浪载荷。图17为在0°浪向下的平台受到的波浪载荷等效压力云图。从图17可以看出,波浪载荷主要作用在浮箱处、立柱与浮箱连接处以及横撑与立柱连接处,因此在平台结构强度设计时需对这些应力集中处进行加强,以满足结构强度要求。
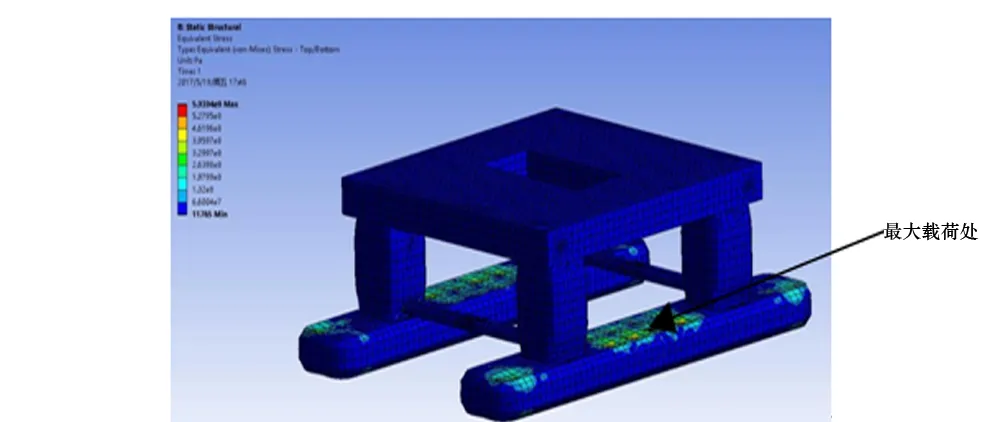
图17 0°浪向下波浪载荷等效压力云图
4 结 论
对半潜式平台进行频域和时域系泊耦合分析,得到平台在不同工况下的运动和系泊力响应以及设计波和波浪载荷,对比分析数据得出如下结论:
(1) 平台在高频范围内响应小,运动特性较好,在纵横荡以及纵横摇方向上具有一致性,这是因为平台尺度的纵横比接近1,平台截面趋于方形,此时的纵、横初稳心高,彼此接近。
(2) 平台在水平方向上的慢漂运动幅度远大于一阶运动幅度,二阶慢漂对系泊影响很大,因此需降低慢漂运动幅值以减小系泊力,比如增加平台的附加阻尼等。
(3) 平台在水平方向上低频运动特性显著,而在垂荡方向上体现了波频特性,这主要是由两个方向的刚度和回复力差别引起的,即平台垂向回复力很大导致垂向系统刚度很大,结构的响应频率集中于高频,水平方向则与其相反。
(4) 平台的运动响应谱和低频与波频运动响应对比结果进一步证实,平台在水平方向上的低频特性与在垂荡方向上的波频特性。
(5) 通过确定性设计波法确定在不同浪向下的设计波,通过接口命令将波浪载荷映射在平台整体结构上,可得到平台整体所受波浪载荷云图,从水动力分析和波浪载荷传递两个角度对海洋平台的初步设计提供参考。
