四足机器人斜面运动规划及控制研究

杜威，杨忠，许昌亮，张辉斌

(南京航空航天大学 自动化学院，江苏 南京 210016)

0 引言

四足机器人(quadrupedrobot，QR)属于足式机器人，相对于履带式和轮式机器人，具有机动性好、环境破坏程度小、主动隔振等优点，应用前景良好。该型机器人涉及力学、机械学、生物学、计算机、人工智能等多学科，相关技术一直是国内外机器人领域研究的热点之一。以美国卡耐基梅隆大学的波士顿动力实验室为代表，2005年发布了BigDog大狗机器人，又先后推出了如AlphaDog、LittleDog、Cheetah等产品，引起行业内的广泛关注。

能否在不同地形条件下实现平稳运动，是一个机器人是否具有实际使用价值的评判标准。斜面是自然界中常见的地形，一些崎岖的地形也可以等效为斜面。因此，研究四足机器人在斜面上的运动控制具有重要意义。经典控制和现代控制在设计过程中一般是基于被控对象的精确数学模型。对于四足机器人来说，因其具有非线性、高耦合、模型复杂等特点，采用传统的控制理论和方法往往存在局限性，难以取得满意的控制效果[1]。模糊控制是建立在模糊集合论基础上的一种基于语言规则与模糊推理的控制理论，在控制非线性、高耦合及参数和结构不确定的复杂过程中具有较好的控制效果。

在对四足机器人运动学建模的基础上，从机身姿态、足端轨迹以及步态周期3个方面分析并设计了四足机器人斜面运动方式，并建立了一种应用于四足机器人斜面运动的模糊控制系统，最后通过仿真实验证明所设计的控制系统具有较好的控制效果。

1 运动学建模及斜面运动规划

1.1 运动学建模

四足机器人简化模型由机身、大腿和小腿等构件组成，构件间由旋转关节连接，连接部分分别为负责横向摆动的臀关节、负责上下抬腿的髋关节以及膝关节。臀关节负责内外摆，实现机身左右摆动；髋关节和膝关节分别负责大腿和小腿的抬起和落下，实现机器人前后运动。四足机器人采用内膝肘式设计，以前进方向为基准，将左前腿、左后腿、右前腿以及右后腿分别命名为LF、LH、RF、RH。关节连杆结构见图1。

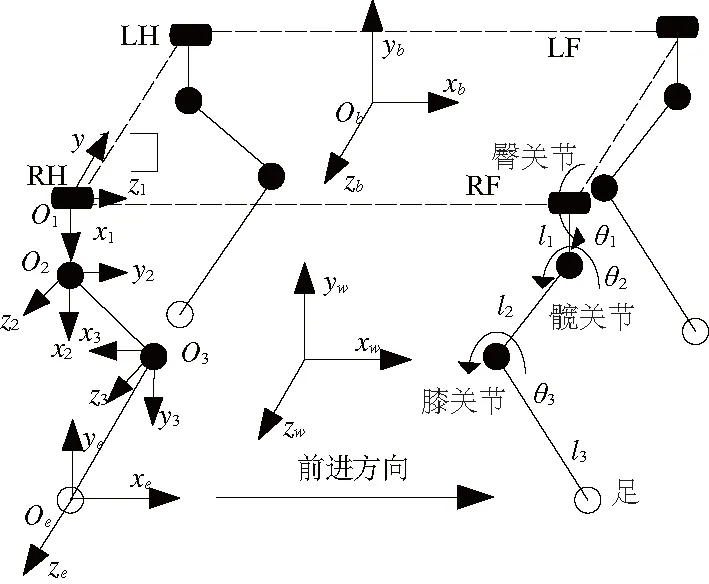
图1 四足机器人的关节连杆结构及坐标系定义

采用D-H参数法[2]确定机器人各构件间的位姿关系。四足机器人的坐标系定义示意如图1所示。以RH为例，定义世界坐标系{W}，机身坐标系{B}，以及足端坐标系{E}。同时定义臀关节坐标系{1}，髋关节坐标系{2}，膝关节坐标系{3}，以上3个坐标系坐标原点分别位于3个关节位置，坐标系方向由D-H法规范确定。

基于上述四足机器人的关节连杆结构以及坐标系定义，可从足端坐标系沿各关节连杆依次向机身坐标系进行齐次变换，得到足端坐标系到机身坐标系的转换矩阵：

Tbe=Ab1A12A23A3e

(1)

式中：Ab1,A12,A23,A3c为坐标系{B}、{1}、{2}、{3}、{E}之间的齐次变换矩阵。由D-H参数可确定上述各矩阵，进一步可以得到：

(2)

式中：si=sinθi,ci=cosθi,sij=sin(θi+θj),cij=cos(θi+θj)；l1、l2、l3与θi为图1中所示的各连杆及对应角度；(a,b,c)为坐标系{1}的坐标原点相对于机身坐标系{B}的位置。下标i、j分别取1、2、3。

由式(2)可以得出:

(3)

(4)

矩阵Rbe反映了足端坐标系到机身坐标系的旋转关系，三维矢量Pbe反映了足端在机身坐标系中与质心的位置关系，两者共同体现了机器人足端的位姿。

1.2 斜面运动规划

斜面运动规划的关键是保证四足机器人在行走过程中的稳定性。四足机器人本身具有较好的结构稳定性，但在斜面运动过程中，由于受到重力的作用，机体姿态以及运动步态的变化都会对其运动的稳定性造成影响[3]。本节从机体姿态、足端轨迹以及步态周期3个方面对四足机器人的斜面运动规划进行研究。

四足机器人在斜面运动时的机体姿态一般有水平姿态以及平行于斜面姿态两种[4]，如图2所示。相对于水平姿态而言，平行于斜面姿态具有前后腿的运动范围相当、足端轨迹规划简单、稳定裕度高等优势[4]，故四足机器人在斜面运动过程中采用平行于斜面姿态。

图2 四足机器人两种机体运动姿态

常用的足端轨迹曲线包括抛物线、心形线、摆线等。本文选取一种零冲击足端轨迹的规划方法，其具有冲击小，曲线圆滑，落地角度垂直不易打滑等优点[5]，在坐标系{W}下，水平与竖直方向的足端轨迹数学表达式分别如式(5)与式(6)。式中，S为步幅，H为抬腿高度，Tm为摆动相周期。

(5)

(6)

步态选择方面，选取稳定性高的三角步态作为四足机器人在斜面上的运动步态，并采用LF-RH-RF-LH的腿部运动顺序以获得最优的稳定裕度[6]。本文的运动步态时序图如图3所示。其中，黑色矩形表示腿部处于支撑相，白色矩形表示腿部处于摆动相。

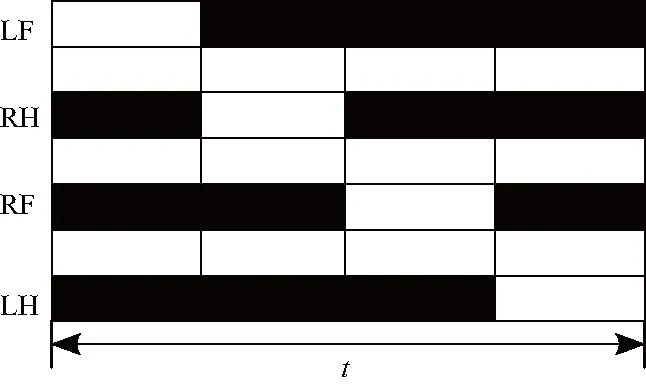
图3 三角步态运动时序

2 斜面运动控制设计

2.1 模糊控制器设计

用模糊控制方法解决控制问题时,重点在于对控制中所可能出现的各种情形加以分析,依据控制者的经验和先验知识,寻求解决的一般方法,并用模糊控制规则的形式加以体现,模糊控制的精度将依赖于模糊控制规则制定得是否合理和详尽[7-8]。

图4是开环斜面运动过程中的机身滚转角变化仿真图。1.3s与2.1s分别是第一个运动周期内RH与LH处于摆动相的时刻，可以看到这两个时刻的机身滚转角绝对值较大。观察机器人的爬坡过程，可以发现RH与LH处于摆动项时，机器人机身会发生明显倾斜，即RH处于摆动相，机身明显向右倾；LH处于摆动相，机身明显向左倾。现做如下处理：若机身右倾，令LH的臀关节角度减少、髋关节角度增加；若机身左倾，令RH的臀关节角度减少、髋关节角度增加。以上操作均可减少机身的滚转角度绝对值，使机身趋近水平位置。

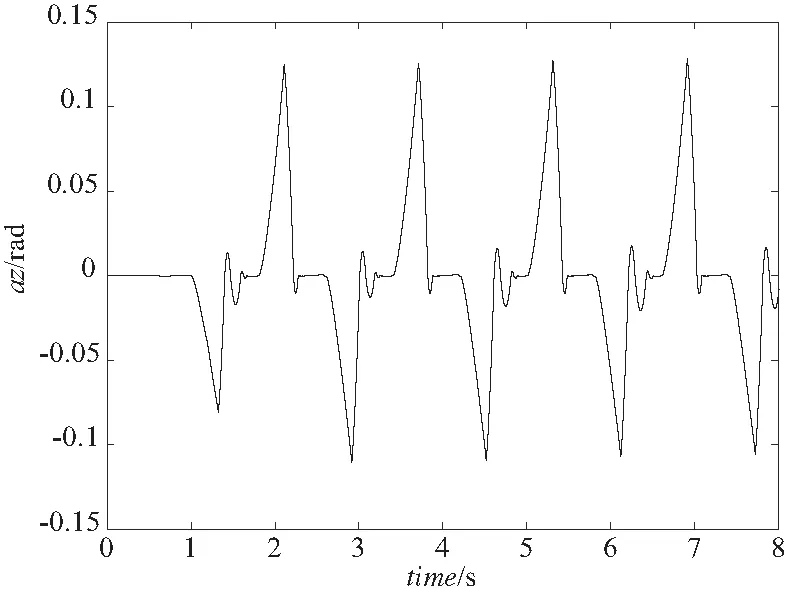
图4 开环运动过程的机身滚转角变化

基于以上分析，设计应用于四足机器人斜面运动的模糊控制系统。确定模糊控制系统为双输入四输出，四足机器人机身的滚转角(az)以及滚转角的变化率(wz)作为输入变量：

az∈X1=[-0.15,0.15] (rad)

wz∈X2=[-1,1] (rad)

LH的臀关节转动角度和髋关节转动角度(anglelh1、anglelh2)以及RH的臀关节转动角度和髋关节转动角度(anglerh1、anglerh2)作为输出变量：

模糊控制系统的结构图如图5所示。

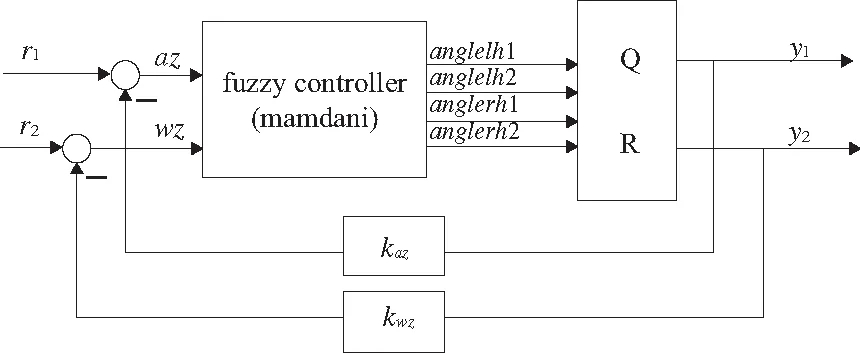
图5 模糊控制系统结构

2.2 论域和隶属度函数选择

选定滚转角az的模糊论域AZ={-2,-1,0,1,2}；模糊集为{NB,NS,Z,PS,PB}，分别对应“负大”、“负小”、“零”、“正小”、“正大”；隶属度函数种类选择为“trimf”，如示意图6所示。wz、anglelh1、anglerh1、anglelh2以及anglerh2的隶属度函数图像均与图6类似，后文仅给出隶属度函数对应的参数。

图6 az的隶属度函数

选定滚转角wz的模糊论域WZ={-2,-1,0,1,2}；模糊集为{NB,NS,Z,PS,PB}，分别对应“负大”、“负小”、“零”、“正小”、“正大”；隶属度函数种类选择为“trimf”，隶属度函数参数分别为：[-3, -2, -1] ，[-2, -1, 0] ，[-1, 0 ,1] ，[0, 1, 2] ，[1, 2, 3] 。

anglelh1、anglerh1、anglelh2以及anglerh2四者的论域与隶属度函数设置相同。对应论域分别为ANGLELH1、ANGLERH1、ANGLELH2、ANGLERH2；论域内容均设置为{0,1,2,3}；模糊集为{Z,S,M,B}，分别对应“零”、“小”、“中”、“大”；隶属度函数种类选择为“trimf”，隶属度函数参数为[-1, 0, 1] ，[0, 1, 2] ，[1, 2, 3] ，[2, 3, 4] 。

2.3 模糊规则设计

根据2.1节的分析，对于所述双输入四输出的模糊控制器采用以下的条件语句来描述控制规则：

If(Aisa)and(Bisb)then(Cisc)and(Disd)and(Eise)and(Fisf)

对于本文中应用于四足机器人斜面运动的模糊控制器，设计规则如下：

规则1：若四足机器人的滚转角(az)为正大(PB)且滚转角的变化率(wz)为正大(PB)，则LH的臀关节转角(anglelh1)为零(Z)且LH的髋关节转角(anglelh2)为零(Z)且RH的臀关节转角(anglerh1)为大(B)且RH的髋关节转角(anglerh2)为大(B)。

依照同样的方法写出其他规则，可以得到模糊控制规则表，如表1所示。表中LH1、LH2、RH1、RH2分别表示anglelh1、anglerh1、anglelh2、anglerh2。

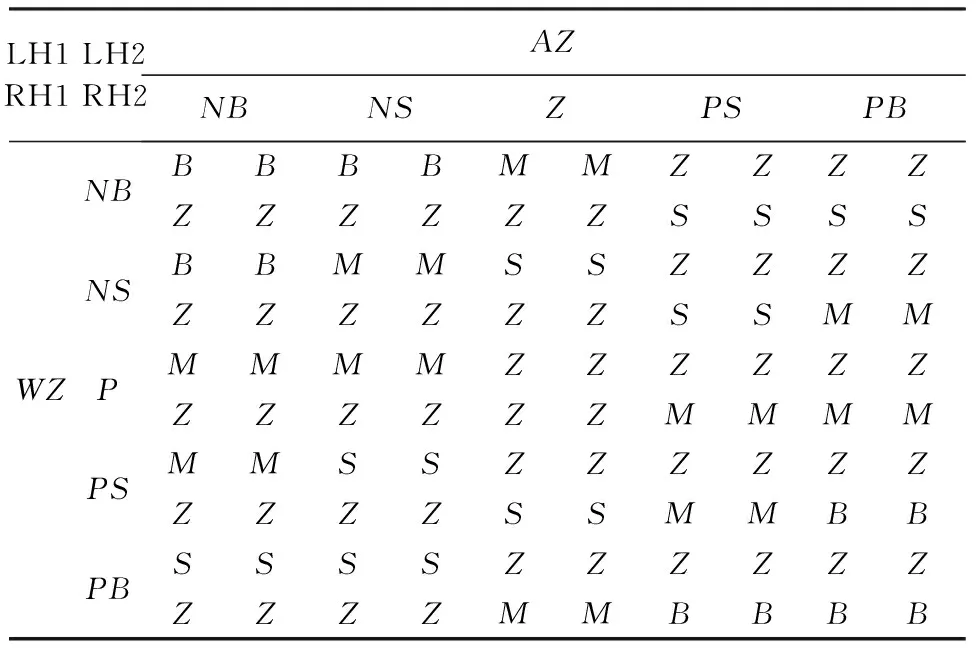
表1 模糊控制规则

3 仿真实验验证

仿真实验采用Matlab与Adams的联合仿真方式[9]。在Adams中建立四足机器人的三维模型，在Matlab中建立四足机器人的控制系统，通过使用Adams/control模块建立两者间的数据通信通道。

需要说明的是，为减少Matlab与Adams之间交换的数据量，在联合仿真过程中仅针对LH与RH的臀关节与髋关节进行数据交互。在开始仿真前，根据第一章规划的斜面运动方式，预先设计开环状态下所有关节的运动情况，并通过SPLINE函数导入到Adams模型中的对应关节。仿真开始后，控制器生成的控制信号将会叠加在4个被控关节角之上，形成新的关节角度以驱动模型运动，完成联合仿真[10]。

四足机器人机身及其他关节连杆的材料均选择为铝，密度为2.74e-6kg/mm3。为简化模型，机身设计为长方体，长为300mm，宽为75mm，高为20mm；大小腿均设计为圆柱体，高为120mm，底面半径为12.5mm；斜面设计坡度为5°，静摩擦系数为0.3，动摩擦系数为0.5。运动规划方面，采用稳定性较高的三角步态，设置步幅为40mm，抬腿高度为50mm，运动周期为1.6s。

图7为四足机器人在一个运动周期内的行走过程示意图。图8为四足机器人分别在开环与模糊控制下运动过程的机身滚转角变化对比图。其中，虚线为开环运动状态下机身滚转角的变化情况，实线为经模糊控制后机身滚转角的变化情况。图9为坐标系下机身质心在斜面运动过程中的运动轨迹，模型运动方向为X轴负方向。

图7 四足机器人的运动过程

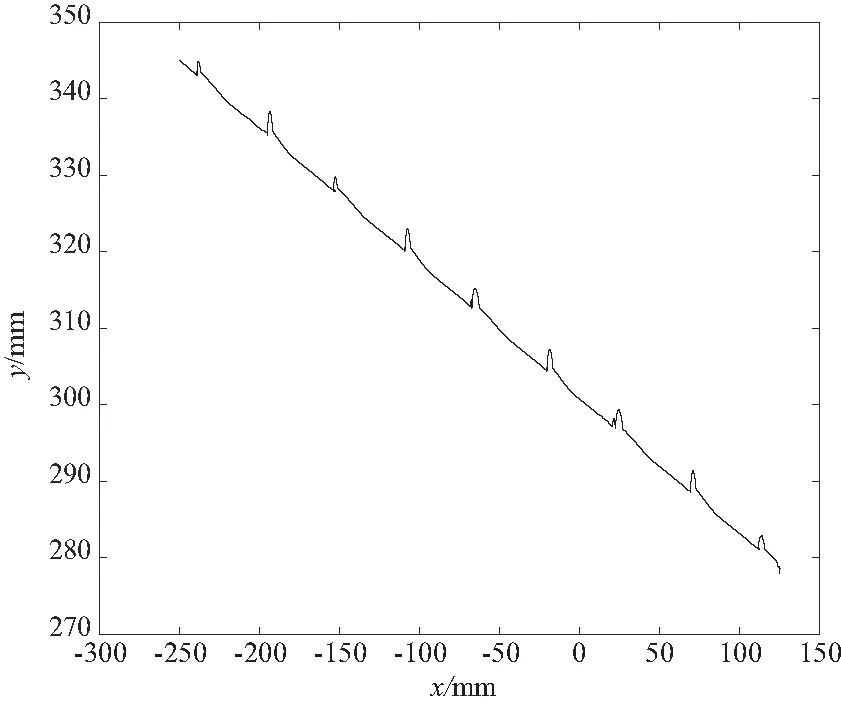
图9 坐标系下机身质心运动轨迹

4 结语

对四足机器人的斜面运动方式进行规划，提出了一种应用于四足机器人斜面运动的模糊控制方案。使用Matlab与Adams的联合仿真进行仿真实验，证明了所设计的斜面运动规划满足四足机器人的正常运动，所设计的模糊控制系统可以有效增加机器人的运动稳定性，达到较好的控制效果。