基于改进LSSVM算法的数控机床热误差建模研究

2019-01-08赵家黎李桥林黄利康

机械制造与自动化 2018年6期

赵家黎，李桥林，黄利康

(兰州理工大学机电工程学院，甘肃兰州 730050)

0 引言

随着制造业的飞速发展，数控机床越来越多地应用于各个行业之中，而且数控机床的精度要求也越来越高。数控机床的精度指标是直接影响加工精度的重要因素。数控机床误差是评价数控机床精度的主要指标，数控机床的误差一般可分为几何误差、热误差和力误差，其中热误差占有较大的比例。由于机床热误差具有非线性、交互性和耦合性等特点，传统的基于最小二乘原理的建模方法虽建模简单，但模型鲁棒性差，难以实现数控机床热误差高精度补偿[1-2]。近年来，国内外学者提出了神经网络、灰色理论、最小二乘支持向量机等多种热误差建模方法，但也存在一定的局限性，例如神经网络以及最小二乘支持向量机等建模方法虽可以将补偿精度提高数倍，但需大量的样本进行训练、建模复杂，且神经网络还易产生过学习或欠学习等问题；灰色理论预测等则对建模误差数据光滑性有严格要求，模型适应性不好，因此还需要寻求快速、高精度的建模方法[3-6]。

为此，本文提出了一种基于改进最小二乘支持向量机(LSSVM)的数控机床热误差预测方法，使用提升小波分解数控机床热误差数据，由此得到数控机床热误差的变化特征;然后采用最小二乘支持向量机对分解信号进行训练和预测，得到初步的预测结果;最后针对数控机床热误差有较大起伏波动的现象，对其进行修正和改进，达到提高预测精度的目的。

1 热误差数据处理方法

1.1 提升小波(LWT)分解原始数据

提升小波算法通过构造双正交小波函数，使用线性、非线性或空间变化的预测和更新算子进行提升变换，比较适合于数控机床热误差数据分析，可以有效获取其主要变化特征[7]。

提升小波分解的主要步骤如下：

1) 分裂:分裂是将数控机床热误差数据分割成相互关联的奇偶两部分，即ej-1(偶部分)和oj-1(奇部分)。

split(sj)=(ej-1,oj-1)

ej-1={ej-1,k=sj,2k}

(1)

oj-1={oj-1,k=sj,2k+1}

2) 预测:预测就是用ej-1预测oj-1，获取预测值P(ej-1)。实际值oj-1，与预测值P(ej-1)的差值dj-1反映了两者之间的逼近程度，称为细节系数或小波系数，对应于元信号sj的高频部分。预测过程为：

dj-1=oj-1-P(ej-1)

(2)

式中，预测算子P可用预测函数Pk来表示，函数Pk可取为ej-1中的对应数据本身，即：

Pk(ej-1,k)=ej-1,k=sj,2k

(3)

或取ej-1中对应数据的相邻数据的平均值，即：

Pk(ej-1,k)=(ej-1,k+ej-1,k+1)/2=(sj,2k+sj,2k+1)/2

(4)

3) 更新:经过分裂步骤产生子集的某些整体特征可能与原始数据并不一致，为了保持数控机床热误差数据的这些整体特征，需要一个更新的过程。将更新过程用算子U来代替，其过程为：

sj-1=ej-1+U(dj-1)

(5)

式中，sj-1为sj的低频部分。

与预测函数一样，更新算子也可以取不同函数。

Uk(dk-1)=dj-1,k/2

(6)

Uk(dk-1)=(dj-1,k-1+dj-1,k)/2

(7)

经提升小波分解，可将数控机床热误差数据分解为低频部分sj-1和高频部分dj-1;对于低频数据子集sj-1可以再进行相同的分裂、预测和更新，把sj-1进一步分解成dj-2和sj-2，…；如此下去，经过n次分解后，数控机床误热差数据sj的小波表示为{sj-n,dj-n,sj-n+1,…,dj-1}。其中sj-n代表了数控机床误热差数据的低频部分，而{sj-n,dj-n,sj-n+1,…,dj-1}则是功率数据从低到高的高频部分系列。具体的流程如图1所示，其中S为原始的数控机床热误差数据，A1、A2和A3为低频信号，D1、D2和D3为高频信号。

图1 提升小波分解的流程图

其反变换过程，即重构，也可以用替代的方式来计算：

ej-1=U(oj-1)

oj-1=P(ej-1)

(8)

sj=Merge(ej-1,oj-1)

P与U取不同的函数，可构造出不同的小波变换。经过Matlab仿真结果的分析，最终选用正交小波db2作为母小波，对功率序列进行三尺度分解。

1.2 基于最小二乘支持向量机的数据预测

在使用提升小波分解数控机床热误差数据后，采用最小二乘支持向量机(LSSVM)解决对每一层分解信号的训练和预测问题。最小二乘支持向量机方法是采用最小二乘线性系统作为损失函数，代替传统的支持向量机采用的二次规划方法，简化了计算复杂性的同时也可以保证预测结果的准确性[8]。而使用提升小波处理后的功率数据也更有规律，使用最小二乘支持向量机可以进一步提高预测精度。

设D={(xk,yk)|k=1,2,…,n}，其中xk∈Rn为得到的分解信号，yk∈R为输出结果。在权w空间中最小二乘支持向量机分类问题可以描述如下:

(9)

约束条件：

yk[wTφ(xk)+b]=1-ek,k=1,2,…,n

(10)

定义拉格朗日函数为：

L(w,b,e,α)=φ(w,b,e)-

(11)

式中，拉格朗日乘子αk∈R。

对上式进行优化，即对w,b,ek,ak的偏导数等于0。

(12)

上式可化为求解下面的矩阵方程：

(13)

即：

(14)

式中： Z=[φ(x1)Ty1,φ(x2)Ty2,…,φ(xn)Tyn]T

Y=[y1,y2,…,yn]

同时将Mercer条件代入到Ω=ZZT，可得：

Ωkl=ykylφ(xk)Tφ(xl)=ykylψ(xk,xl)

(15)

因此，式(9)的分解可以通过解式(14)和式(15)获得。

最小二乘支持向量机分类决策函数为：

(16)

式中:ψ(x,xk)是核函数，目的是从分解信号抽取特征，将分解信号中的样本映射为高维特征空间中的一个向量，以解决原始分解信号中线性不可分的问题。

在Matlab仿真中要求LSSVM的输入要作简单的归一化处理，归一化的公式为：

(17)

式中：xmax,xmin分别为训练样本集中输入变量的最大值和最小值；xi,yi分别为输入样本归一化前后的值。

2 数控机床热误差测量

相关研究表明，影响数控机床热变形误差的主要原因是主轴部件热变形误差，由于实验条件有限，并且这篇论文主要是验证LWT-LSSVM建模预测方法的可行性与准确性，所以只对数控机床部分发热部件进行实验分析和研究。

实验选取一台数控车床进行热误差预测建模研究。13个传感器分别放在13个关键的温度测点处，传感器的具体分布情况如表1和图2所示。

表1 传感器分布一览表

实验中，由于直接测量主轴热变形不太方便，所以用一根铁棒来代替主轴，把铁棒用磁性表座固定在主轴上，间接获得主轴径向与轴向变形。然后通过电涡流位移传感器测得这两个方向上的热误差数据。

图2 关键温度测点布置

经过4h运行，所测得的数控机床温度和热变形数据如图3和图4所示。

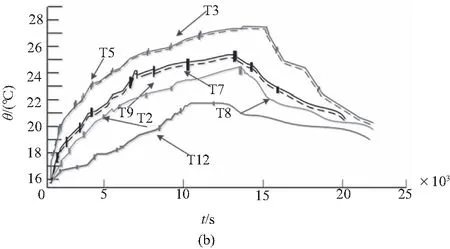
图3 机床关键点温度变化

图4 主轴径向与轴向热误差

LWT-LSSVM建模相比于其他建模方法的显著优势在于它所需要的训练数据量相对较少但精度很高，为提高运算速度，隔4min取一组数据，共取48组数据进行训练建模。

3 数控机床误差建模与对比分析

3.1 基于LWT-LSSVM的热误差建模

虽然LSSVM具有很强的泛化性能，但数控机床误差序列一方面具有一定的规律性，另一方面具有很强的随机性，是一种多频谱交叠的信号。用单一的LSSVM模型只能拟合出系统的非线性，而数据的非平稳性将使预测结果不太理想。利用提升小波的分频性能，可以提取相邻频带的不同信息。由于数控机床误差序列各频带内的信息相互正交，没有冗余信息，避免了因提升小波变换结果之间的关联造成分析的困难，因而能够实现较宽范围的带通分量处理。这样数控机床误差数据中的线性变化分量和高频随机分量，经提升小波分解后，其频谱将呈现明显的分离特征，有利于分开预测，因此初步建立LWT-LSSVM的数控机床误差预测模型[9]。

分析LWT-LSSVM的预测结果，会发现大多数采样点的预测精度已经达到要求，但还是有部分采样点会出现比较大的误差值，需要修正。为了进一步提高预测精度，采用误差预测的方法来校正预测结果。为了与初步预测结果统一，因此本文建立图5中的LWT-LSSVM的误差预测模型和校正模型。

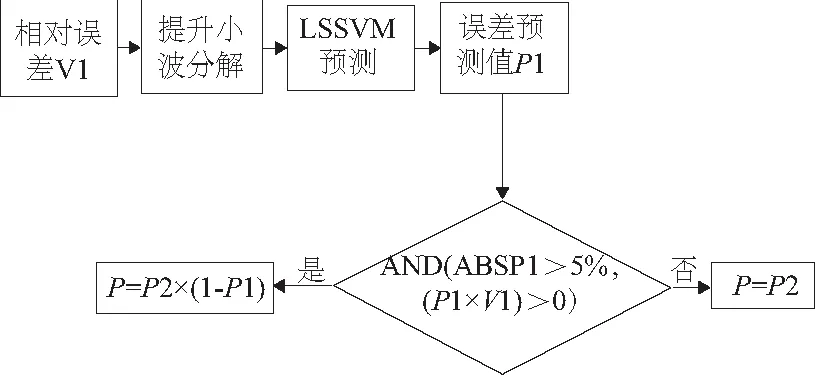
图5 误差预测模型

3.2 建模对比分析

为了比较基于LWT-LSSVM的数控机床热误差建模方法相对于其他方法的优缺点，本文同时给出了常用的基于最小二乘法支持向量机(LSSVM)回归建模的预测结果，两者比较如图6所示。从图中可以看出，基于LWT-LSSVM的预测方法获得的预测模型残差远小于最小二乘法支持向量机的模型残差，具有更好的模型预测效果。