雷达天线举升机构重载转动副偏差计算与可装配性分析
2019-01-08邱露孙启鹏邓傲然张炎李刚炎
邱露,孙启鹏,邓傲然,张炎,李刚炎
(武汉理工大学 机电工程学院,湖北 武汉 430070)
0 引言
装配偏差分析是为了找出偏差源与输出测点偏差之间的相对关系。目前偏差分析方法大体上可以分为基于刚体假设的偏差分析方法、基于线弹性体假设的偏差分析方法和单工位或多工位偏差分析方法[1]。不少学者对产品装配偏差进行了研究。Apley[2]等采用尺寸链偏差分析模型对零件偏差和夹具定位偏差之间的关系进行分析。但是对于装配关系相对复杂的产品,尺寸链关系难以建立。Cai等[3]运用坐标变换的方法对零件定位点、制造和位姿偏差之间的关系进行研究。此类基于确定性定位的偏差分析方法能解决尺寸链模型无法克服的空间复杂偏差分析问题,且可提高计算精度。
装配是产品制造过程中十分重要的环节,产品的可装配性体现了产品及其装配元件(零件或子装配体)容易装配的能力和特性,而可装配性评价是基于产品的设计阶段
考虑产品的可装配性、装配序列和路径等各因素,不仅可以为零件的设计公差提供修改意见,也可为产品的装配工艺流程提供技术指导。目前对产品可装配性评价的研究大多是定性分析,李元源[4]从装配单元、装配工艺和装配资源三类因素归纳了评价可装配性的三种指标:成本、技术和社会,并对产品的可装配性进行了模糊综合评价。但对产品可装配性进行定量分析的较少,而对于雷达天线举升机构中的重载转动副,相对于一般的销轴转动副结构更加复杂,其装配精度对整机的精度影响较大,因此成本、生产等评价指标并不是其进行可装配性评价的决定性影响因素,从质量和精度着手进行研究才是其需要考虑的重点。宋君侠[5]从装配公差分析模型提出了基于法兰盘装配实例的一种可装配性定量评价方法。以重载转动副为对象研究,该评价方法并不适用。基于上述分析,本文提出重载转动副可装配性的定量分析方法,通过装配偏差分析方法计算得到的结果判断重载转动副的可装配性,这将对转动副装配精度的研究提供理论基础。
1 雷达天线举升机构重载转动副
1.1 重载转动副结构特点
转动副在机械中被广泛应用,常见的转动副一般为简单的销轴连接。但是某型雷达天线重约3t,主要通过转动副承重,且举升机构工作速度较慢,因此雷达天线举升机构中转动副的工况是低速重载。简单的铰链连接强度无法满足工程实际,因而针对此服役环境采用一类复杂的重载转动副,本文所述重载转动副为重载机构的转动副,其结构示意图如图1所示。底座通过一对轴承与轴连接,轴与连杆的孔连接,轴承外圈与底座内孔为间隙配合。此处采用的轴承为30210型圆锥滚子轴承,主要是考虑到圆锥滚子轴承适用于低速重载机构,可以同时承受径向和轴向载荷。

图1 重载转动副结构示意图
1.2 重载转动副装配偏差与可装配性的关联
雷达天线举升机构中重载转动副连接着各构件,其产生的误差会影响到机构的误差,而重载转动副不同装配过程的可装配性评价更是关系到整机的装配精度。如果以零件的理想尺寸进行装配,重载转动副一定能够成功装配,但由于存在零件公差及装配间隙,装配偏差会在装配过程中传递与累积,从而影响装配结果,因此需要对重载转动副的可装配性进行分析。基于重载转动副装配实例,其可装配性分析流程如图2所示。通过计算后的装配累积偏差与零件配合特征产生的间隙进行比较从而对重载转动副的可装配性进行分析。
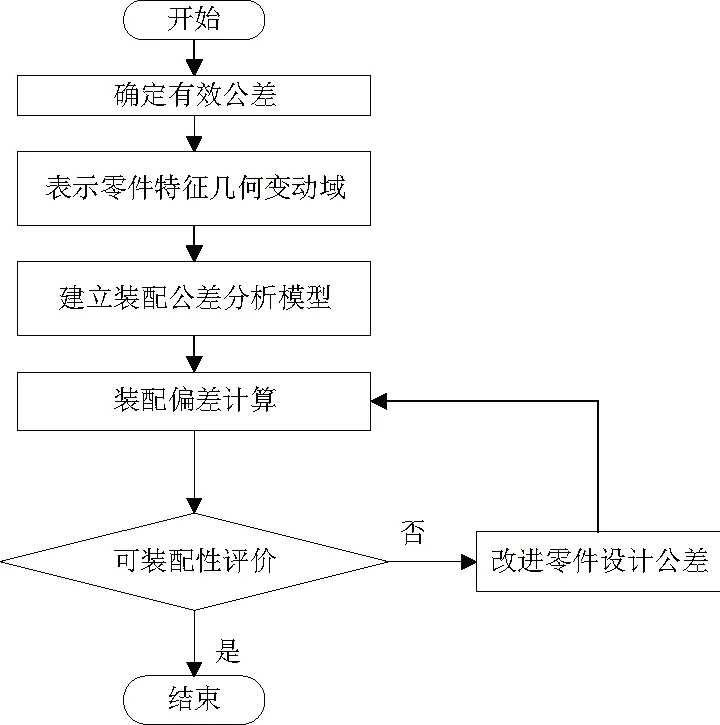
图2 可装配性分析流程图
2 重载转动副的装配公差模型
2.1 基于精度目标的有效公差
零件本身包含的尺寸偏差、几何偏差及相互配合的零件特征之间的偏差会对零件装配过程偏差产生影响。零件具有的上述偏差与其公差存在相对应的关系,因而在研究装配过程产生偏差之前需要对零件公差和零件之间的配合公差进行分析。因为在装配过程中零件的偏差并不都是随着组装的进行而传递和累积,这就需要根据装配过程的精度目标确定零件的有效及无效公差。因此,确定零件能在装配过程中传递与累积的装配偏差所对应的公差为有效公差。
2.2 基于坐标转换矩阵的装配公差分析模型
基于刚体和微小变动量假设,将零件特征或要素的几何变动量用SDT(smalldisplacementtorsor,小变量簇)表示。SDT是由沿x,y,z轴的3个平移自由度和3个旋转自由度相对应的微小偏移,以dx、dy、dz、δx、δy、δz来表示。用这6个分量的变动范围可以描述零件特征或要素相对于其应在位置或状态的几何变动域。
坐标转换矩阵在运动学中是用4×4矩阵来描述两个刚体的空间几何关系。基于几何变动在装配体中的传递方式,本文用坐标转换矩阵来表达零件间特征或要素间的几何关系。两个不同坐标系之间的平移和旋转关系可用转换矩阵T表示[5]:
T=Tn+dTn
(1)
其中:Tn表示公称转换矩阵;dTn表示微分转换矩阵。
当两个坐标系的X,Y和Z轴方向相同时,两个不同坐标系之间按照理想状态下零件的尺寸和零件间几何关系所决定的平移和旋转关系用公称转换矩阵Tn表示如下:
(2)
其中(Dx,Dy,Dz)是两个坐标系之间的平移向量。
实际装配过程中坐标系实际位置和方向因公差和间隙等因素带来的装配偏差而产生的微量影响用微分转换矩阵dTn表示如下[8]:
dTn=ΔTn
(3)
其中偏差传递矩阵
Δ=Trans(dx,dy,dz)Rot(x,δx)Rot(y,δy)Rot(z,δz)≈
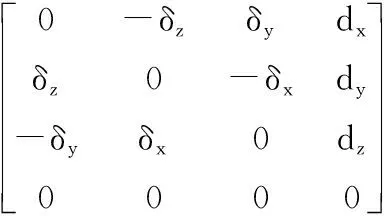
(4)
若有n个坐标系E1,E2,…,En,T12,T23,…,T(n-1)n为n个坐标系之间的坐标转换矩阵,任意S点在第n个坐标系中的坐标为Sn,那么S点在第一个坐标系中的坐标S1为:
S1=T12T23…T(n-1)nSn
(5)
3 考虑装配过程的重载转动副偏差计算模型
如图1所示,轴承内圈与轴是过盈配合,因此不考虑轴承内圈和轴径的尺寸公差及其配合公差,将轴和轴承当作一个整体考虑。根据先内后外、先重后轻、先主件后紧固件的经验原则,对重载转动副可能存在的装配序列进行规划,因此转动副装配序列存在的差别主要是轴系组件轴承1和轴承2的装配先后关系。现以轴承1优先装配的装配过程来评价转动副的可装配性。装配偏差传递路径为:底座—轴承1—轴—轴承2。
由于重载转动副的配合方式主要考虑轴孔配合,定义孔的直径为D±ΔD,轴的直径为d±Δd,孔和轴的直径均设服从正态分布,因此,轴孔之间的间隙也服从正态分布。根据“3σ原则”,间隙带在此区间内服从正态分布,其宽度最可能出现的区间为:
(6)
轴承外圈与底座内孔的配合为间隙配合,其轴孔配合间隙类型如图3所示。装配的定位面为零件1的圆柱表面。间隙带的宽度C最可能出现的区间可根据式(6)得到,且宽度C在此区间内服从正态分布,和有效公差一样,间隙带也可以转化成装配偏差,从而在装配过程中不断传递和累积。对于此类轴孔间隙配合,以零件2为基准,由间隙带引起的零件1的装配偏差为:
(7)

图3 轴孔配合间隙
重载转动副零件配合方式大多是轴孔配合,因此装配过程的偏差累积主要是在Y方向上的偏差。根据图4(a)所示的底座与图4(b)轴系组件的主要零件及有效公差符号表示,重载转动副装配过程的精度分析主要是根据已给定的装配顺序研究先装配的零件轴承1装配后的中心点O1和轴承2装配后的中心点O2在Y方向的偏差大小。通过比较配合特征底座内孔2与轴承2外圈装配产生的间隙,判断此装配过程重载转动副的可装配性。特引入坐标转换矩阵的方法,根据此方法计算得到O1和O2的坐标,由此得到两点在Y方向的距离,此距离就是偏差值。

图4 主要零件尺寸及有效公差符号表示
在进行重载转动副偏差计算之前,需要根据精度分析目标及装配过程确定装配公差的分析路径,对于重载转动副的装配,应建立如下2条装配公差分析路径:
路径1:O1→O1
路径2:O1→O2→O2
其中,O1、O2分别为底座内孔1和底座内孔2的中心,O1和O2分别为轴承1和轴承2装配后的中心点(理论上O1应与O1重合,O2应与O2重合)。
根据重载转动副装配过程,按照设定的2条路径,可计算出相应的坐标转换矩阵。
a) 路径1
轴承1外圈与底座内孔1属于如图3所示轴孔配合方式,根据式(1)可得O1→O1的坐标转换矩阵T11:
T11'=
[-C1/H1,C1/H1] 表示的是区间范围。根据式(6),在此考虑宽度C1出现的最坏情况,取
O1在绝对坐标系中的坐标:
b) 路径2
1) 计算O1→O2坐标转换矩阵T12
由于底座两内孔之间存在同轴度,定义其沿X、Y轴方向的平动分别为Δu和Δυ,则:
满足条件:
(8)
2) 计算O2→O2坐标转换矩阵T22
轴承2外圈与底座内孔2属于如图3所示轴孔配合方式。
T22'=
宽度C2的取值与宽度C1的取值同理可得。由式(5)及以上1),2)两步可得O2在绝对坐标系中的坐标
O1和O2在绝对坐标系中的最小距离为:
(9)
O1和O2在绝对坐标系中的最大距离为:

(10)
底座内孔2与轴承2外圈装配间隙P范围为:
[D2-ΔD2-d2-Δd2,D2+ΔD2-d2+Δd2]
(11)
4 考虑装配精度的重载转动副可装配性分析
在完成了相应坐标的求解之后,一般能够得到精度分析目标在绝对坐标系下的位置及尺寸范围。定义重载转动副可装配性为:在满足精度分析目标的情况下,考虑装配过程中由零件公差和间隙引起的装配偏差的累积能否由零件配合特征产生的间隙进行抵消。此时会出现多种可能性,若装配累积偏差的范围与零件配合特征产生的间隙范围存在交集,则称重载转动副存在可装配性,但不一定能装配成功;若装配累积偏差的最大值都小于零件配合特征产生的间隙最小值,则可以确保重载转动副能装配成功;若装配累积偏差的最小值都大于零件配合特征产生的间隙最大值,则称重载转动副不具有可装配性。
根据重载转动副偏差计算过程,对重载转动副的可装配性评价进行参数化定义。根据式(9)、式(10),间隙带的宽度分别取极值的情况下,重载转动副的偏差值区间为:
(12)
基于上述装配过程的重载转动副存在可装配性时满足条件:
(13)
此时,重载转动副存在可装配性,但不一定能装配成功,因此确保重载转动副能装配成功应满足条件:
(14)
同时,当重载转动副不具有可装配性时满足条件:
(15)
采用轴承2先装配的装配过程,重载转动副可装配性评价同理可得。通过可装配性条件分析,便能得到基于可装配性评价不同装配过程的优劣。上述评价方法将重载转动副装配过程与可装配性综合考虑进行研究。
5 应用实例
图5所示为某型雷达天线举升机构重载转动副装配示意图,采用的轴承型号为30210,选用的精度等级为0级。底座内孔同轴度及中心距如图4,分别为0.025mm及152±0.1mm。
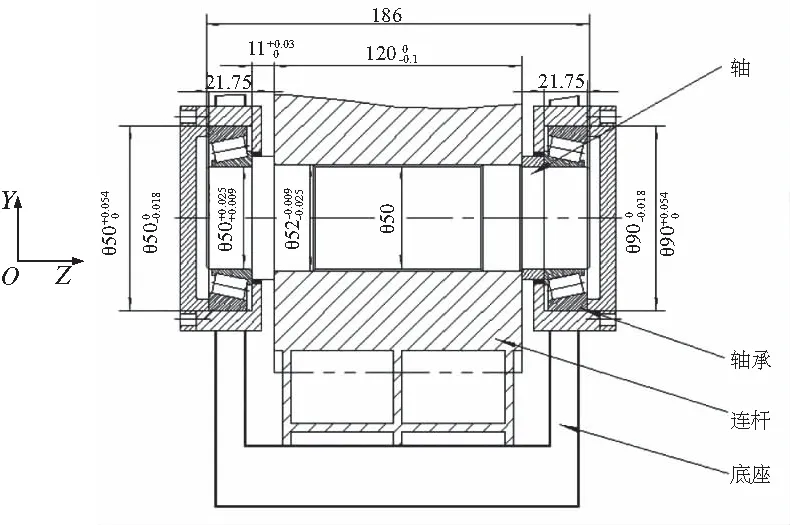
图5 转动副装配示意图
根据轴孔配合方式,重载转动副在径向的装配偏差累积会对其装配精度造成较大的影响,因此确定有效公差时主要考虑零件在径向可累积偏差对应的公差。针对重载转动副装配实例及装配精度目标,确定其各有效公差如表1所示。根据文献[5] ,为方便计算,特将图5中公差表示形式等效于表1中公差表示形式。
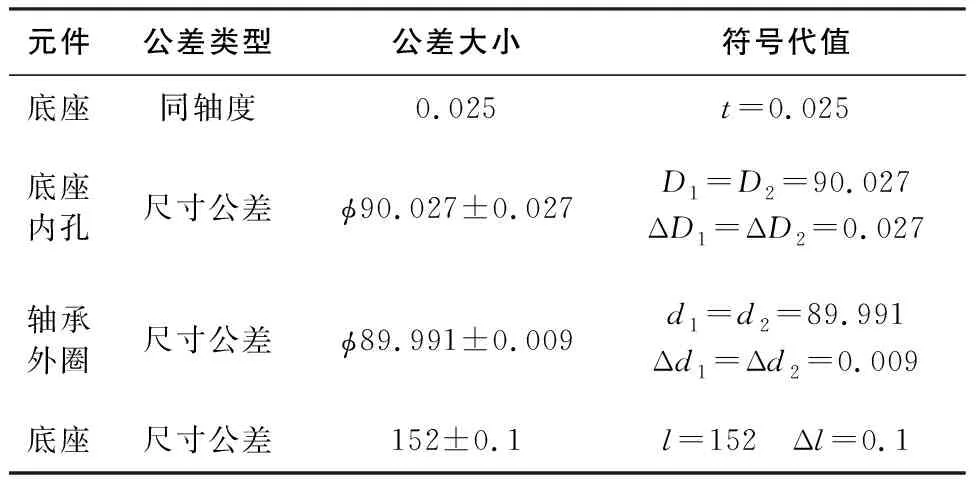
表1 重载转动副中各有效公差表示 mm
且H1=H2=21.75mm。
根据轴承1优先装配的装配过程,O1和O2在绝对坐标系中的最小距离根据式(9)计算为∣Δv∣,O1和O2在绝对坐标系中的最大距离根据式(10)计算为(0.064 5+∣Δv∣)mm,而底座内孔2与轴承2外圈装配间隙P范围可根据式(11)计算为[0,0.072]mm。
针对重载转动副实例,其可装配性主要考虑装配过程产生的偏差累积能否由后装配的轴承外圈与底座内孔装配产生的间隙抵消。而根据式(8),同轴度t=0.025mm,可得∣Δv∣≤0.012 5mm,通过式(13)、式(14)分析可得结果满足重载转动副存在可装配性的条件,但不一定能装配成功。由于此类重载转动副考虑装配过程偏差累积时的有效公差左右两边是对称分布,且具体数值相同,因此考虑轴承1先装配或者轴承2先装配结果相同。
6 结语
1) 本文以雷达天线举升机构中重载转动副为对象,从装配精度着手研究其可装配性。首先根据重载转动副的精度目标确定了零件的有效公差,然后基于公差分析路径和坐标转换矩阵的方法得到了基于装配过程的累积偏差,最后与零件配合特征产生的间隙进行比较。由此提出了重载转动副可装配性的概念,同时针对装配过程进行了参数化定义,并通过实例进行说明。
2) 本文所提出的重载转动副可装配性评价方法可以有效地指导雷达天线举升机构中重载转动副的装配规划,避免由于设计偏差及装配顺序不合理而导致的不可装配性,提高了整机的装配成功率。并且该可装配性分析过程不仅只适用于此类转动副也同样适用于间隙配合的装配体,具有一定的工程应用价值。
