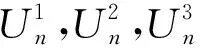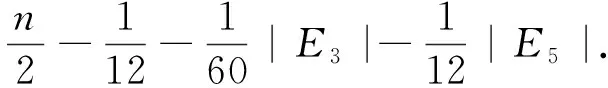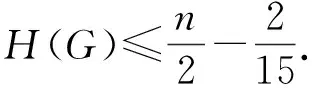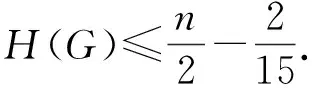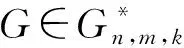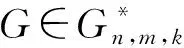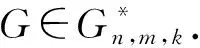具有k个悬挂点的化学图的调和指数

孙晓玲, 高玉斌, 杜建伟

(1. 中北大学 仪器与电子学院, 山西 太原 030051; 2. 中北大学 理学院, 山西 太原 030051)

0 引 言

式中：d(u)表示G中顶点u的度. 调和指数对于预测化合物的物理化学性质(如沸点、 生成焓、 色谱保留时间、 Antoine方程(蒸汽压)中参数、 表面积和水中溶解度等)有着积极的意义.

本文所考虑的图G=(V(G),E(G))均为简单连通图, 其中V(G)是G的顶点集,E(G)是G的边集.NG(u)(简写为N(u))表示G中顶点u的所有邻点构成的集合，dG(u)=|NG(u)|(简写为d(u))表示G中顶点u的度. 如果d(u)=1， 则称点u为悬挂点. 一条边的一个端点为悬挂点， 称该边为悬挂边. 设Ps=v0v1…vs是G中的一条路, 满足d(v1)=d(v2)=…=d(vs-1)=2(除非s=1). 如果d(v0)=1且d(vs)≥3, 则称Ps是G中的一条悬挂链. 如果一个连通图G的最大度不超过4, 则称该连通图为分子图或化学图. 一个(n,m,k)-图是指具有n个顶点,m条边和k个悬挂点的连通图. 显然, (n,n-1,k)-图是树, (n,n,k)-图是单圈图, (n,n+1,k)-图是双圈图, (n,n+2,k)-图是三圈图.

设G=(V(G),E(G))是一个简单连通图. 为了方便讨论， 还定义了以下记号

Vi(G)={u|u∈V(G),d(u)=i},

ni=|Vi(G)|,

E1={uv∈E(G)|d(u)=1,d(v)=2},

E2={uv∈E(G)|d(u)=d(v)=2},

E3={uv∈E(G)|d(u)=2,d(v)≥3},

E4={uv∈E(G)|d(u),d(v)≥3},

E5={uv∈E(G)|d(u)=1,d(v)≥3}.

文中未加说明的术语和记号可参看文献[17].

引理1[3]设G是n阶连通图, 则

等号成立当且仅当G是正则图.

引理2[18]设G是n阶连通图， 则

设G是(n,m,k)-图, 易知m≥n-1且k≥0. 如果k=0, 由引理1可知, 具有最大调和指数的化学(n,m,0)-图是r-正则图, 其中r=2,3,4. 另外, 具有最大调和指数的化学(n,n-1,k)-图在文献[19]中已被刘少强和李建喜所确定， 所以下面只讨论k>0且m≥n的情况. 用Gn,m,k表示满足k>0且m≥n的(n,m,k)-图的集合.

引理3 设

则对于x>2， 有f(x)<0.

证明对于x≥2, 有

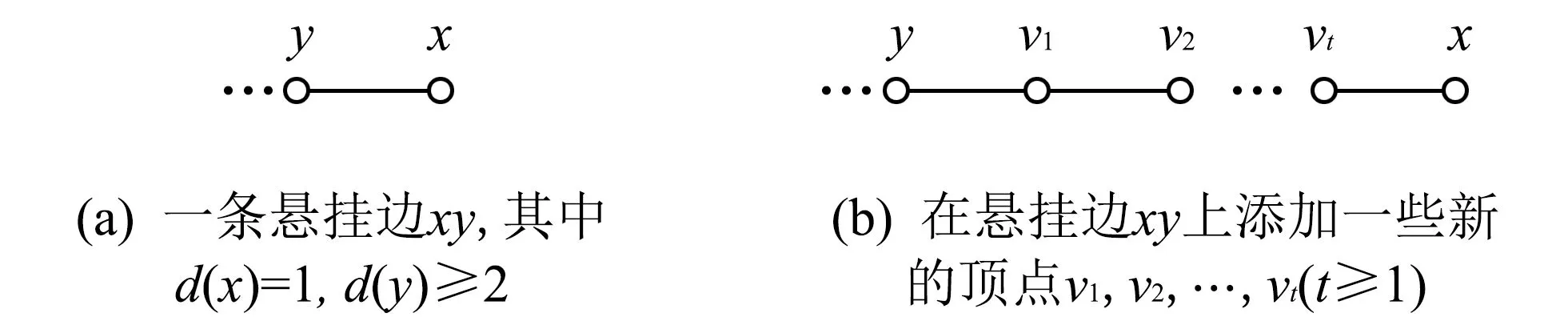
故f(x)在x∈[2,+∞)上严格单调递减. 于是对于x>2, 有f(x)

引理4 设

其中x,y>2, 则g(x,y)<0.

证明对于固定的y>2, 有

所以g(x,y)关于x严格单调递减. 又由于g(x,y)关于x,y对称, 所以对于固定的x>2,g(x,y)关于y也严格单调递减. 此外,g(x,y)是关于x,y≥2的连续函数, 因此， 对x,y>2, 有g(x,y)

引理5 设

则h1(x)在x∈[3,+∞)上单调递增.

所以h1(x)在x∈[3+∞)上单调递增.

与引理5证明类似， 可以得到下面的引理6.

引理6 设

则h2(x)在x∈[3,+∞)上单调递增.

引理7 设G∈Gn,m,k. 假定u∈V(G)是一个2度点, 且该点既不在任何一个悬挂链上也不在任何一个3圈中. 设点u的邻点度至少为2, 则存在图G′∈Gn,m,k, 使得以下情形之一成立：

1)H(G)

2)H(G)=H(G′)且G′中悬挂链的顶点数比G中悬挂链的顶点数多.

证明记NG(u)={v,w} (其中dG(u)=2),dG(v)=p≥2,dG(w)=q≥2.设x是G中的一个悬挂点,y是其邻点， 则dG(y)=l≥2. 令G′=G-uv-uw-xy+vw+xu+yu, 易知G′∈Gn,m,k, 另外, 有

如果l>2或p,q>2, 由引理3和4, 可得H(G)

图 1 在悬挂边上添加新顶点的操作Fig.1 The operation of adding new vertices on pendant edge

1 主要结论

定理1 设G∈Gn,m,1满足m=n或m=n+1， 则

(1)

图 2 四个具有最大调和指数的(n,m,k)-图Fig.2 Four extremal-graphs with maximum harmonic index

证明设G∈Gn,m,1满足m=n或m=n+1， 则E(G)=E1∪E2∪E3∪E4∪E5， |E1|+|E5|=1. 由引理2， 5和6， 有

H(G)=

现在考虑下面两种情况.

情况1m=n(n≥5)，G是单圈图.

情况2m=n+1(n≥6)，G是双圈图.

现假定(1)中等号成立， 那么以上所讨论的不等式必须都取等号. 因此， 有i)|E1|=1， |E5|=0； ii) 对于任意的uv∈E3， 有d(u)=2,d(v)=3及|E3|=3； iii)对于任意的uv∈E4， 有d(u)=d(v). 由于E3的每条边都分别与E4的一条边相邻， 与一个2度点关联， 所以对于任意的uv∈E4， 有d(u)=d(v)=3， 这表明G∈Bn. 反之， 容易验证(1)中的等号对于Bn是成立的. 证毕.

与定理1证明类似， 可以得到下面的定理2.

定理2 设G∈Gn,n,2， 则

定理3 设G∈Gn,m,k满足m=n且k≥3， 或m=n+1且k≥2， 或m≥n+2， 则

(3)

H(G)=

在实际中， 有许多烃类化合物的分子图是(n,m,k)-图， 如脂环烃、 芳香烃等.它们的物理化学性质(如沸点、 熔点、 生成焓等)与调和指数间往往存在着线性关系， 以熔点为例， 熔点越高， 调和指数越大.因此， (n,m,k)-图的调和指数的极值问题是一个值得研究的课题， 运用本文所得结论可以帮助我们更好地分析和预测烃类化合物的物化性质.