考虑能耗的自动化码头装卸设备协调调度

艾立红，韩晓龙

(上海海事大学物流科学与工程研究院，上海 201306)

0 引 言

作为航运与陆运交通的枢纽站，集装箱码头在全球供应链中发挥着重要作用。随着物流量的增长和人力成本的上升，自动化码头越来越受到青睐，其采用的自动化装卸设备能进一步提升码头装卸效率，降低运输成本，对提高经济效益和社会效益具有重要意义。自动化集装箱码头的装卸设备主要有3种，即岸桥(quay crane，QC)、自动引导车(automated guided vehicle，AGV)和自动堆垛机(automated stacker crane，ASC)，三者的作业效率和合理调度是自动化码头装卸效率和节能效益提升的关键。

当前，环境污染和能源消耗已经受到广泛关注。集装箱码头由于拥有相当数量的大型装卸设备，是环境污染的源头之一。绿色港口是未来港口建设的重要方向，其要求在尽量提高码头服务水平的情况下，减少能源消耗和碳排放。

关于集装箱码头装卸设备调度方面的研究较多。韩晓龙等[1]针对卸船作业，考虑集卡到达时间的不确定性，以最小化集卡完工时间为目标函数，建立了QC与集卡协同调度模型，并用改进的遗传算法求解。CAO等[2]针对作业于进口集装箱的QC和集卡调度，建立混合整数规划模型，并综合利用遗传算法和基于约翰逊规则的启发式算法求解，提高了求解精度。LAU等[3]考虑QC在作业过程中的最佳作业顺序，以最小化QC操作延迟时间、AGV总行程时间和自动化场桥(automated yard crane，AYC)总行程时间为目标，建立了混合整数规划模型，并用多层遗传算法和遗传最大匹配算法求解。乐美龙等[4]以船舶在港停靠时间最短为目标，建立了自动化码头QC、AGV和AYC的联合调度模型，并通过算例验证了模型的有效性，该模型可以提高码头运输效率。LU等[5]考虑了内集卡行驶速度，场桥水平运行速度、装卸速度等不确定性因素，以最小化QC、集卡和场桥的操作总时间为目标建立模型，用粒子群优化算法求解。KAVESHGAR等[6]考虑了集装箱任务之间的优先关系、QC之间的干扰和码头安全裕度等现实约束，建立了QC和集卡的协调调度，并结合遗传算法和贪婪算法进行了求解。添玉等[7]针对自动化码头自带提升功能的AGV和起重机的集成调度，考虑设备间的相互制约，建立了多目标混合整数规划模型，并用双层遗传算法求解。罗勋杰[8]基于目前全球全自动化码头水平运输系统的应用现状，对AGV和自动跨运车两种主要运输方式进行了对比分析。卢毅勤[9]考虑内集卡和场桥作业过程中的不确定性因素，构建了堆场设备集成调度优化模型，以探讨不确定因素对堆场设备作业的影响。杨勇生等[10]考虑AGV和轨道式龙门吊(rail-mounted gantry crane，RMG)的任务分配约束，构建AGV和RMG的协同调度模型，得出AGV、QC和箱区数量不同时的卸船完工时间。严庭玉[11]根据集装箱码头装卸作业特点和运作方式，基于图论方法构建了装卸设备的网络调度模型，将该模型的结果与集成调度模型的结果进行对比，证明了所建模型的有效性。

考虑能耗的集装箱码头设备调度的文献较少。HE等[12]以最小化所有船舶的总离港延迟时间和所有任务的总能耗为目标建立混合整数规划模型，开发了一种基于仿真的优化算法求解。严南南等[13]考虑了集卡能耗，建立QC与集卡协调调度的双目标模型，并用遗传算法求解。郭婵婵[14]基于混合流水车间的思想，以作业时间最短和作业能耗最低为目标，建立QC、集卡和场桥调度的多目标模型。SHA等[15]在考虑起重机移动距离、转弯距离以及与总能耗直接相关的、基于实际运行规律的关键因素的基础上，建立了集装箱码头堆场起重机的调度模型，以减少起重机的总能耗。

相比已有文献，本文在集装箱自动化码头QC、AGV和ASC的协调调度问题中考虑了装卸设备的能耗约束。已有的关于集装箱码头设备调度的文献，大多只考虑一种设备或两种设备的协调调度，而对能耗的考虑多体现在宏观层面(如建立绿色港口评价指标体系等)，在运营层面考虑得较少，只有较少文献考虑了集卡的能耗。本文以定量方法将能耗考虑到自动化码头装卸设备的协调调度中，以设备总作业时间最短和能耗最低为目标，建立包括QC、AGV和ASC的双目标调度模型。

1 模型构建

1.1 问题描述

考虑多QC、多AGV和多ASC的情况，集装箱作业过程为：在卸船过程中，船上集装箱被根据贝位分配给不同的QC，每台QC将集装箱卸载到AGV上，AGV将集装箱运到指定的堆场箱区，每个箱区配备1台ASC将集装箱卸载到对应箱区。装船过程与之相反。本文要实现两个目标，分别为QC、AGV和ASC这3种设备总作业时间最短和总能耗最低。

模型假设：(1)不考虑AGV的路径优化；(2)ASC不能跨箱区作业；(3)ASC在计划期内只服务于内部AGV。

1.2 符号定义

参数：Q为QC集合,q∈Q；K为AGV集合，k∈K；R为ASC集合,r∈R；J为所有集装箱作业任务集合,j∈J(|J|=n)；Jq为QCq的作业任务集合，q∈Q，Jq⊂J(|Jq|=nq)；Jr为ASCr的作业任务集合，r∈R,Jr⊂J(|Jr|=nr)；αt为AGV空载时单位时间的行驶能耗，unit/s；αw为AGV负载时单位时间的行驶能耗，unit/s；αv为AGV单位时间的等待能耗，unit/s；γ为QC 单位时间的平均能耗，unit/s；η为ASC单位时间的平均能耗，unit/s；tkj为AGVk从任务j的起点行进到任务j终点的时间；tkjj′为AGVk从上一任务j的终点行进到当前任务j′起点的时间；trjj′为当任务j与j′在同一箱区时，ASCr从堆场任务j终点行进到任务j′起点的时间；tqjj′为任务j和j′由同一台QCq作业时，QCq从任务j终点行进到任务j′起点的时间；τ为QC装卸单位集装箱的时间；p为ASC装卸单位集装箱的时间；λj∈{0,1}，若j为出口箱则λj为1，否则为0。

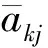
1.3 能耗模型构建

(1)

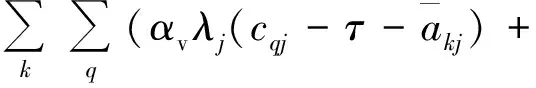
(2)

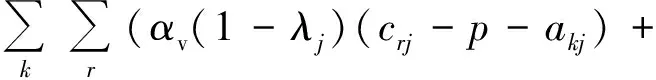
αvλj(crj-akj))

(3)

(4)

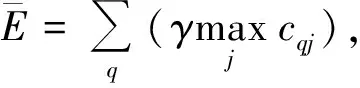
(5)

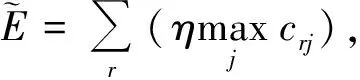
(6)

除有特殊说明外，上述模型中：q∈Q;k∈K;r∈R;j,j′∈J,j≠j′。式(1)为AGV从任务j终点行进到下一任务j′起点的能耗；式(2)为AGV等待QC完成任务j的能耗；式(3)为AGV等待ASC完成任务j的能耗；式(4)为AGV将任务j从起点运到终点的能耗；式(5)和(6)分别为QC和ASC在整个工作时间内的能耗。

1.4 数学模型

(7)

(8)

(9)

(10)

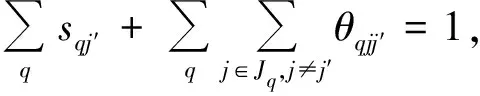
(11)

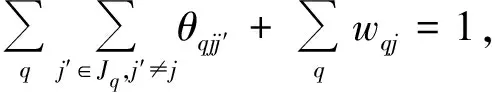
(12)

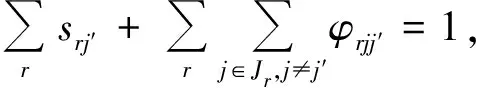
(13)

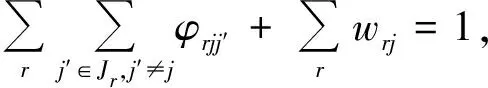
(14)

(15)

(16)

(17)

ckj≥(1-λj)(crj-p), ∀j∈Jr

(18)

ckj≥λj(cqj-τ), ∀j∈Jq

(19)

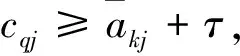
(20)

crj≥akj+p, ∀j∈Jr

(21)

akj′+M(1-φkjj′)≥(ckj+tkjj′φkjj′)λj′

(22)

(23)

akj≥(cqj+tkj)(1-λj), ∀j∈Jq

(24)

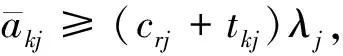
(25)

crj′-p+M(1-φrjj′)≥crj+trjj′,

∀j,j′∈Jr,(j≠j′)

(26)

cqj′-τ+M(1-θqjj′)≥cqj+tqjj′,

∀j,j′∈Jq,(j≠j′)

(27)

skj′,wkj,srj′,wrj,sqj′,wqj,θqjj′,φkjj′,φrjj′,

λj∈{0,1}

(28)

(29)

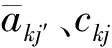
2 遗传算法

遗传算法是一种模拟生物自然进化过程的启发式搜索算法。由于遗传算法具有全局搜索的特征，并且搜索速度较快，所以用遗传算法求得的解通常比用其他方法得到的解更优。遗传算法的编码方法简单，搜索面广，交叉、变异等遗传操作也较易实现，已被广泛应用于组合优化、生产调度、信号处理、自适应控制和人工生命等领域。

本文先用遗传算法求解能耗值；根据求得的结果，设置不同的能耗值作为约束条件；对满足能耗约束条件的染色体求适度应值，对不满足能耗约束条件的个体(劣质个体)设其适应度值为0，继续进行遗传算法求解(如图1)，实现能耗对求解最短时间目标的约束功能。能耗约束值是可以调节的。

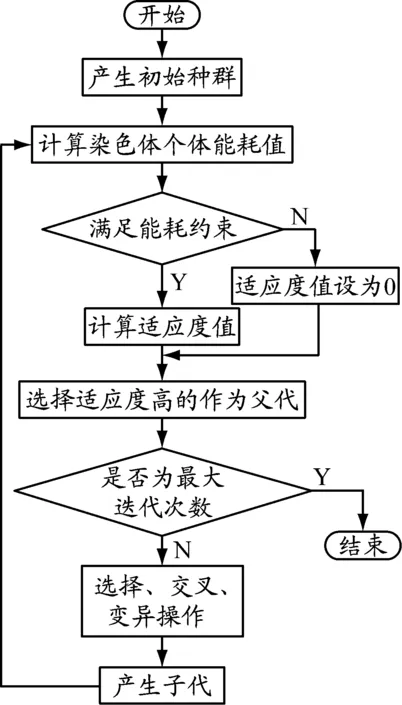
图1 遗传算法流程

2.1 染色体编码

每台QC和ASC需要作业的集装箱编号是已计划好的，因此对每台QC和ASC只需要优化其作业序列。本文针对QC、AGV、ASC的协调调度问题，采用双层实数编码方式。如图2所示，每个染色体有2行：第一行代表集装箱编号，编号序列即为相应集装箱被作业的顺序；第二行代表为相应集装箱分配的AGV编号。设有10个集装箱，按照计划，集装箱1～5由QC1完成，集装箱6～10由QC2完成，集装箱1、2、3、9、10在堆场箱区1由ASC1作业完成，集装箱4～8在堆场箱区2由ASC2完成。根据图2和集装箱分配计划，QC1作业顺序为3→5→1→4→2，QC2作业顺序为8→7→9→10→6，AGV1作业顺序为8→2，AGV2作业顺序为7→4，AGV3作业顺序为3→1→6，AGV4作业顺序为5→9→10，ASC1作业顺序为3→1→9→10→2，ASC2作业顺序为5→8→7→4→6。

图2染色体编码

2.2 种群初始化

随机产生初始化种群，见图3。在初始种群中，集装箱编号的序列随机生成，并且随机分配AGV作业于不同的集装箱。

2.3 适应度函数

对满足能耗约束条件的染色体个体计算适应度值。本文的目标是求取最小值，因此取目标函数的倒数作为适应度函数，即适应度函数F(x)=1/f1。目标函数值越小，适应度值越大，相应染色体被保留下来的概率就越大。

图3随机生成染色体个体

2.4 选择、交叉、变异操作

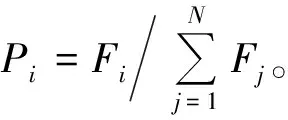
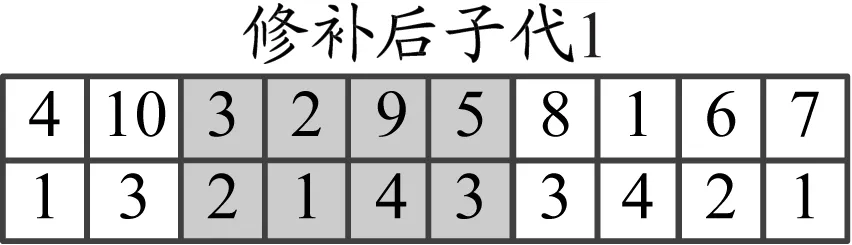
为提高收敛速度，采用两点交叉的方式。随机选择2个染色体和2个基因位，2个基因位的中间部分作为交叉部分。交叉完成后，子代个体中集装箱编号有重复、缺失现象(见图4)，因此要对子代染色体进行修补，将重复集装箱编号剔除，补充为缺失的集装箱编号(见图5)。

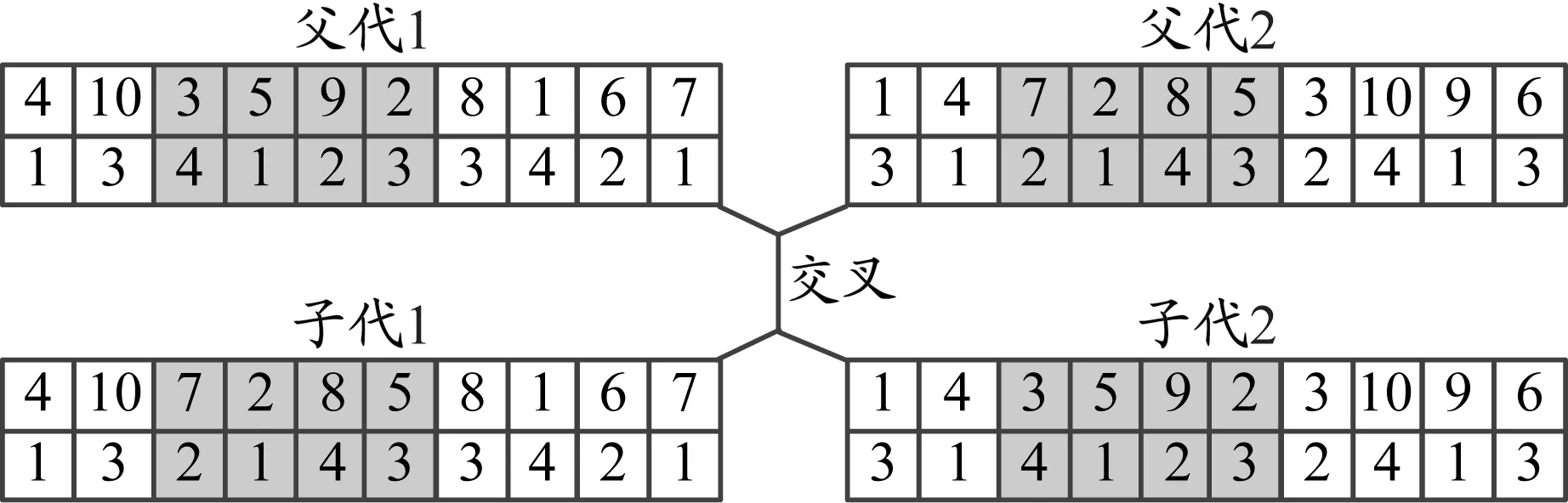
图4 染色体个体交叉

随机选择一个染色体上的基因位，根据变异因子决定是否变异。变异时，如果对编码的第一行进行变异，则变异完成后需进行修补，修补的编码仍是变异前的编码，因此对编码的第一行进行变异是没有意义的，只需要对编码的第二行进行变异，见图6。

图6染色体个体变异

3 案例分析

3.1 初始数据设计

设有1艘船，2台QC，4辆AGV，2台ASC，50个集装箱。设备作业于集装箱时，根据查阅到的文献随机生成初始参数，其他恒定参数根据查阅到的文献设置，见表1。

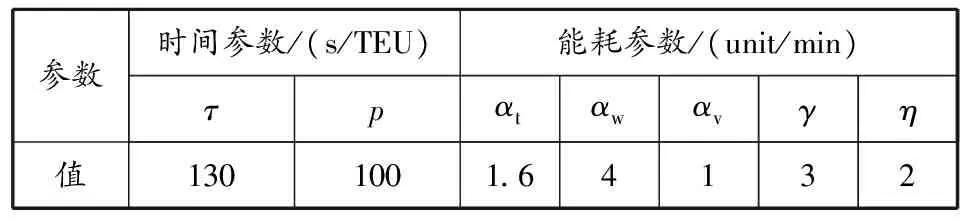
表1 参数设置

装卸设备的作业时间通常以s为单位，但为便于计算能耗，表1中能耗单位采用unit/min。QC和ASC在提起集装箱和平移过程中能耗是不同的，为方便计算，取QC和ASC在作业过程中的平均能耗分别为3 unit/min和 2 unit/min。

3.2 案例结果

设置最大迭代次数为500，种群规模为100，交叉概率为0.6，变异概率为0.01。

先计算得到装卸设备的总能耗为1 600～5 000 unit。若能耗约束值过低，则装卸时间会很长，不符合码头高效率的实际工作要求；若能耗约束值过高，则达不到节约能耗的要求。因此，分别设置能耗约束值为3 400、3 200、3 000、2 800、2 600 unit，计算装卸设备在不同能耗约束下的作业时间和作业能耗，结果见表2。

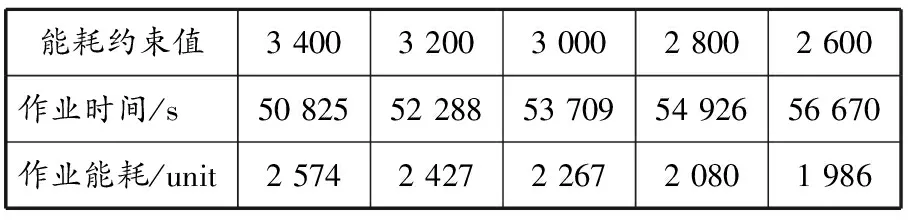
表2 不同能耗约束下的作业时间和作业能耗

当不考虑能耗时，直接计算使作业时间最短的目标函数，算法在迭代次数为70时收敛(图7a)，此时最短作业时间、作业能耗分别为48 378 s和2 728 unit；当能耗约束值为3 400 unit时，算法在迭代次数为110时收敛(图7b)，此时最优解(即最短作业时间)比不考虑能耗时的最优解多2 447 s(约40.8 min)，但节省能耗154 unit。

由表2可知，能耗约束值越低，装卸设备作业能耗就越低，但相应的作业时间就越长。当能耗约束值为2 600 unit时，装卸设备作业能耗降至1 986unit，比不考虑能耗时节省742 unit，但装卸设备的最短作业时间比不考虑能耗时的最短作业时间多8 292 s(138.2 min)，装卸效率大大降低。这可能是因为在装卸过程中，为追求低能耗：AGV可能会延长等待时间，从而缩短了空载行驶时间和负载行驶时间；QC、AGV和ASC可能会改变集装箱的作业顺序，从而降低设备作业能耗，延长了装卸设备总的装卸时间。

表2中的结果是在满足不同能耗约束值的条件下求得的最短作业时间和最低作业能耗，结果处于front解集，是解集中的一部分解。从表2可以看出，在计算结果中，没有一个使作业时间和作业能耗同时最小的解，码头运营商可根据需要选择相应的调度方案。如果运营商对节能要求较高，则设置较低的能耗约束值；如果运营商需要更高的效率，则设置较高的能耗约束值。

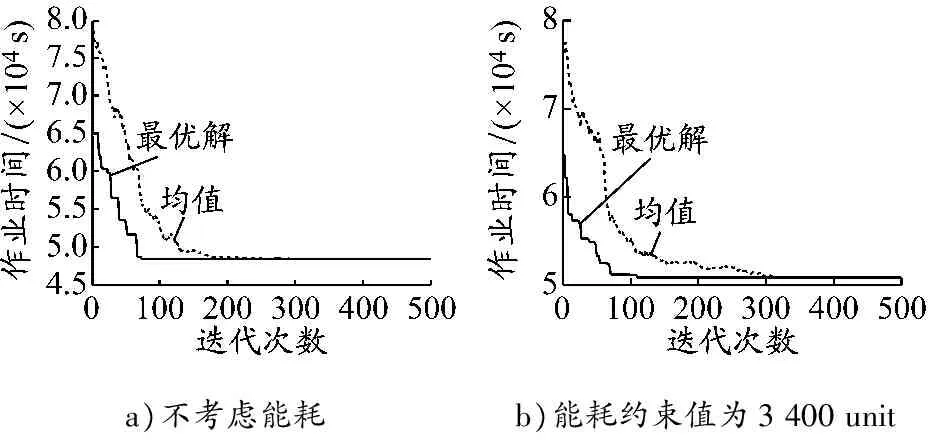
a)不考虑能耗b)能耗约束值为3 400 unit

图7作业时间收敛曲线

4 结 论

与以往文献相比，本文将能耗量化，构建了考虑能耗的自动化码头装卸设备协调调度的双目标模型，并用遗传算法求解。结果显示，自动化码头装卸设备在进行集装箱装卸时，考虑能耗比不考虑能耗消耗的时间更多，但能耗更少，而且能耗要求越低，装卸时间就越长。本文针对自动化码头低耗能和高效率目标，研究码头装卸设备协调调度问题，符合绿色码头的建设要求和未来港口的发展趋势。本文在构建模型时，没有考虑AGV的路径优化，而AGV的行驶路径对码头装卸效率和能耗有同样重要的影响，因此以后的研究方向是将AGV的行驶路径考虑到装卸设备的协调调度中，对码头设备装卸效率与能耗进行更好的权衡。