基于测试信息熵的控制系统最优故障诊断路径规划方法
2019-01-07刘清竹
周 虎 卢 波 刘清竹
1.北京航天自动控制研究所,北京100854 2.宇航智能控制技术重点实验室, 北京100854
导弹武器控制系统通常通过采用高性能软硬件产品、设计合理的冗余与容错方案等手段来保障系统整体可靠性。但作为一项复杂的系统工程,受元器件性能、环境条件以及其他未识别因素的影响,客观上导弹武器控制系统依然会不可避免地出现工作异常的情况,影响装备实战化能力。因此,必须对导弹武器控制系统工作状态进行测试监控,并及时响应和处理工作过程中可能出现的各类异常现象,即控制系统的故障诊断技术。
控制系统故障诊断技术特别是快速故障诊断能够通过合理的测试流程,迅速获得系统完整、准确的状态信息,及时给出系统状态良好、发射准备就绪的结论;当系统存在隐患时,能够实现对故障的快速定位,因而对于导弹武器控制系统有着十分明显的意义:在导弹武器发射准备阶段,基于故障诊断技术能够将控制系统故障快速定位于现场可更换单元,通过现场对故障产品进行及时更换或者维修处置,保证导弹武器发射可靠性,缩短发射准备时间[1],客观上提高了导弹武器射前的生存能力;在真实飞行阶段,通过故障诊断技术快速识别并定位故障,能够在有限的处置时间内利用系统冗余设计、重构软硬件等技术方案实施故障屏蔽,保障导弹武器飞行可靠并命中目标。
与之不相适应的是,尽管导弹武器控制系统测试覆盖性通常可以满足预定技术指标,但控制系统规模庞大,功能复杂,测试与故障定位仅基于预设串行固定流程,缺乏故障诊断流程优化理论指导,导致测试与排查故障的过程比较缓慢,耗费了大量人力物力资源和时间成本,难以满足系统测试发射控制时间约束和对维修性、保障性的要求[2]。
针对上述问题,提出的基于测试信息熵的最优故障诊断路径规划方法能够在对导弹武器控制系统进行测试性分析的基础上,有效利用控制系统历史故障统计数据和测试先验信息,动态计算故障诊断最短测试路径,大幅度提升控制系统故障隔离效率。
1 控制系统测试性分析
1.1 测试性建模原理
对控制系统进行全面的FMEA分析是测试性建模的前提和基础。其目的在于通过跟踪故障传播关系,评估其对系统性能的影响。若以有向图方式定义故障在设备间的传播路径,并增加对故障与系统测试间依赖关系的描述,即构成基于多信号模型[3]的测试性建模方法。
如图1所示,多信号模型包含3类基本元素:模块节点、测试节点和有向边。其中模块节点S1~S5是对一系列具备特定功能的硬件集合的抽象,模块节点可能包含一个或者多个具体故障。测试节点TP1~TP5是系统对硬件集合实施测试的物理或者逻辑位置,一个测试节点包括一个或者多个具体测试。有向边则反映了故障在不同模块节点间的传播关系,以及特定测试节点的测试覆盖范围。为充分描述硬件集合底层故障模式与传递路径,任一组硬件集合本身还可以表达为若干子模块节点、子测试节点以及有向边的组合,即所谓的分层建模方式[4]。

图1 基于多信号的测试性模型示意图
1.2 测试性模型的矩阵表示法
为讨论方便,设图1中模块节点S1~S5分别只包含一个可能的故障,测试节点TP1~TP5分别也只包含一项具体测试,并令对应的故障集、测试集分别为F={f1,f2,f3,f4,f5},T={t1,t2,t3,t4,t5}。通过分析控制系统设计原理图,易获得特定测试可直接覆盖的模块节点故障集合,如t4能够直接测试故障f2和f5是否发生,但不能确认故障f1,f3和f4的发生情况;而可能故障f1则可由t2和t5直接进行测试确认,但不能由测试t1,t3和t4确认。将故障集F与测试集T的这类相关关系表达为依赖矩阵形式D0=[dij]m×n,i=1…m,j=1…n,m和n分别为故障与测试数量。其中:
(1)
由上式可得图1对应的依赖矩阵满足:
(2)
根据FMEA分析结论,除影响自身所在模块节点功能外,故障还可能扩散至与之相邻的其他模块节点。同理,测试结果也间接反映了与之存在有向边连接关系而非就近布置的其他模块节点故障情况。因此,为完整地表达故障与测试间的依赖关系,还需要考虑故障与测试间的这种间接相关情况。
根据有向图建模结果,定义故障直接传播矩阵DA0=[alk]m×m,l,k=1,…,m,其中:
(3)
以及n维单位矩阵I,构造扩展矩阵K0:
(4)
基于图论原理[5],通过Warshall算法[6]求解扩展矩阵K0的传递闭包K:
(5)
则子矩阵D即为反映了直接与间接依赖关系的故障-测试全阶相关矩阵。式中,DA0和X分别为求解过程中相应的伴随矩阵。由式(2)~(6)可得图1对应的全阶相关矩阵D如式(6)所示,矩阵行与测试对应,列与故障对应。

(6)
式(6)为0-1二值矩阵,矩阵中测试对应行元素反映了该测试对于系统中各可能故障模式的覆盖情况,列值为1表示测试能够覆盖该列代表的测试,列值为0表示测试不能覆盖该列代表的测试。
2 故障诊断路径规划
2.1 扩展全阶相关矩阵
考虑到导弹武器高可靠性设计特性,控制系统通常在无故障模式下运行,为完整地描述系统工作状态,将无故障模式视为一类虚拟的故障状态,引入扩展全阶相关矩阵D*:
(7)
式中,矩阵D*中1行n列的向量0对应控制系统无故障运行状态与各测试间的相关关系。由于控制系统设置测试是基于检测某类故障模式的目的,因此可以抽象地认为,各测试均不能“检测”无故障状态,故向量0的各列元素均取0值。则测试tj能够检测覆盖的系统故障模式计数满足:
(8)
测试tj不能够检测覆盖的系统故障模式计数满足:
(9)
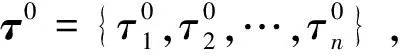
(10)
可使得各运行状态发生概率和为1。
2.2 测试信息熵
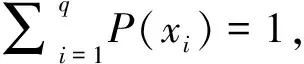
(11)
将任意测试视为信息源,则测试对应的事件即输出值仅包含2类:该测试能够检测覆盖的和不能检测覆盖的故障。虑及故障状态发生概率,测试对应的信息熵为:
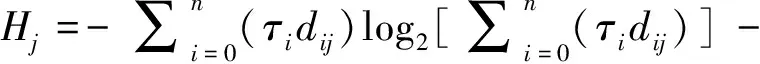
(12)

Hj=-xjlog2xj-(1-xj)log2(1-xj) (13)
控制系统应优先选择能够提供尽可能多信息的测试,即对于测试集T={t1,t2,…,tn},tj被首先用于故障诊断的条件为其对应的信息熵Hj理论上应满足以下约束条件:
Hj=max{H1,H2,…,Hn}
(14)
即有:
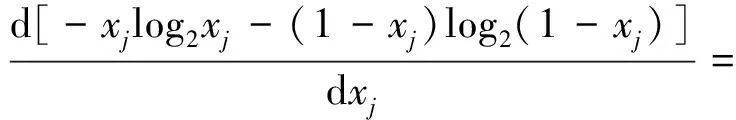
(15)
求解上式可得唯一极值点:
(16)
考虑到约束条件0 (17) 即Hj为定义域(0,1)内的凸函数,同时由式(13)可知,Hj为以xj=0.5为对称轴的对称函数。以上分析表明,若安排测试能够使得其能够检测和不能检测的故障模式发生概率尽可能相等,则该测试应为优先选择的测试项目。 首先对所有测试的信息熵进行评估,并将信息熵最大的测试作为首选测试项。根据该测试是否能够检测覆盖指定故障模式,将初始故障集分为2类子故障集。对子故障集继续应用测试信息熵评估方法,不断迭代优选,直至形成可用于故障定位的完整测试链。故障诊断测试路径规划具体执行过程如下所述: 1)定义控制系统扩展故障集F*={f0,f1,f2,…,fn},其中F={f1,f2,…,fn}为控制系统可能故障集,f0表示系统无故障状态。将F*作为待诊断的控制系统顶层可能运行状态集合Q; 2)以运行状态集合Q作为对象开展分析:枚举所有测试,对其测试信息熵Hj进行评估,搜索其中熵值最大的测试tk,即{tk|Hk=max(Hj)},并选择tk作为故障诊断顶层测试; 3)应用测试tk后,根据是否能够检测相应故障模式,原有运行状态集合Q被隔离为两类运行状态子集Q0与Q1。其中 (18) 令集合Q0与Q1中元素计数分别为m0和m1,则相应地,扩展全阶相关矩阵D*被分割为m0行n列和m1行n列的2个子矩阵D0与D1,其中m=m0+m1; 4)以运行状态子集Q0作为对象开展分析,判断m0值:若m0=1,表示控制系统故障被精确隔离;子集Q0已完成故障诊断,则转至步骤(6),否则若m0>1,则需要对子集Q0作进一步诊断,转至步骤5); 5)对子集Q0作进一步诊断和隔离:枚举所有测试,对其测试信息熵进行评估,搜索其中熵值最大的测试tk0,即{tk0|Hk0=max(Hj)},并选择tk0作为当前优选测试,将子集Q0再次分割为Q00和Q01两个更小的子集,其中j=0,1,…,m0。重新令Q0=Q00,Q1=Q01,重复步骤4); 6)以运行状态子集Q1作为对象开展分析,判断m1值:若m1=0,表示由于缺乏更多的系统测试信息,控制系统只能被隔离至当前得到最小故障模糊组;若m1=1,表示控制系统故障被精确隔离;出现上述两类情况,说明子集Q1已完成故障诊断,则返回上一层运行状态集合继续诊断,否则若m0>1,则需要对子集Q1作进一步诊断,转至步骤7); 7)对子集Q1作进一步诊断和隔离:枚举所有测试,对其测试信息熵Hj进行评估,搜索其中熵值最大的测试tk1,即{tk1|Hk1=max(Hj)},并选择tk1作为当前优选测试,将子集Q1再次分割为Q10和Q11两个更小的子集,其中j=0,1,…,m1。重新令Q0=Q10,Q1=Q11,重复步骤4); 8)基于信息熵最大的原则,不断重复步骤4)~7)描述的测试选择过程,直至能够将全部控制系统故障精确隔离或者隔离至最小模糊组。 由以上执行步骤可知,故障诊断测试路径规划实质上是将测试与系统故障间包含权值的相关性作为判据,构造完整故障隔离二叉树的过程,而当二叉树各左右分支对应权重相等或者接近时,代表着最优故障诊断路径规划。 设确定路径规划方案后,扩展故障集F*中元素fi经li次二分操作可被精确隔离或者隔离至最小模糊组,其中i=0,1,…,m。可定义故障诊断平均加权路径: (19) 采用文献[8]中的例子,为讨论方便起见,仍做如下规定:各物理或者逻辑功能单元S1~S15仅存在一类可能的故障,各测试点TP1~TP16仅包含一项测试。即某控制系统测试集为T={t1,…,t16},扩展故障集为F*={f0,f1,…,f15},对应的归一化运行概率为τ*={τ0,τ1,…,τ15}。采用有向图方式对该系统进行测试性建模如图2所示,对应的扩展全阶相关矩阵如式(20)所示。 (20) 图2 仿真系统测试性建模示意图 考虑如下3类情况:1)依据新技术、新方法全新设计控制系统且无相关功能单元故障经验数据,未经调试和试验验证,系统故障率较高;2)全新设计控制系统,但经过试验验证,系统故障率较低;3)继承性设计控制系统,有相关功能单元故障率统计数据,系统未经调试和试验验证,系统故障率高。 对于第1)、2)类情况,当无先验知识,无法确定各功能单元故障率时,可对故障率做平均分配,即: (21) 若(1)、(2)情况系统无故障运行概率分别为τ0=0.25和0.7,由式(20)可知,最终计算得到的各功能单元归一化扩展故障率分别为0.05与0.02;对于情况(3),设τ*={0.01,0.1,0.05,0.06,0.12,0.05,0.08,0.05,0.09,0.13,0.05,0.1,0.02,0.03,0.04,0.02},若各测试项间均需串行执行,则基于信息熵的故障诊断路径规划结果以二叉树方式表示分别,如图3~5所示。 图3 故障诊断路径规划仿真结果1 图4 故障诊断路径规划仿真结果2 图5 故障诊断路径规划仿真结果3 图中大矩形表示系统可能运行状态,小矩形内数字表示相应的运行概率,圆形表示对应选择的测试。 1)扩展故障集F*共包含m个元素,则理论上经过m-1次二分操作即可将全部系统运行状态精确隔离,即该方法实质上规定了故障诊断路径规划所需测试集元素数量的上限值。 图2对应的扩展故障集F*包含16个元素,状态精确隔离需要16-1=15次操作,而可用于路径规划的测试集为T中元素个数为16>15,故测试项目设置一定存在冗余。由图3和5亦可看出,仅应用了t1~t15进行故障诊断,t16为冗余测试; 2)故障诊断路径规划不同步骤中二分操作可由同一测试实施完成,即全部系统运行状态精确隔离所需的测试项目可进一步压缩。由图4可以看出,15次二分操作过程中,测试t2使用了2次,而t3和t16均为冗余测试。 可以进一步证明[9],若可以自由指定全阶相关矩阵D中元素的值,则全部系统运行状态精确隔离所需的测试数量n0满足: n0=log2m (22) 上式中m为扩展故障集F*中包含的元素个数。即该方法同时在理论上规定了故障诊断路径规划所需测试集元素数量的下限值。但受具体电路设计方案限制,很难指定任意测试与任意可能故障间的相关性,故实际工程应用中,故障诊断路径规划通常都比n0大; 3)通过对比图3~5可知,当电气系统运行可靠性较高时,应优先选择能够判断系统整体有无故障的测试项目,如图4中的t15,而电气系统自身运行故障率较高时,则首先对可能发生的故障模式进行隔离,这与电气系统故障隔离流程设计的直观认知一致; 图6 顺序测试诊断路径 4)在3种情况下,分别计算系统故障诊断平均加权路径。并与不采用路径规划方法,顺序使用测试t1~t15的诊断方案得到的值进行对比,其中顺序测试诊断路径如图6所示,计算结果如表1所示。 表1 3类规划平均加权路径L值 由表1可知,采用本方法进行路径规划后,与顺序测试相比,平均加权路径长度明显被压缩,从而证明了方法的有效性。 针对导弹武器对实战化要求不断提升这一客观背景,控制系统故障诊断技术也逐步从单纯追求测试覆盖性等功能指标向适应快速测发、快速维修等性能指标发展。基于测试信息熵的故障诊断路径规划方法能够通过分析控制系统测试性模型与装备历史先验故障信息,自适应地规划面向故障诊断的系统测试路径,大幅度缩短了导弹武器系统临射前的状态确认时间、提升故障检测与维修效率,具有非常显著的意义。2.3 路径规划方法
2.4 路径规划效果评估
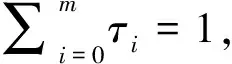
3 仿真分析
3.1 数据仿真

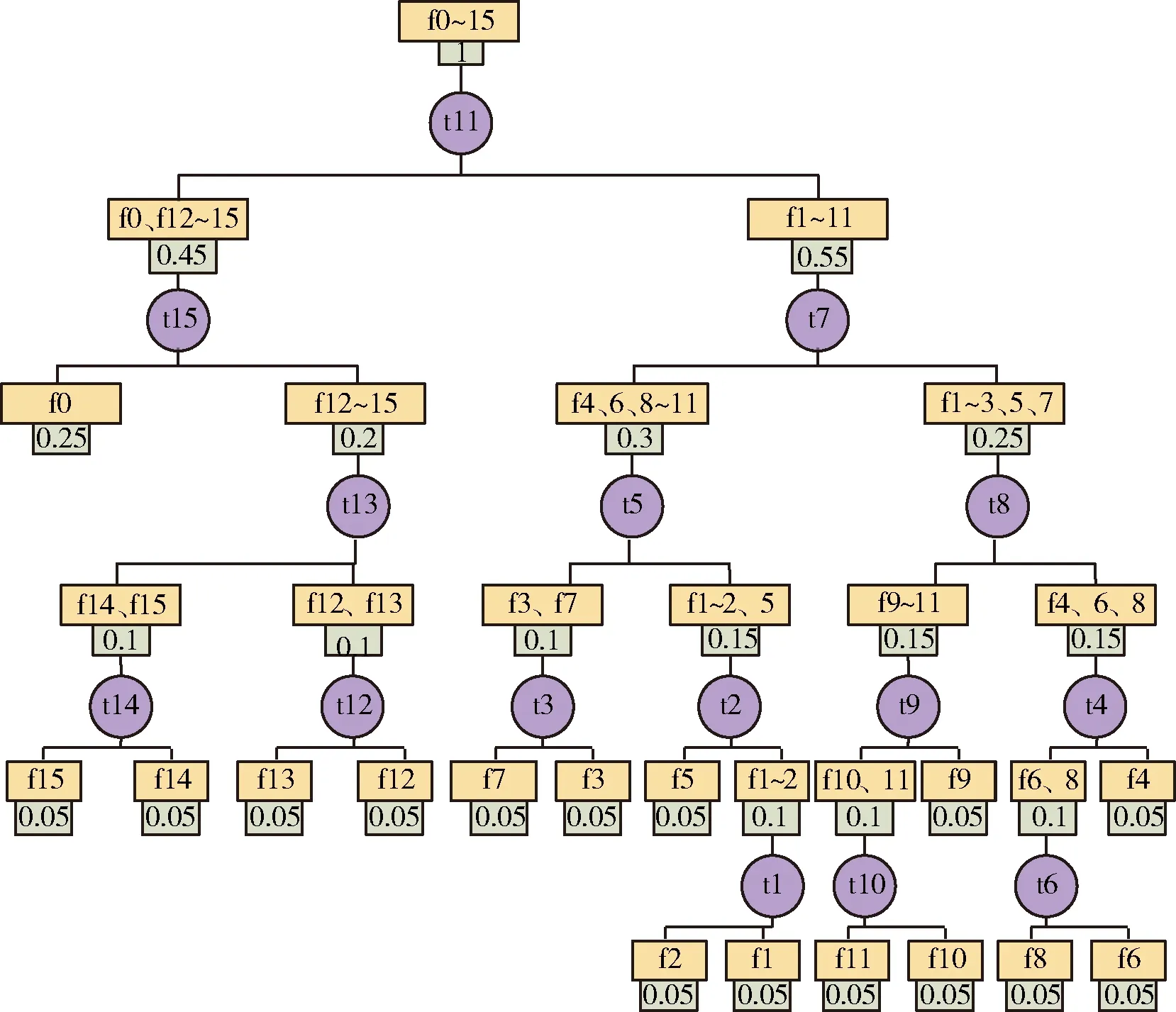


3.2 结果分析
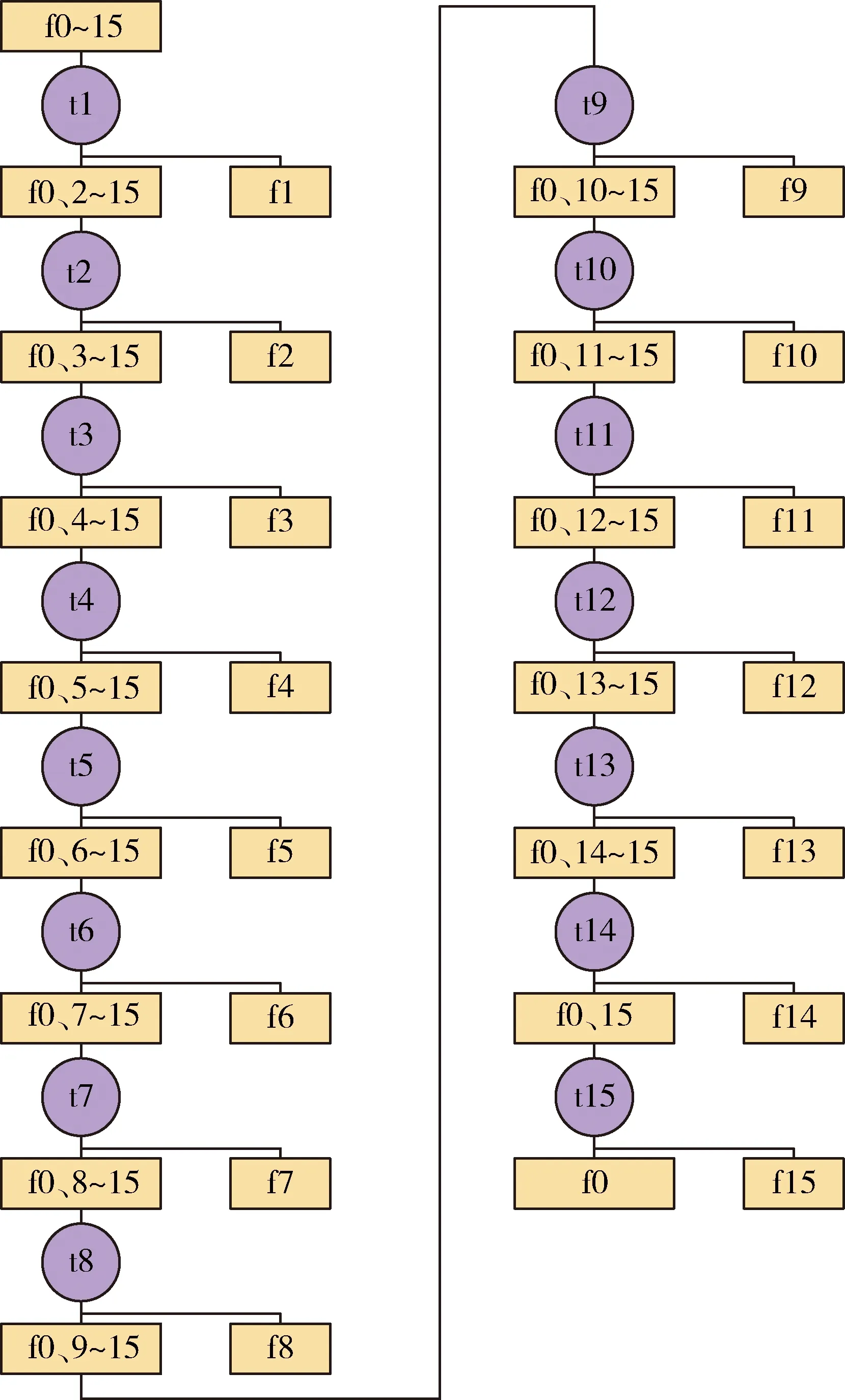

4 结论
