基于滑模控制理论的前向追踪制导律研究*

李之翰 王 琦 刘 阳 吴健健

南昌航空大学，南昌 330063

高超声速目标的拦截，对拦截器的拦截范围以及制导精度都提出了更高要求，而使用传统的比例导引法等方法拦截高超声速目标，难以达到制导精度要求，或成本过高。

为克服这些困难，Golan O M等人[1-2]提出了一种前向拦截的思想，即通过事先机动将拦截导弹置于目标前方的预测飞行弹道上，且飞行方向与其保持一致，由于拦截导弹具有较低的飞行速度，目标接近导弹，从而实现目标的拦截。该拦截方式将拦截器速度大于目标速度转化为拦截器速度小于目标速度，降低了拦截器的能量需求，从而降低控制难度和拦截成本。为研究空-空拦截器制导策略的导引品质，有必要研究前向追踪拦截方式的三维制导算法。张友安等[3]建立了迎面拦截三维模型，该模型中拦截器与目标对向运动，与前向追踪拦截有较大不同。文献[4]基于比例导引设计三维制导律，但他的制导律是建立在弹道线性化基础上，且比例导引的局限性大。赵振昊[5]基于准平行接近原理[6]设计制导律，他的制导律只需保持视线角为常数，不要求拦截器与目标速度方向一致，因此该制导律不仅仅适用于前向拦截。但是该制导律针对大机动目标的拦截所需过载较大，且制导末期视线角速度易发散。文献[7]运用辅助圆设计制导律算法，让拦截器沿辅助圆飞行进行拦截，文献[8]将神经网络PID控制应用于高超声速飞行器，这2种方法简单有效，但对目标机动没有很好的适应性。由于变结构控制对系统内部的参数摄动和外部扰动具有良好的鲁棒性，而被广泛运用于制导律的设计。文献[9]将变结构控制用于高超声速飞行器。文献[10-13]用变结构控制理论和模糊控制理论解决导弹等飞行器的拦截问题，取得了一定成果。文献[14]运用高阶滑模控制方法，有效抑制了抖动。文献[15]将滑模控制方法用于高超声速飞行器纵向轨迹研究。

通过建立前向追踪拦截模型，根据前向追踪拦截的限制条件，结合比例导引的优势，利用变结构控制对干扰具有自适应的特点，设计了一种滑模制导律。该制导律采用了控制拦截器与目标高度角成比例的思想，将低速拦截器始终控制在高速目标之前，具有很好的鲁棒性。同时，根据实际情况，拦截过程中目标通常是机动的，在目标5g机动的情况下进行仿真，验证制导律的精度。

1 前向追踪拦截模型

该数学模型为三自由度模型，将目标和拦截器视为质点，不考虑姿态变化；目标和拦截器的加速度矢量视为与速度矢量垂直，即法向加速度，加速度只改变速度方向，不改变速度大小。图1为弹目相对运动图，T和M分别表示目标和拦截器；xiyizi表示惯性坐标系；xlylzl表示视线坐标系；r为二者相对距离；vt和vm表示速度矢量；at和am表示加速度矢量；θ1和θ2分别表示视线倾角和视线偏角；α1和α2表示vt与视线的夹角；β1和β2表示vm与视线的夹角。通过图1可推导出前向追踪拦截的三维运动学和动力学方程，得到各相关参数的表达式。

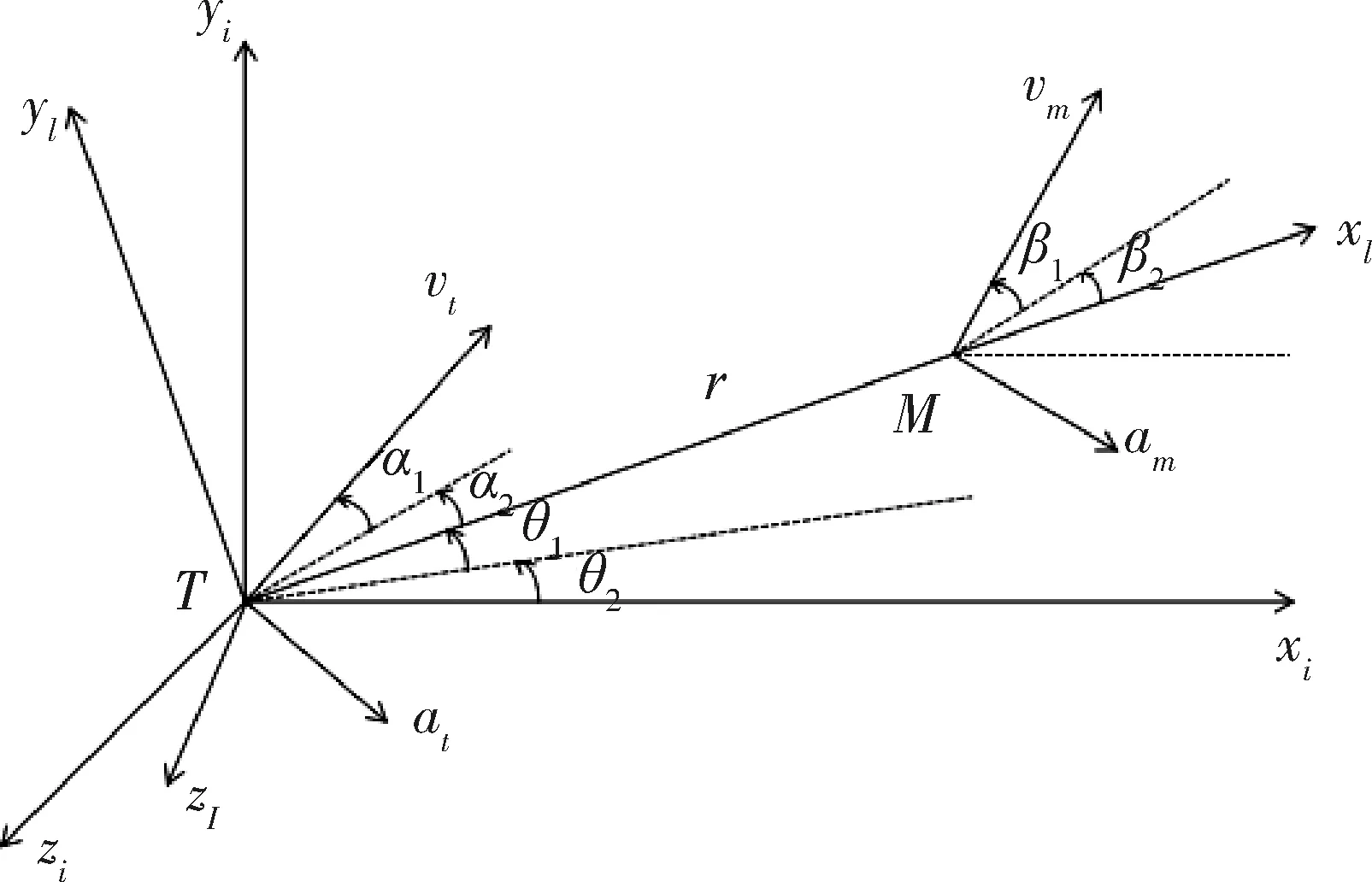
图1 弹目相对运动

(1)

(2)

(3)

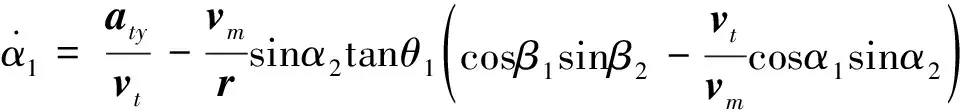
(4)

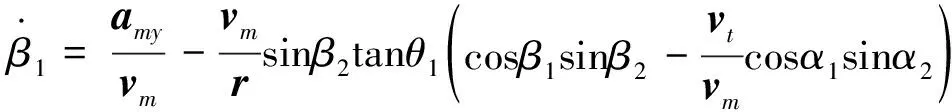
(5)

(6)

(7)

式中，aty和atz分别表示at在纵向通道和侧向通道的投影;amy和amz分别表示am在纵向通道和侧向通道的投影。

采用前向追踪拦截方式，要求拦截器速度小于目标速度，即|vm|/|vt|<1。

想要成功拦截目标，不仅要求在拦截处|r|→0，也要求目标和拦截器运动方向一致。即

(8)

(9)

导引的目的是达到式(8)和(9)要求的拦截点，在这一过程中，要求α和β成比例，即

β1=N1α1

(10)

β2=N2α2

(11)

其中，N1和N2是导引系数。这样就保证了β随α减小，使拦截器运动到目标前方，达到前向拦截的目的。

2 制导律设计

为达到式(8)和(9)要求的拦截点，本文根据滑模变结构控制理论，将拦截器的机动加速度amy和amz作为制导律进行设计。

导弹拦截系统是一种强耦合非线性系统，考虑如下非线性系统：

(12)

式中，X∈Rn为系统状态量;U(t)∈R为控制量;W(t)∈R为系统不确定项，即干扰项。假设不确定项W(t)有界，且满足0≤|W(t)|≤b。

根据滑模控制理论，设计滑模面为：

S=CX

(13)

其中，C∈R1×n为定常的，且Cg1(X,t)≠0。

Cg2(X,t)W(t)

(14)

根据文献[16]中设计的制导律，加以改进，得到如下制导律：

U(t)=Ueq+Us+Un

(15)

其中，

Ueq=-[Cg1(X,t)]-1[Cf(X,t)]

(16)

Us=-[Cg1(X,t)]-1Ksign(S)

(17)

(18)

式中，Ueq为等效控制项;Us为比例导引项，且为非负定;Un为不确定部分控制项。

定义Lyapunov函数:

(19)

而

(20)

从而有

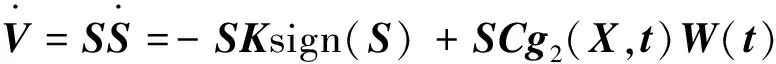
(21)

由上式可知，设计的滑模面满足Lyapunov稳定性定理，从理论上验证了制导律的可行性。

1)纵向通道

根据式(10)的限制条件，设计滑模面为：

S1=β1-N1α1

(22)

取系统状态量X=[r,β1,α1]T，控制量U(t)=amy，干扰量W(t)=aty，得状态方程：

(23)

其中：

f1=vmcosβ1cosβ2-vtcosα1cosα2

(24)

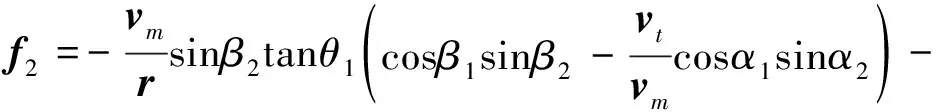
(25)

(26)

从而，

Ueq=-vm(f2-N1f3)

(27)

Us=-vmK2sign(S1)

(28)

(29)

可得纵向通道制导律：

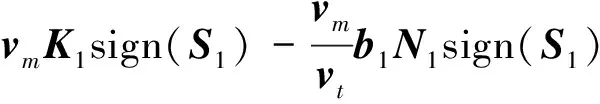
(30)

2)侧向通道

与纵向通道制导律设计方法同理，根据式(11)的限制条件，设计滑模面：

S2=β2-N2α2

(31)

取系统状态量X=[r,β2,α2]T，控制量U(t)=amz，干扰量W(t)=atz，得状态方程：

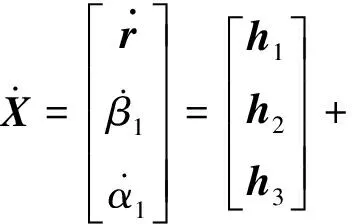
(32)

其中：

h1=vmcosβ1cosβ2-vtcosα1cosα2

(33)

(34)

(35)

可得侧向通道制导律：

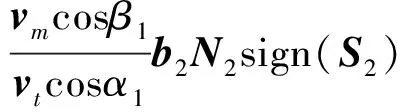
(36)

为降低抖振对滑模运动过程的影响，可以用饱和函数sat(Si)代替符号函数sign(Si)：

(37)

得到改进后的制导律：

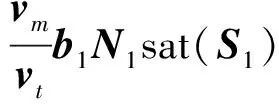
(38)

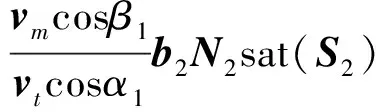
(39)

3 仿真结果

根据实际情况，设计的制导律应当能够拦截机动目标。在仿真过程中先让目标定速平直飞行；经过60s后给目标添加法向加速度，机动时间40s，前20s法向加速度为3g，后20s法向加速度为5g，2次机动方向相反；机动结束后，目标继续定速平直飞行。本文利用上述制导律进行拦截，分析其导引品质，对目标非机动与机动2种情况下的仿真结果进行了对比。

设置初始条件：vt=1700m/s，vm=1360m/s，N1=N2=2，b1=b2=100，目标初始坐标(0,20000,0)m，拦截器初始坐标(50000,10000,15000)m，许用过载为20g。本文拦截器发射方式为水平发射，只考虑拦截器定速飞行的情况。

从图2和3可以看出，目标非机动时，拦截轨迹很理想，拦截器在141.52s时成功拦截目标；目标机动时，拦截器能够随目标机动而机动，在末端制导中拦截器与目标运行轨迹逐渐重合，最终在127.49s时成功拦截目标。

从图4和5可以看出，过载最大值为17g，未超过许用过载，符合实际要求。拦截器在发射点达到最大过载，随后迅速降至0附近，之后过载随目标机动而变化，最终趋于0。

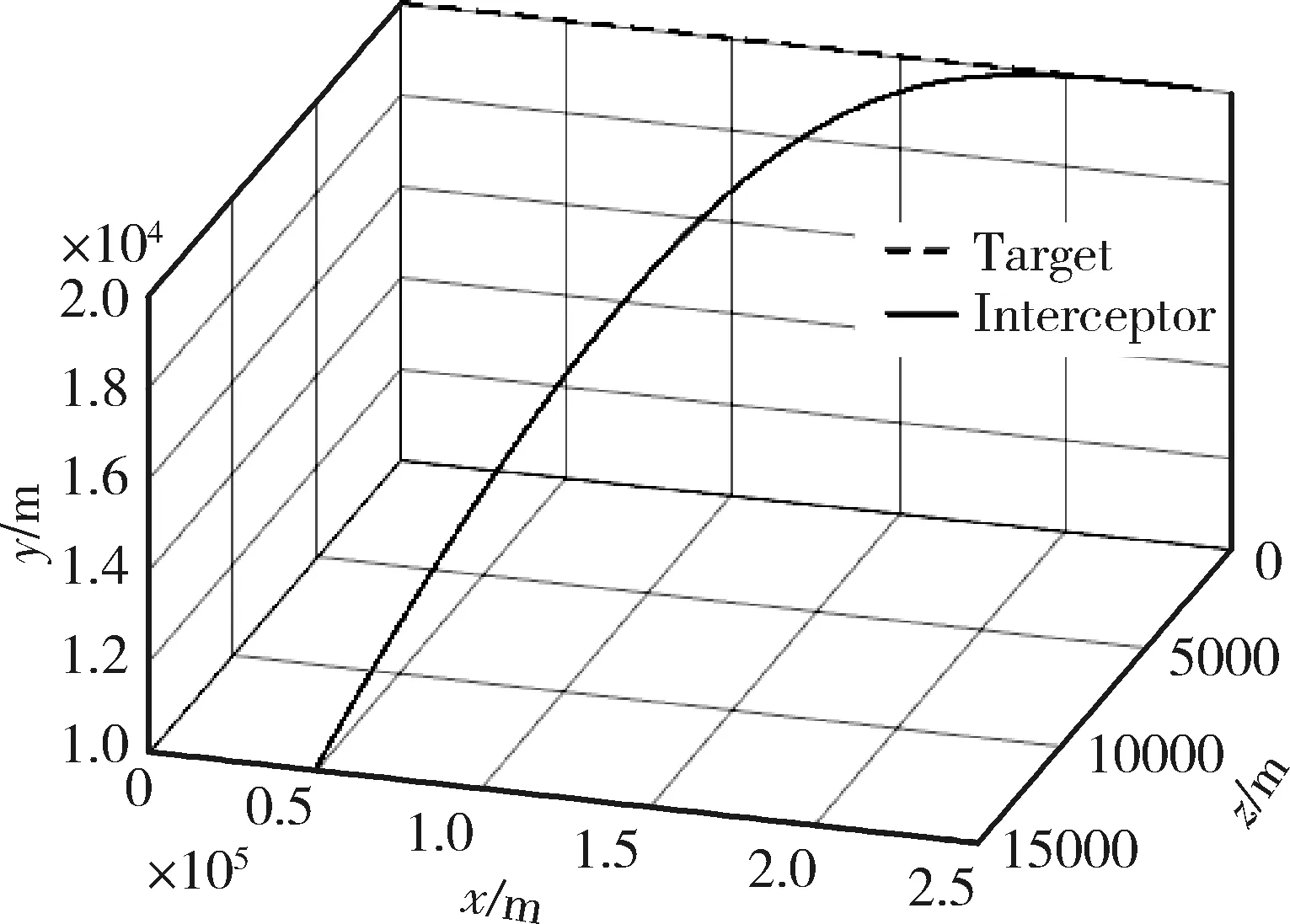
图2 相对运动轨迹(目标非机动)

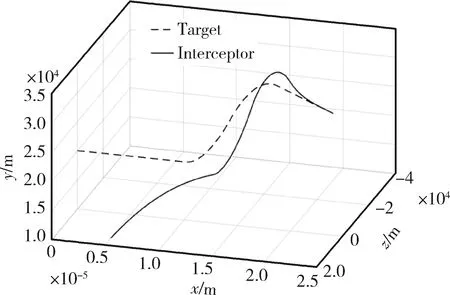
图3 相对运动轨迹(目标机动)

图4 法向过载(目标非机动)

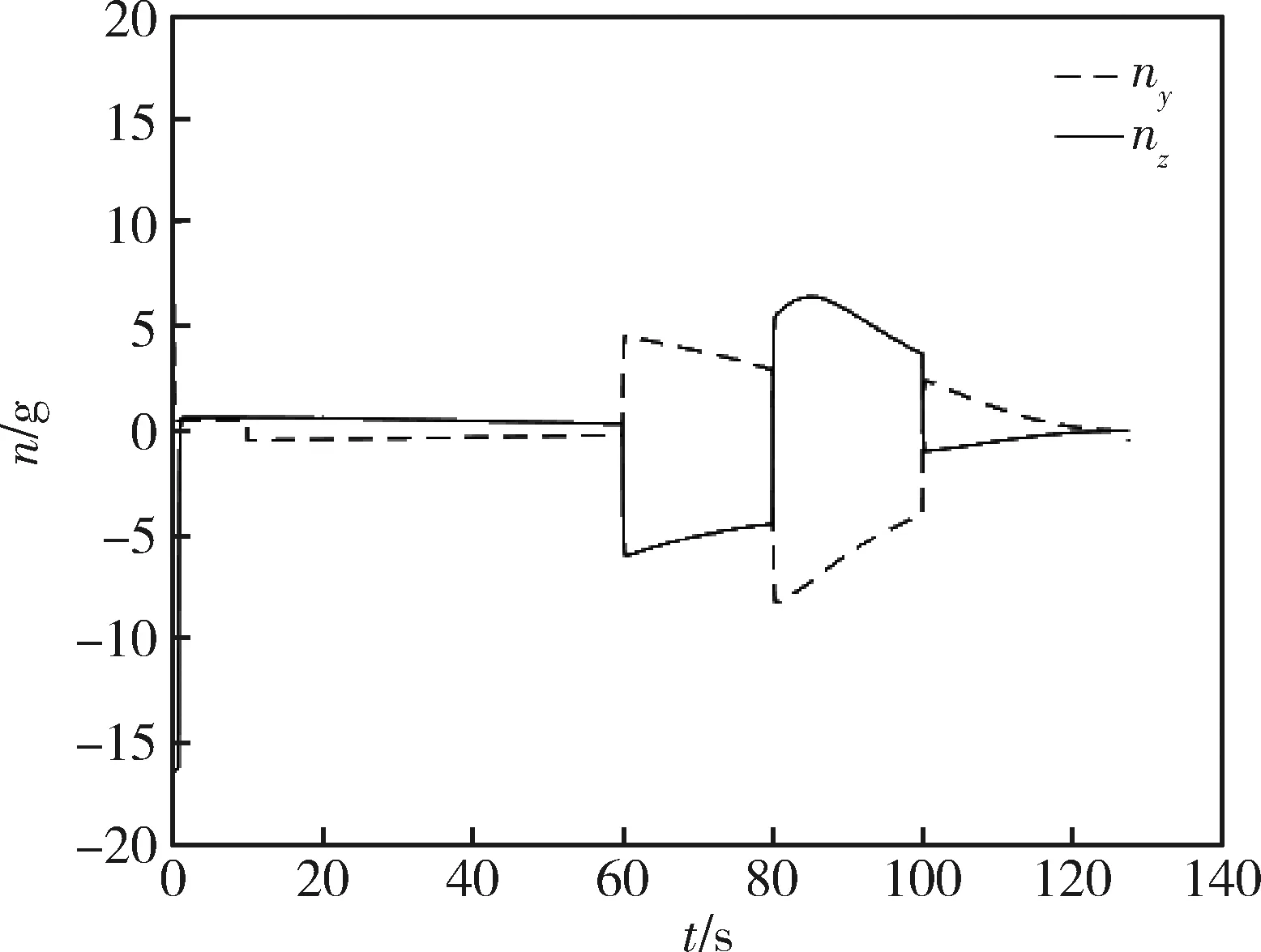
图5 法向过载(目标机动)

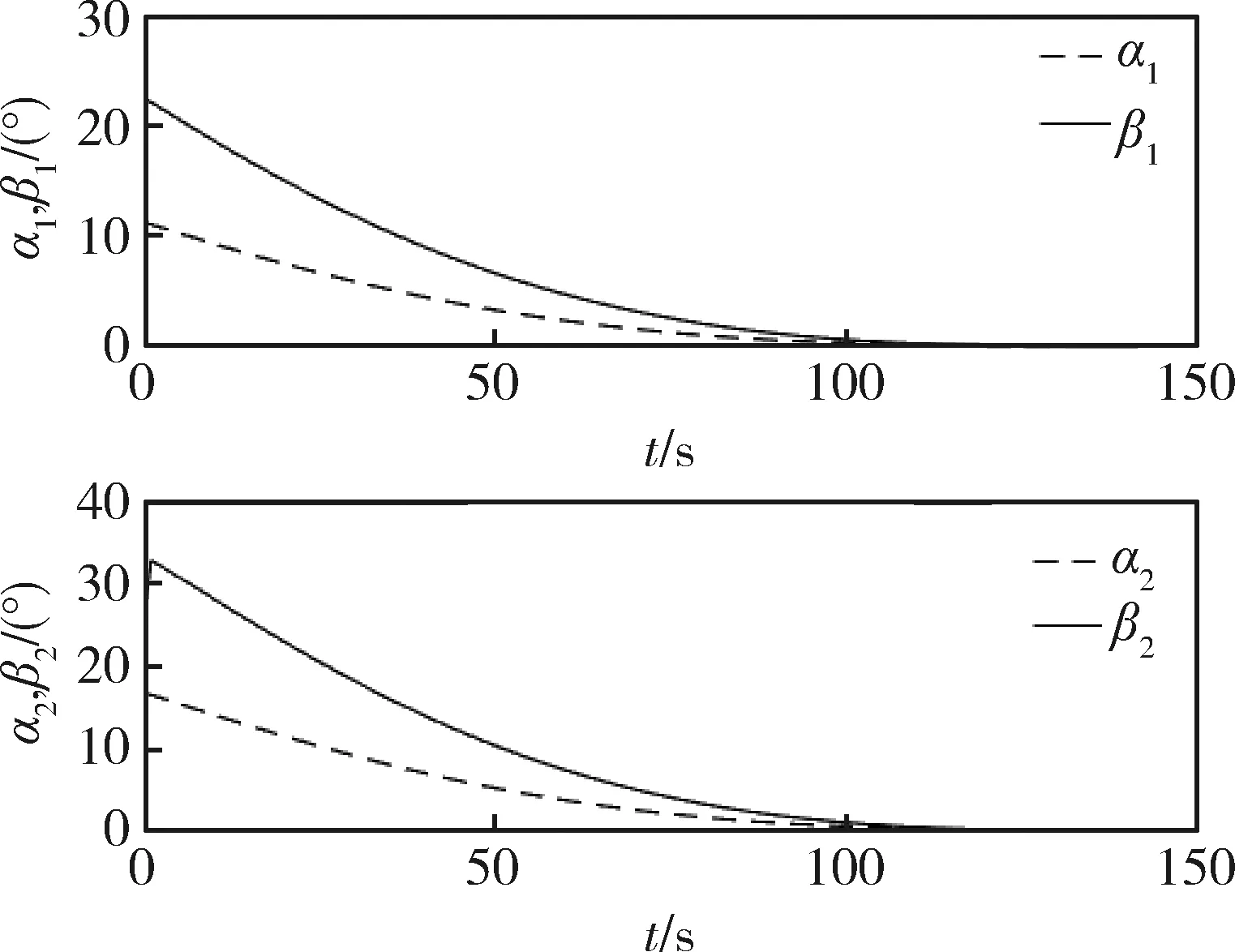
图6 α和β(目标非机动)

图7 α和β(目标机动)

图6和7显示的是速度与视线夹角α和β的变化趋势，可以看出，α和β是成比例变化的，最终都趋于0。

图8和9显示的是视线角的变化，θ1是纵向通道的视线角，θ2是侧向通道的视线角。图8说明，目标非机动时，视线角随时间递增，但其变化率逐渐减小，最终视线角趋于定值；图9说明，目标开始机动后，视线角迅速增大又迅速减小，目标结束机动，视线角变化率减小，视线角最终趋于定值。

图8 视线角(目标非机动)

4 结论

通过分析前向追踪拦截过程的特性，建立前向追踪拦截三维运动模型，基于滑模控制理论设计制导律，对拦截过程进行了仿真。仿真结果表明，该方法能够让低速拦截器成功拦截高速目标，且目标机动时拦截器能自适应改变运动轨迹，一定程度上解决了比例导引法存在的控制难度大、制导精度不高的问题；本制导律对加速度干扰具有较强的鲁棒性，适用于对高超声速目标的拦截；通过估计目标的机动加速度，证明了其也适用于对复杂机动目标的拦截。