含径流式水电系统安全经济调度的矩不确定分布式鲁棒优化方法

冷 鹏，陈 众，伍雅娜，汤 俊

(智能电网运行与控制重点实验室(长沙理工大学)，湖南 长沙 410004)

0 引言

相对其他清洁能源而言，水电资源具有更高的经济和社会效益。径流水电站因无调节库容而调节能力很差[1]，其出力直接受天然来水影响而呈现明显的随机性。

因市场价格、风力、来水量等引起的发电出力不确定性的调度问题可用机会约束规划[2]、条件风险价值[3]、蒙特卡罗方法等方法[4]，协调风险与利润以实现最优决策。这些处理不确定性问题的方法是基于概率统计学的随机规划方法[5]，都是在确定性分布的基础上建模，需要得知随机变量的完整分布统计特性。一般通过对历史数据统计得出概率分布函数，其矩即期望、方差、协方差等均为确定值。另一类处理不确定性问题的方法是鲁棒优化方法[6]，其不需要知道随机变量的概率分布函数，只需得知参数所属区间[7-8]。一般用不确定集合刻画随机变量的不确定性，并建立考虑随机变量在所给定集合中任意变化时的最严重情况下的min-max优化模型[9]，但是这类方法未能有效利用一些可获取的概率统计信息。

径流水电的出力在一定范围变化[10]，且具有概率分布特性[11]。虽然径流水电出力难以用某一确定概率分布函数进行刻画[12]。根据文献[13]并参照风电出力特点可知，径流水电出力为矩参数在一定范围内波动的随机量，故考虑采用矩不确定分布式鲁棒优化方法出力含径流水电系统的安全经济调度问题。

区别于随机规划方法以确定的概率分布函数描述不确定变量，也区别于传统鲁棒优化方法用区间不确定集合直接描述变量范围，矩不确定分布式鲁棒优化方法(Distributional Robust Optimization Under Moment Uncertainty，DRO-MU)结合随机规划和鲁棒优化思想的一种处理含随机变量优化问题的方法，它通过不确定集合描述其矩即期望与协方差[14]，可以用于解决含径流水电等不确定出力机组的系统优化调度问题。

1 矩不确定分布式鲁棒优化方法

1.1 矩不确定集合

设凸优化问题的一般形式为：

(1a)

s.t.φ(x,ξ)≤0

(1b)

式中：x为决策变量；ξ为某一类问题的参变量；χ为可行解的凸集；h(x,ξ)、φ(x,ξ)均为关于x、ξ的凸函数。从该优化问题可知：

(1)如果参变量ξ为确定值，则该问题是一般的凸优化问题；

(2)如果参变量ξ为随机变量，则该凸优化问题为不确定性优化问题。

针对情况(2)不确定性优化问题，通常的处理方式是通过对不确定变量长期的实测数据统计、分析、拟合得出其概率分布函数，由此求得的期望、协方差等矩是确定的。但是，在实际应用中，不确定变量(如风电短期出力)规律性不强，波动大，难以用单一的概率分布进行准确刻画，但是其分布的矩却是在一定范围内波动的。因此，假设其期望、协方差的取值属于特定集合D[15]。其结构如下：

(2)

式中：μ0为随机变量ξ的预估期望；Σ0为随机变量ξ的预估协方差，Σ00表示半正定；γ1、γ2为该集合的半径限制参数，γ1≥0，γ2≥1；ψ表示在可测空间上的所有概率密度集；S是由随机变量ξ所有可能取值组成的样本空间，S⊂Rm。

不确定集合D中第一个约束条件表示随机变量ξ包含于S的概率为1；第二个约束条件表示随机变量ξ的实际期望处在椭球球心μ0(即预估期望)、椭球半径为γ1的椭球不确定集内；第三个约束条件表示随机变量ξ的实际协方差处在矩阵不等式限定的半定锥不确定集内。

1.2 目标函数对应的min-max函数

针对情况(2)的不确定优化问题，首先根据均值方差理论考虑其目标函数的期望值最小，将式(1a)写成以下形式：

(3)

引入鲁棒优化思想，在随机变量概率分布函数的期望、协方差属于不确定集合D的基础上，将上述目标函数转化为考虑其最严重情况下的min-max问题[15]：

(4)

其中，E[h(x,ξ)]为目标函数h(x,ξ)的期望。

1.3 不等式约束的条件期望预处理及其对应的min-max函数

不等式约束中含随机变量时，直接取不等式约束函数(1b)的期望进行处理会造成不等式成立的概率水平、不等式越界的分位点及越界后的均值均不明确，不能准确反映不等式成立概率水平。而采用条件期望预处理不等式函数，能有效刻画不等式小于分位点的概率及越界后的超额平均值，故可先求取φ(x,ξ)在概率水平β下的条件期望。

若随机变量ξ的概率密度函数为p(ξ)，则条件期望表达如下：

(5)

式中：qβ(x)表示分位数；β表示置信水平，其具体表达的是一个概率水平。式(5)是指函数φ(x,ξ)在以不小于β概率水平下大于qβ(x)的期望值，即条件期望。

式(5)难于解析，可引入函数Fβ(x,α)来计算其条件期望值[16-17]：

(6)

式中：α为引入的辅助变量。

结合式(6)的条件期望值，引入鲁棒思想，在随机变量概率分布函数的期望、协方差属于特定集合D的基础上，考虑不等式约束(1b)最严重情况下的min-max问题[18]：

(7)

1.4 分布式鲁棒优化模型的对偶转换

综上所述，一般含随机变量的凸优化问题对应的矩不确定分布式鲁棒优化模型如下：

(8)

此时的矩不确定分布式鲁棒优化模型为NP难问题，无法直接求解出其最优解。采用拉格朗日对偶原理[19]，将其转换成确定性的半定规划模型，便于求解。目标函数转化后的模型如下：

(9)

(10)

因此，通过对偶转换，矩不确定分布式鲁棒优化模型变换为如下半定规划问题：

(11)

2 含径流水电出力矩不确定的系统安全经济调度

2.1 水火电系统安全经济调度一般模型

以常规火电机组发电成本最小为目标函数，同时考虑发电机出力上下限约束、系统功率平衡约束、线路潮流安全约束，建立接入径流水电电力系统安全经济调度的一般模型：

(12a)

(12b)

eTPf+eTPh-eTPd=0

(12c)

|PL|≤PLmax,L=1,2,…,l

(12d)

2.2 考虑径流水电出力矩不确定的优化模型

2.2.1 径流水电出力的矩不确定集合

结合矩不确定分布式鲁棒优化方法，考虑径流水电出力Ph的随机性，假设其分布Fh的均值、协方差取值范围属于特定集合D：

(13)

式中：μh为随机变量Ph的预估均值；Σh为随机变量Ph的预估协方差，Σh≻0；γ1、γ2为该集合的半径限制参数，γ1≥0，γ2≥1；ψ表示在可测空间上的所有概率密度集；S是由随机变量Ph所有可能取值组成的样本空间，S⊂Rm。

2.2.2 目标函数对应的min-max问题

结合矩不确定分布式鲁棒优化方法，在μh和Σh属于特定集合D的基础上，将系统安全经济调度模型(12)中目标函数以式(3)的方法转化为考虑其最严重情况下的min-max问题：

(14)

2.2.3 线路安全潮流约束对应的min-max问题

模型(12)中含随机变量Ph的线路潮流安全约束，直接对其求取期望不能反映不等式成立概率水平。因此，对线路潮流安全约束不等式(12 d)求取条件期望值作为预处理。

支路潮流方程式为：

PL=BLMX(Pf+Ph-Pd)

(15)

式中：M为节点支路关联矩阵；BL为各支路导纳组成的对角矩阵；X=B-1，B为节点导纳矩阵。令H=BLMX=(H1H2…Hj…Hl)T，式(12 d)等价于：

|H(Pf+Ph-Pd)|≤PLmax

(16)

H为节点对线路的灵敏度系数矩阵，式(15)即线路安全灵敏度矩阵约束。系统中所有支路均需满足式(14)，选择其最大值所在的支路作为参考，若该支路满足式(15)，则所有支路均满足，故该不等式约束也写成：

max[|H(Pf+Ph-Pd)|-PLmax]≤0

(17)

假设第j条支路取值最大，定义电网安全域函数：

(18)

则线路安全灵敏度矩阵约束可写成：

Hj(PG,PS,PD)≤0

(19)

根据式(6)～(8)，式(18)等价于：

(20)

因此，径流水电出力矩不确定的分布式鲁棒优化模型为：

(21)

3 对偶转换及其半定模型

3.1 目标函数的对偶转换

运用矩不确定分布式鲁棒优化方法处理不确定性优化问题时，考虑到模型等式约束中的随机变量不易于处理，于是将系统功率平衡约束(12c)代入目标函数，消去随机变量。

假设节点1为系统的平衡节点，则系统功率平衡约束等价于：

(22)

将式(22)代入目标函数中：

(23)

其中：

根据式(10)，采用对偶理论将目标函数(22)化成如下的半定规划问题：

min(Q,q,r,t)r+t

t≥(γ2Σ+μμT)·Q+μTq+

Q0

(24)

式中：Q、q、r、t为模型对偶过程中产生的新的变量；Q为不对称矩阵，Q∈Rm×m；q∈Rm；r,t∈R。

由半正定的定义可知，式(24)中第一个不等式约束等价于：

(25)

3.2 线路安全灵敏度矩阵约束转换

根据式(11)，采用对偶原理将预处理后的不等式约束(20)化成如下的半定规划问题：

(26)

式(26)中第一个不等式约束可写成：

(27a)

(27b)

由半正定的定义可知，式(27a)、(27b)等价于：

(28a)

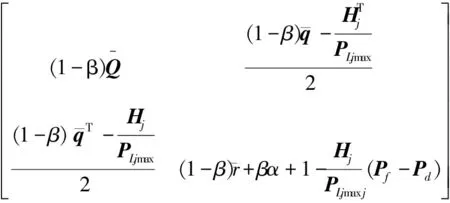
(28b)

3.3 转换后的半定规划模型

通过对偶转换，原径流水电出力矩不确定的分布式鲁棒优化模型转换成确定性的半定规划模型：

(29)

由模型(28)可看出，转换后的半定规划模型求解简单，只需用计算工具求解满足约束条件下的常规机组发电成本最小。

4 算例与分析

4.1 仿真系统

为验证矩不确定分布式鲁棒优化模型的有效性，对IEEE- 30节点系统进行分析计算，取功率基准值为100 MVA。在MATLAB中采用YALMIP进行求解。系统内有6台常规机组，节点1为平衡节点，径流水电机组在22、25节点处接入系统。其中22节点预测出力0.8 p.u.，预测偏差值的波动方差取0.2；25节点预测出力0.4 p.u.，预测偏差值的波动方差取0.12。系统总负荷为2.834 p.u.。其他基准要求为：γ1=0.1，γ2=1.1，α=0.92。系统数值仿真均是在基准要求上逐个改变相应参数进行仿真讨论。

4.2 仿真结果分析

(1)不确定集范围限制参数γ1、γ2对总成本的影响

从图1、图2可以看出，随着不确定集范围的限定参数γ1和γ2的增大，系统火电机组的发电成本也在增大。它们的值越大，表明径流水电出力预测准确性越差，其不确定性对系统安全性的影响增大。这会导致系统调度员采用更保守的运行方式，牺牲系统一定的经济性来满足系统安全可靠运行的要求。

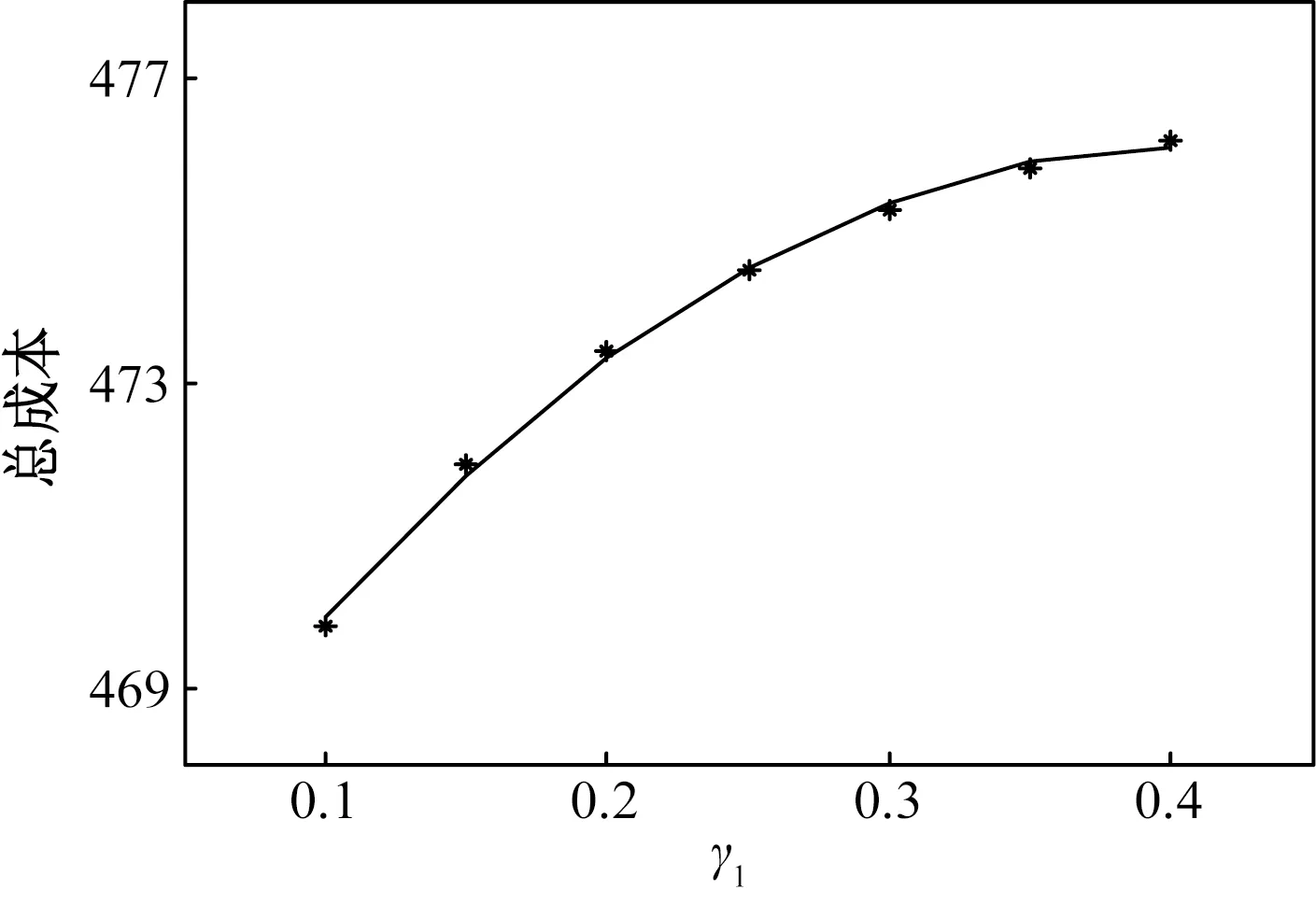
图1 总成本随γ1值的变化曲线

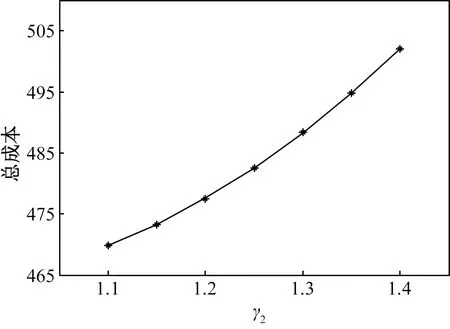
图2 总成本随γ2值的变化曲线

(2)不同置信水平下的调度方案

置信水平反映地是满足条件期望约束的概率水平。表1给出不同置信水平下的调度方案。由图3可看出，系统的常规机组总发电成本随着置信水平的提高而增大，因为置信水平越高，电网运行安全性越高，从而系统发电成本也会增加。

(3)分布特性未知时与传统鲁棒优化的不同特性

现实中存在难以得知随机变量分布的情况，此时随机规划方法不适用，因而可采用矩不确定分布式鲁棒优化方法或传统鲁棒优化方法。

表1 不同置信水平下的调度方案 p.u.

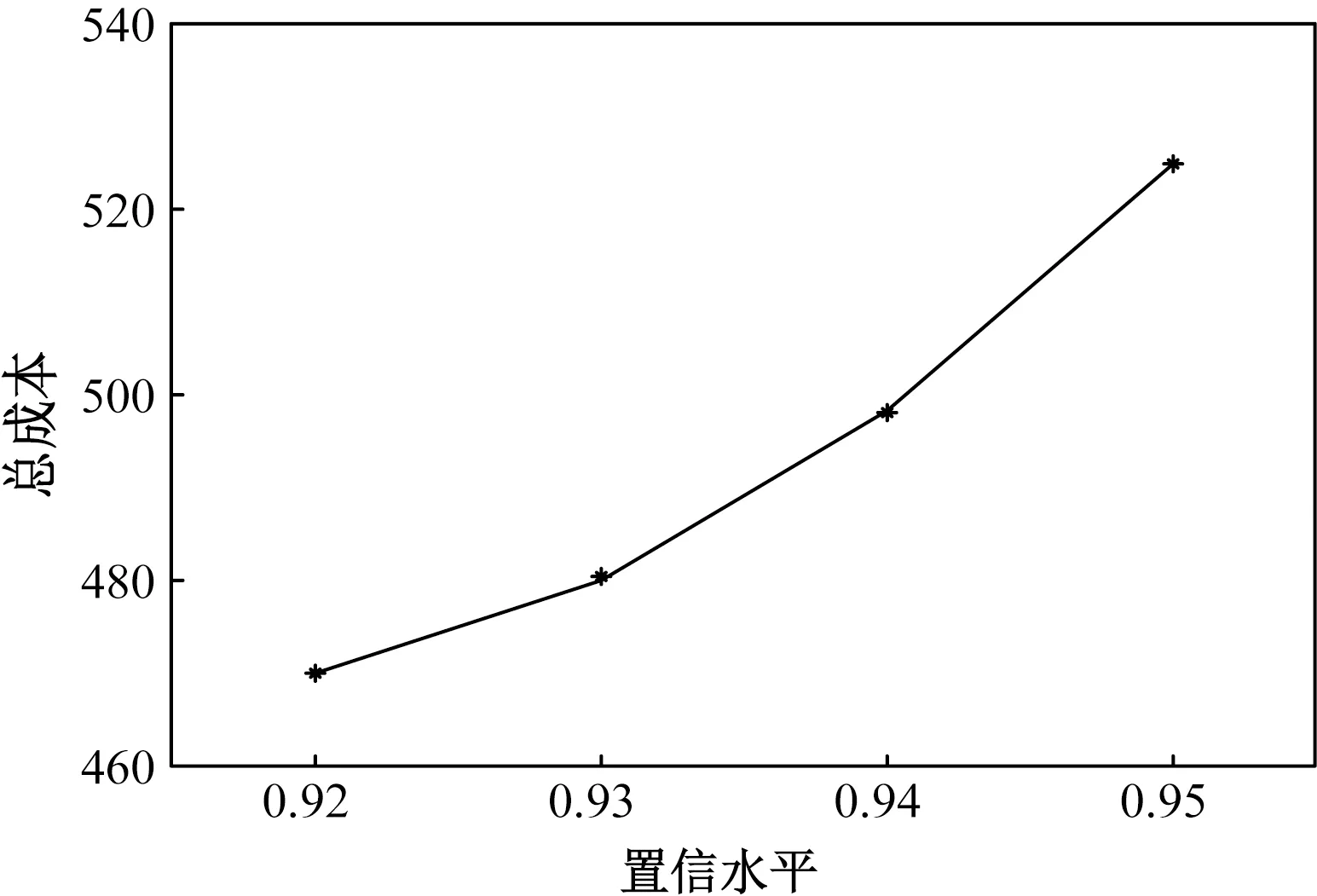
图3 总成本随置信水平的变化曲线

以径流水电为例，由于出力受气象因素等多因素的综合影响，其预测值可能不服从现有某一概率分布。如图4所示，当对该预测值的预测偏差进行分布拟合，利用KS检验(Kolmogorov-Smirnov test)验证样本的观测经验分布是否服从假设分布。

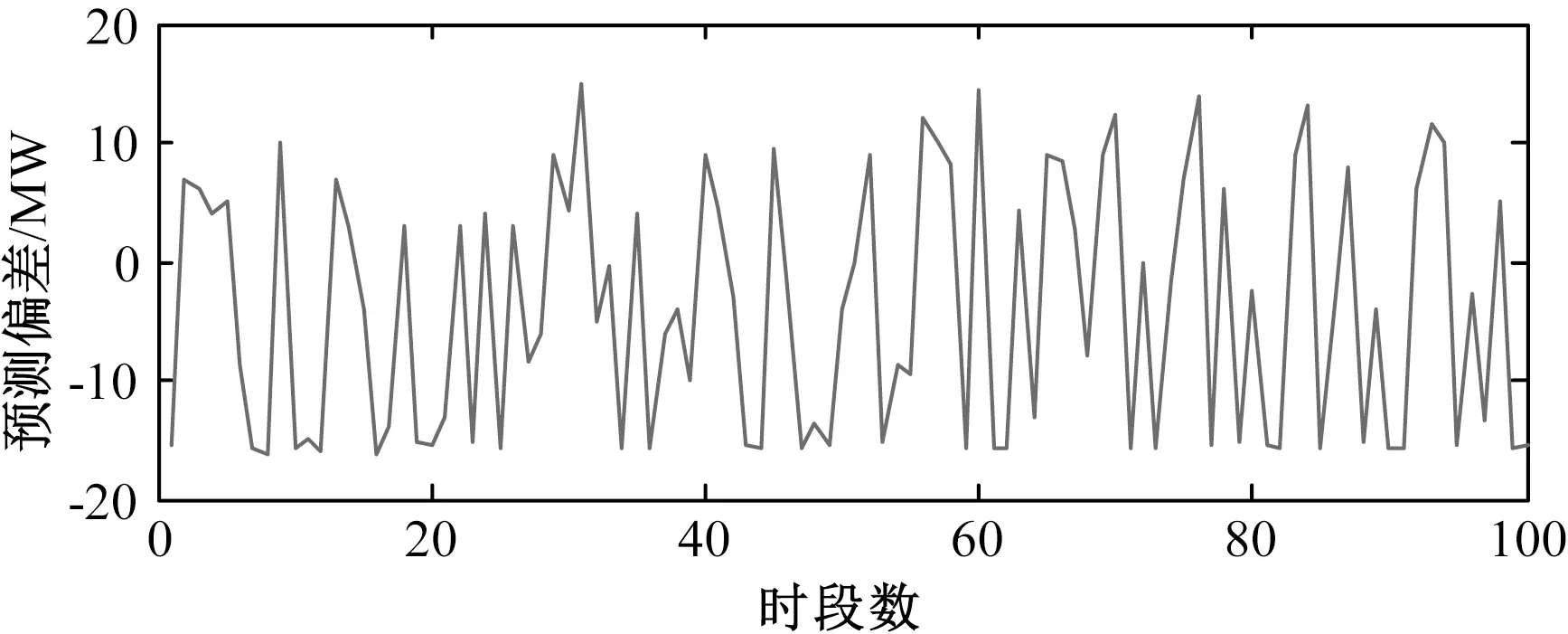
图4 某预测出力值下的实际偏差

由表2可以看出，所有假设分布的显著性水平均低于设定值。因此认为该径流水电出力预测偏差数据样本不服从所有假设的常见分布。

表2 拟合分布的KS检验结果

当径流水电出力预测偏差数据不服从已知分布时，基于确定性分布的CVaR方法无从刻画，不能求解。而文中的矩不确定分布式鲁棒优化是基于矩参数进行建模求解，其矩参数比较容易获取，不涉及具体分布类型，对分布未知的预测数据仍具有适用性。

(4)与矩确定的CVaR方法对比

矩不确定分布式鲁棒方法在随机规划的基础上，通过不确定集合描述其矩的不确定性，其对不确定性的描述更全面。在能够获取随机变量完整分布特性的情况下，以CVaR方法为例进行对比分析。

正态分布下CVaR方法计算的调度方案如表3所示，其总成本为467$，与基准要求下DRO-MU所得方案相比偏低。这是由于CVaR方法没有考虑分布的不确定性，导致发电成本较低的平衡机组出力比矩不确定分布式鲁棒方法的调度方案大，故总成本偏低。

表3表示矩不确定鲁棒优化方法所得的调度方案与CVaR方法所得调度方案在不同正态分布下条件期望约束满足的实际置信水平，即在给定调度方案下条件期望约束成立的实际概率。

表3正态分布下CVaR方法的调度方案

p.u.

由表4可知，在基准要求下，两种方法所得调度方案的置信水平均大于0.92，但采用CVaR方法所得调度方案在分布发生变化时，部分条件期望约束条件可能不满足所要求的概率水平；而矩不确定分布式鲁棒优化方法均能达到要求的概率水平。这是由于矩不确定分布式鲁棒优化方法在建模时就考虑到了分布的不确定性，能有效计算不确定集范围内的安全性所需要达到的要求，故矩不确定分布鲁棒优化方法的调度方案安全性更高。

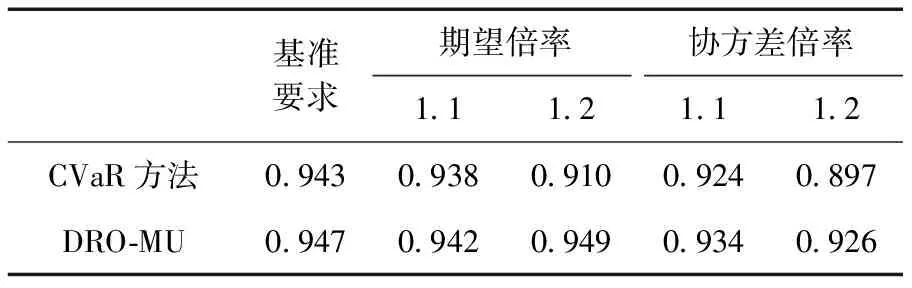
表4 矩参数发生变化时实际置信水平对比

5 结论

矩不确定分布式鲁棒优化方法既适用于带有矩不确定随机变量的电力系统优化调度问题，也适用于随机变量概率分布未知的情况。对于分布未知的问题，该方法与传统鲁棒优化的在数学求解方法上有本质区别，但计算结果均与不确定集参数的选择相关；对于分布已知时，该方法比现有随机规划方法更充分利用了分布参数及其可能存在的随机性。本文中采用矩不确定分布鲁棒优化方法所得方案与具体分布下采用CVaR方法所得方案相比，调度成本稍高，但考虑矩的不确定性，方案安全性更强。该方法也可用于求解其他具有随机性特点如价格、负荷、风电等参数的不确定性问题。