基于Kriging模型的重力坝可靠性分析
2019-01-07周方明潘红梅占良红王
周方明,潘红梅,占良红王 锋
(1.宿州学院资源与土木工程学院,安徽 宿州 234000;2.南昌大学建筑工程学院,江西 南昌 330031;3.江西水利职业学院,江西 南昌 330013)
0 引 言
我国现役混凝土坝无论是数量还是坝高均居世界首位,这些重力坝工程健康服役直接关系到整个水工程的安危,已成为关乎国计民生的重大公共安全问题[1]。因此,对重力坝的可靠性评估研究是目前大坝安全控制领域高度关注的重要科学问题。
重力坝特殊的结构性质及其复杂的工作环境,决定了对其进行可靠性分析的复杂性。自1926年德国学者迈耶最早将概率论引入到分析结构可靠度以来,结构可靠度理论的运用取得了重大进展[2]。我国首次把结构可靠性分析方法引入大坝可靠度计算的是河海大学“水工可靠度”科研组。武清玺等[3]研究提出了基于有限元法的重力坝可靠性分析,并进一步计算了重力坝抗滑稳定的可靠性;吴世伟等[4]基于概率可靠度理论对重力坝最大可能破坏模式进行了探讨,提出了地基、坝体、地基与坝体交界面3种主要的破坏模式。将概率可靠性理论用于评估重力坝的安全状态时,需突出解决好两大问题:一是在重力坝可靠性分析过程中其参数通常选用设计标准值,未考虑重力坝服役期间在内外环境及自身老化持续影响下,其参数因发生演化而改变;二是对于重力坝这种极为复杂工程,其极限状态方程常表现为高度非线性且难以用显式的方程给以刻画,采用材料力学分析的手段构建极限状态方程与重力坝真实响应存在较大误差,这些因素势必影响可靠性真实计算结果。
工程中常用响应面法(RSM)以二项式模型来近似拟合其极限状态方程,江胜华等[5]运用加权响应面法,计算了重力坝各断层抗滑稳定的可靠指标,并与安全系数进行了比较,表明其安全系数与可靠指标并非存在完全的对等关系。然已有研究表明,在高非线性问题中,RSM法需大量的计算工作,且对于高非线性可靠性问题常出现无法收敛和精度不足的情况[6]。Gaspar等[7]指出,Kriging模型较其它方法具有更优的预测能力及灵活性,与多项式回归模型相比,Kriging模型求解的失效概率更为准确。文献[8]基于Kriging模型精确拟合了某航空结构的极限状态方程,并对其可靠性实现了高效计算。
据此,考虑到重力坝参数随服役而发生演化改变,本文基于重力坝参数的衰减函数获取重力坝服役后其真实概率分布信息。在此基础上,借鉴Kriging模型强预测及拟合能力,探研重力坝极限状态方程精确拟合方法,并根据可靠指标几何定义,拟建立重力坝坝体单元强度破坏和沿坝基面抗滑失稳的概率可靠度优化模型,以实现深入分析重力坝可靠性。
1 重力坝Kriging模型的建立及检验
1.1 Kriging模型的基本原理
Kriging模型是一种统计近似模型[9],对于任意输入变量x∈Rn与响应值y有如下关系,即:
(1)
式中:f(x)T=[f1(x),f2(x),…,fp(x)]为回归模型,常采用二次多项式函数形式;β=[β1,β2,…,βp]T为回归模型系数;z(x)为随机误差,其均值为0、方差为σ2。
假定随机抽样m个计算样本点组成的矩阵为S=[s1,s2,…,sm]T,si∈Rn(i=1,2,…,m),其每个样本点组成的响应值矩阵为Y=[y1,y2,…,ym]T。通过精确模拟样本点矩阵S和响应值矩阵Y之间对应规律,可借助MATLAB强大计算优势完成Kriging模型的建立。
1.2 重力坝Kriging模型
以2.1节所述Kriging模型理论为基础,通过合理选取重力坝计算参数和功能函数(响应函数)形式,构建重力坝的Kriging模型。本文重点考虑重力坝单元强度破坏和沿坝基面抗滑失稳两种破坏形式。
本文参考文献[10],根据单元的第一、第二和第三主应力(σ1、σ2和σ3)建立单元破坏的响应值函数,即:
(2)
式中:g(x)为重力坝单元强度的功能函数(响应值);α=ft/fc;ft和fc分别为重力坝单元的抗拉强度和抗压强度。
根据坝体与坝基抗滑面上所有单元应力,建立失稳破坏的响应值函数,即:
(3)
式中:n为抗滑面上单元总数;f和c为分别为材料的摩擦系数和粘聚力;σyi和τxyi分别为单元i的正应力和剪应力;bi为单元i沿滑动面的边长。
1.3 Kriging模型的检验
Kriging模型近似拟合重力坝极限状态方程,必然与真实响应面存在一定误差[11]。本文用复相关系数来检验Kriging模型拟合效果,即:
(4)
(5)

由定义可知R2介于0到1之间,其中R2越趋于1表明拟合效果越佳。其检验步骤如下:
Step1:根据重力坝参数统计分布信息,抽样获取足够样本点,得到总样本点集U,再从U中随机抽取适量样本点组成子样本集C1,并根据子样本集C1信息结合有限元仿真响应建立Kriging模型。

Step3:根据复相关系数R2判断所建Kriging模型是否达到预期精度要求,符合则选用该模型,否则返回Step1重新选择子样本集C1重复以上步骤,直至满足精度要求。
2 重力坝可靠指标β计算模型
2.1可靠指标β优化模型
根据经典的可靠度理论,定义可靠指标β是在标准正态空间中,原点O距极限状态曲面最短距离,验算点P*为极限状态曲面一点,如图1所示。对于任一观测点x都唯一对应一响应值y=g(x),若在保证y*=0(极限状态曲面)前提下找到某一观测点x*在标准正态空间中距原点最近,则观测点x*即为验算点P*。则可靠指标β的计算可转化为一数值优化问题,即:
(6)
式中:x*为标准正态空间设计验算点;y=g(x)=0为Kriging模型拟合得到极限状态方程;ε为允许误差,取0.000 1。考虑到Kriging模型只是近似模型,因此人为设定一个极小的允许误差ε=0.000 1。对于式(6)可在MATLAB中调用fmincon函数优化求解,具体操作步骤为:①根据计算参数建立目标函数my_fun;②对拟合Kriging模型全局化(global dmodel,dmodel为拟合Kriging模型),并根据允许误差大小构建约束函数my_con;③调用fmincon函数对式(6)求解,调用形式为[x,fval]=fmincon(@my_fun,x0,A,b,Aeq,beq,lb,ub,@my_con),其中,x0以所有计算参数均值作为初始值;A和Aeq为不等式约束和等式约束的系数矩阵;b,beq,lb和ub为线性不等式约束的上、下界,在此问题中A,b,Aeq,beq,lb,ub=[]。

图1 可靠指标几何意义示意图
2.2 重力坝可靠指标β的计算方法
本文特根据第2节所述重力坝Kriging模型建立及校验方法,结合重力坝实测资料信息,对不具备实测资料的参数按衰减函数确定其服役后统计信息。在此基础上,结合1.2及1.3节所述方法,建立最佳的Kriging模型拟合重力坝的极限状态方程,根据式(6)构建重力坝可靠指标优化模型,对重力坝的可靠性进行分析计算。
重力坝可靠指标的具体计算步骤如下:
Step1:根据重力坝基本资料确定参数统计信息,抽样获取3 000个样本点组成总样本点集U;
Step2:随机选取40个样本点形成子样本集C1,利用有限元ABAQUS建立重力坝模型进行结构分析,获得各样本点处的结构响应(应力);
Step3:依据应力计算成果,结合式(2)和(3)分别计算重力坝坝体单元强度响应值及抗滑稳定响应值;
Step4:根据样本点的响应值,利用MATLAB对其进行拟合得到近似极限状态方程y=g(x),并根据1.3节所述检验方法判断其是否满足要求,符合精度要求则采用此y=g(x)作为极限状态方程,否则返回Step2;
Step5:基于拟合所得近似极限状态方程y=g(x),根据2.1节所述方法计算重力坝单元强度破坏和抗滑稳定的可靠指标。
3 工程应用
3.1 工程资料及模型建立
某混凝土重力坝总坝长308.50 m,从左岸至右岸共6个坝段,本文选取4#非溢流坝段作为研究对象。根据工程地质勘测资料,该混凝土重力坝所处基岩主要为微风化状态,未勘测出深层的裂缝分布。因此,本文重点基于本文方法分析4#坝段的单元强度破坏和沿建基面滑动失稳的可靠性。该坝段全长50.00 m,坝顶高程179.00 m,最大坝高96.00 m,最小坝高56.00 m,正常蓄水位173.00 m。根据该坝段实际情况,本文利用ABAQUS进行建立有限元模型,其中,基岩尺寸为坝踵和坝趾分别向外延伸1.5倍最大坝高,坝基深度取100.00 m。4#坝段三维有限元模型如图2所示。其中,该模型总节点数27 679个、总单元数23 534个。
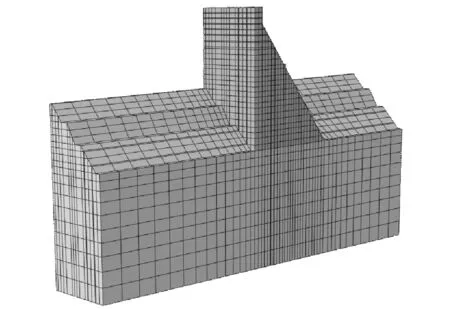
图2 4#坝段网格划分图
3.2 坝体和坝基参数的确定
重力坝大多参数是建坝期间所实测的,重力坝服役多年后其结构参数必将发生演化改变。据此,本文考虑材料参数的老化衰减的影响,对现阶段实测数据不足的参数,根据这些参数的设计标准值和经验衰减函数计算其现在确定值。坝体密度和扬压力衰减函数分别为φ1=e-0.000 5 t和φα=e0.005 t(t为大坝服役年数,下同);混凝土和坝基的弹性模量、抗压强度、抗拉强度、摩擦系数和粘聚力的衰减函数均为φ2=e-0.005 t。同时根据重力坝物理与力学参数变异性对其可靠性计算结果影响大小,影响较小的参数视为定值考虑,而影响较大的参数视为不确定变量,其定值参数统计见表1,不确定参数界限见表2。材料力学模型采用D-P准则。计算施加的荷载组合为:自重+上游水压力+扬压力。
3.3 重力坝可靠指标计算结果
为直观分析重力坝的可靠状态,特根据2.2节计算步骤计算该坝段单元可靠指标β。坝体单元指标分布云图如图3所示,坝体抗滑面和岩基抗滑面单元指标分布云图分别如图4(a)、(b)所示,以及抗滑面单元可靠指标统计如图5所示。根据GB50199—2013《水利水电结构可靠度设计统一标准》相关规定,对于Ⅰ级水利枢纽可靠指标需满足4.2以上。由图3可知,坝体大部分单元可靠指标处于5以上,仅在坝踵附近出现少量的可靠指标较小的单元,不足以威胁大坝正常运行,其中最小可靠指标为2.79,位于坝踵处7 113号单元。再由图4可知,抗滑面也仅在靠近坝踵区域单元可靠指标相对较小,靠近上游单元可靠指标较下游单元大。结合图5可知,坝体和岩基抗滑面共6个单元可靠指标小于4,占总滑面单元(734个)0.8%,该坝段沿建基面抗滑稳定可靠度亦较安全。该重力坝实际运行良好,暂未发现影响大坝正常运行的安全隐患,这也为本文方法计算结果提供了一定的保障。

表1 定值参数统计
注:坝体密度初始设计值2 450,衰减系数0.991 8;扬压力初始设计值0.30,衰减系数1.088 4。

表2 不确定参数界限
注:该坝已服役17年,由衰减函数得衰减系数为0.918 5。
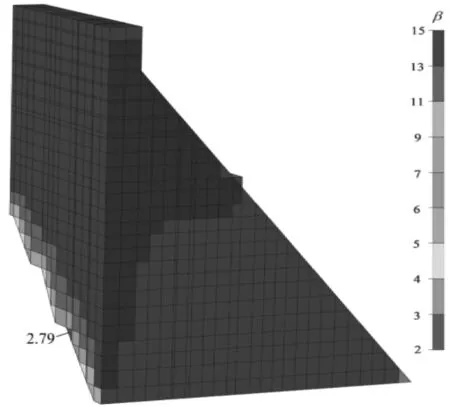
图3 坝体单元可靠指标β分布
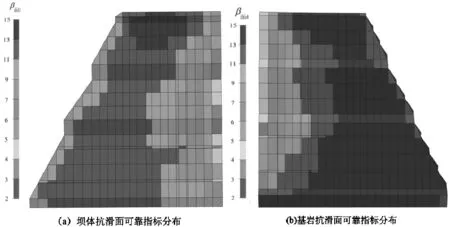
图4 岩基单元可靠指标指标β分布
4 结 论
(1)考虑到重力坝概率可靠性分析时其参数实时获取难特点,本文基于参数的衰减函数获取重力坝服役后的参数统计信息,可更加真实反映重力坝的可靠状态。
(2)本文基于Kriging模型通过合理选取并确定参数概率分布信息,拟合并校验得到最佳极限状态方程以代替重力坝极限状态方程,有效地适应了重力坝极限状态方程高度非线性甚至非显式表达的特点。

图5 抗滑面单元可靠指标指标β统计
(3)本文将重力坝可靠指标求解问题转化为优化问题,构建了重力坝可靠指标优化模型,实现了重力坝所有单元强度破坏及沿坝基面抗滑稳定可靠指标高效计算,为深入分析重力坝可靠状态提供了依据。
