基于多源水文地质信息综合分析模型的应用研究
2019-01-07林利森唐林波
林利森,唐林波
(1.江西省水投建设集团有限公司,江西 南昌 330096;2.江西省水利厅工程建设稽察事务中心,江西 南昌 330009)
我国水资源蕴含量丰富,但人均水资源占有量仅为世界人均占有量的1/4,这就要求我们合理开发和利用水资源。目前,水资源的开发利用存在许多弊端和不足,这不仅降低了水资源的利用率,也极大制约了当地社会经济的发展[1-4]。因此,对于地下水的合理勘测和开采,不仅能够解决水资源短缺的问题,也能在一定程度上解决地下水开采不合理与供水失败情况的出现。
勘测开发利用地下水的最重要前提是要对该地区的水文地质信息进行准确的分析和判断[5-7],但水文地质信息不是单一的要素信息,而是与地层复杂的空间分布、地下水赋存状态与运行规律、地形变化等因素相关的综合信息要素,因此,需要从多角度综合分析地下水的运行规律,才能达到对地下水的合理开发利用,因此,建立相应的多源水文地质信息综合分析模型,对于水资源的准确合理开发具有重要意义[8,9]。
本文在前人研究的基础上,采用层次分析法、嫡值法以及加权算术平均法等理论分析手段[10],建立起基于多源水文地质信息的地下水勘测综合分析模型,对于水资源的精确勘测和合理利用具有重要的现实意义。
1 模型构建
1.1 指标体系的建立
地下水的准确勘测,需要对地下水的赋存、分布和运移规律进行了解和掌握,故此必须建立起一个统一的指标体系,以便较为准确地勘测和利用地下水。寻找地下水,首先需要寻找蓄水构造,这其中包括地层岩性、地质构造和构造的汇水面积等;其次是地形分析,不同的地质形态,会孕育不同的地下水形成和分布规律;然后是地下水流向,包括补给、排泄区与透水层、隔水层的相互关系;再次,则是地下水位的影响,需要勘测了解清楚蓄水构造是位于水位线的上部、中部还是下部;最后则是了解水质的影响,这是判断勘测结构是否适用的基本因素。蓄水构造、地形、地下水流向、水位以及水质等构成了体系的一级指标,而在各个一级指标下又存在着多个二级指标,遵循科学性、动静结合、定量定性互补、实用性及目标导向性等原则,从而可建立起相应的地下水勘测指标体系,见表1。
指标因子赋值原则。蓄水构造:(1)地层赋值。强透水性取0.6~1.0,透水性一般或弱透水性取0.2~0.6;不透水岩层取值小于0.2;(2)地质构造赋值。含张裂破碎带取0.7~1.0,一般断层破碎带取0.3~0.7,无破碎带等区域取值小于0.3;(3)汇水面积赋值。大于20 km2时,取0.7~1,0;5~20 km2时,取0.3~0.7;小于5 km2时,取值小于0.4。若补给区为透水层,排泄区为隔水层,则取0.6~1.0,若补给区为透水层,排泄区为透水层,则取0.2~0.6,若补给区为隔水层,则取值小于0.2。当蓄水构造全部位于水位线以下时,取值控制在0.7~1.0,当蓄水构造部分位于水位线以下时,取值为0.2~0.7,当蓄水构造全部位于水位线以上时,则取值为小于0.2。
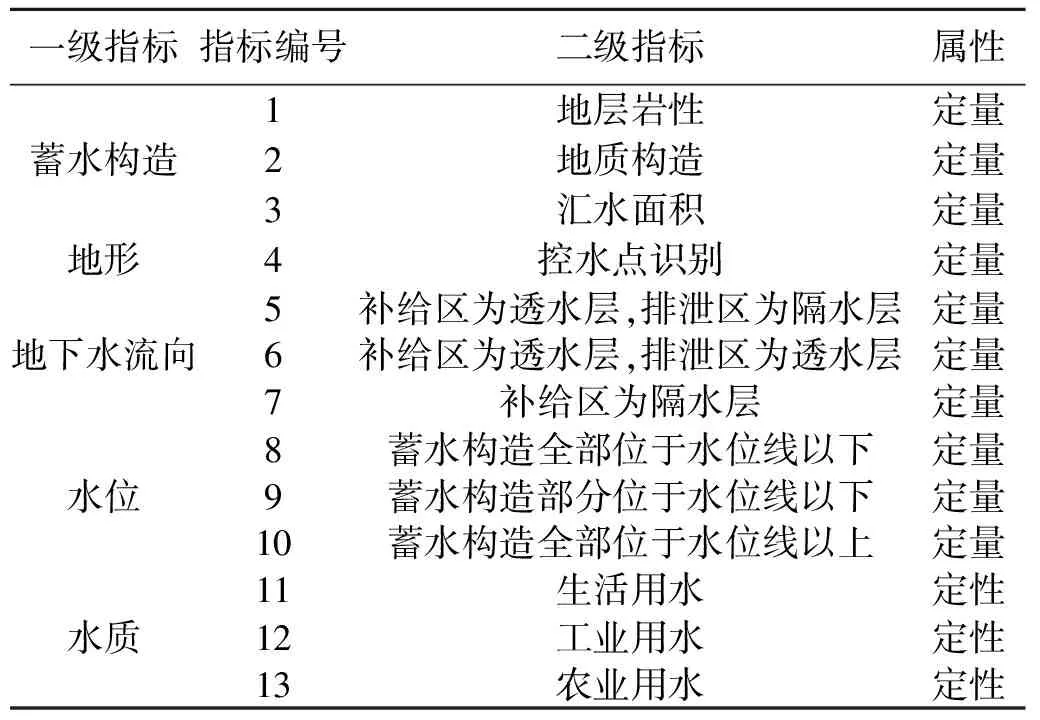
表1 地下水勘测指标体系
1.2 指标因子赋权
层次分析法是一种简单实用的定性与定量相结合的多源信息分析方法,通过建立递阶层次模型和构造出所有的判断矩阵,再通过单排序和总排序的一致性检验,即可分析得到相应指标的权重。嫡值法是不确定信息的一种度量,嫡值越大,指标的离散程度越大,表明该指标对综合评价的影响也越大,但所表示的指标权重越小。利用层次分析法来计算指标的主观权重大小W1(i),利用嫡值法来计算所有指标的客观权重W2(i),即可得到指标的综合权重W(i)。那么根据最小相对信息嫡原理可以得到:
(1)
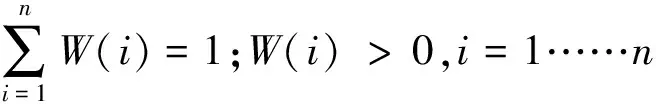
式中:W(i)表示权值,n表示元素个数,i表示指标。那么,利用拉格朗日乘子法即可优化计算得到上述公式:
(2)
上式表明,当取几何平均数时,计算所需的信息量最小,当取其它形式的组合权重时,那么就需要增加大量的其它实际上没有获得的信息。
1.3 综合分析模型
综合分析模型的构建,通常有两种方法:一种是加法合成,另一种则是乘法合成。加法合成的基本式为:
(3)
式中:xi表示指标值,k表示幂次。当k=1时,上式即变为加权算术平均合成模型:
I=W1x1+W2x2+W3x3+……+Wnxn
(4)
根据地下水勘测要求和经验,判断蓄水构造在多源地质信息情况下即多重指标的综合影响下的关键在于蓄水的高低程度是否满足要求,那么就可以利用加权算术平均合成模型,同时根据富水程度指数的大小来统一表示蓄水构造总程度的高低大小,即有:
(5)
式中:i表示蓄水构造区;j表示勘测指标;W(i)表示指标的权重;Fij表示含水程度,其值大于0,小于1;Zi表示富水程度指数,其值大于0,小于1。
2 模型实例论证
2.1 论证区概况
论证区位于江西省某缺水地区,每年实际供水约为154 008 m3,缺水量达108 000 m3/a[11]。由于受到强烈的地质构造活动的影响,本地区的蓄水构造十分复杂,地下水的赋存状态和运行规律不显著,地质剖面示意图见图1。假如仅以某一单要素地质信息来勘测判断该地的地下水情况,可能会存在较大的误差和难度,因此,需要从各方面因素入手,综合考虑多源水文地质信息,才能达到预期的勘测效果。

图1 论证区地质剖面示意图
2.2 论证结果分析
采用论证区1∶5万的地质图、剖面图以及地形地貌图等数据进行模型的分析论证。根据层次分析法和嫡值法计算结果,分别得到了一级指标和二级指标的权重计算结果,见表2和表3。从表中可以看出,一级指标和二级指标的权重值均小于1,满足计算要求,一级指标和二级指标的CR值均<0.1,表明模型计算满足一致性的要求;再通过综合分析模型,对可能的蓄水构造进行判断,推测其富水程度:通过式(1)计算得到单指标影响下的含水程度,再将计算结果代入(5)式,即可分析得到论证区的富水程度。经计算,论证区的Zi值等于0.43,对比富水程度等级指标(见图2)可以看出,论证区的富水程度一般,需要在地下水勘测时选择最佳“宜井位置”,通过控水点的赋值识别,如果有控水点刚好位于富水区,那么该区域则适宜作为采水位置,即可成为宜井的最佳位置,通过识别计算最终选取的宜井位置见图3。
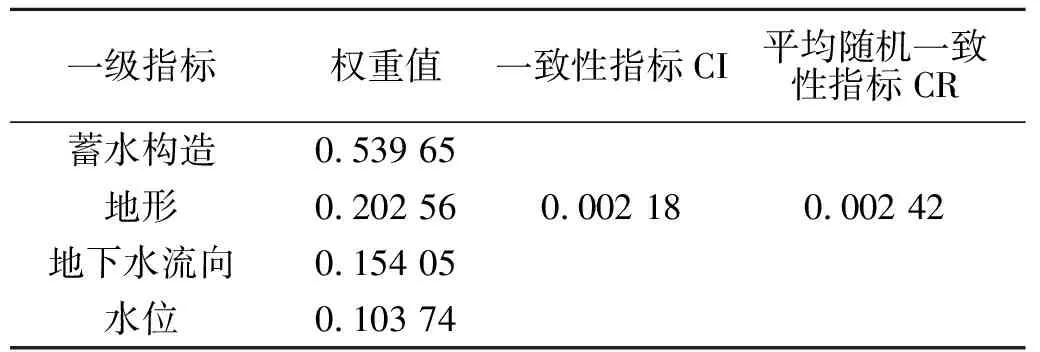
表2 一级指标权重值
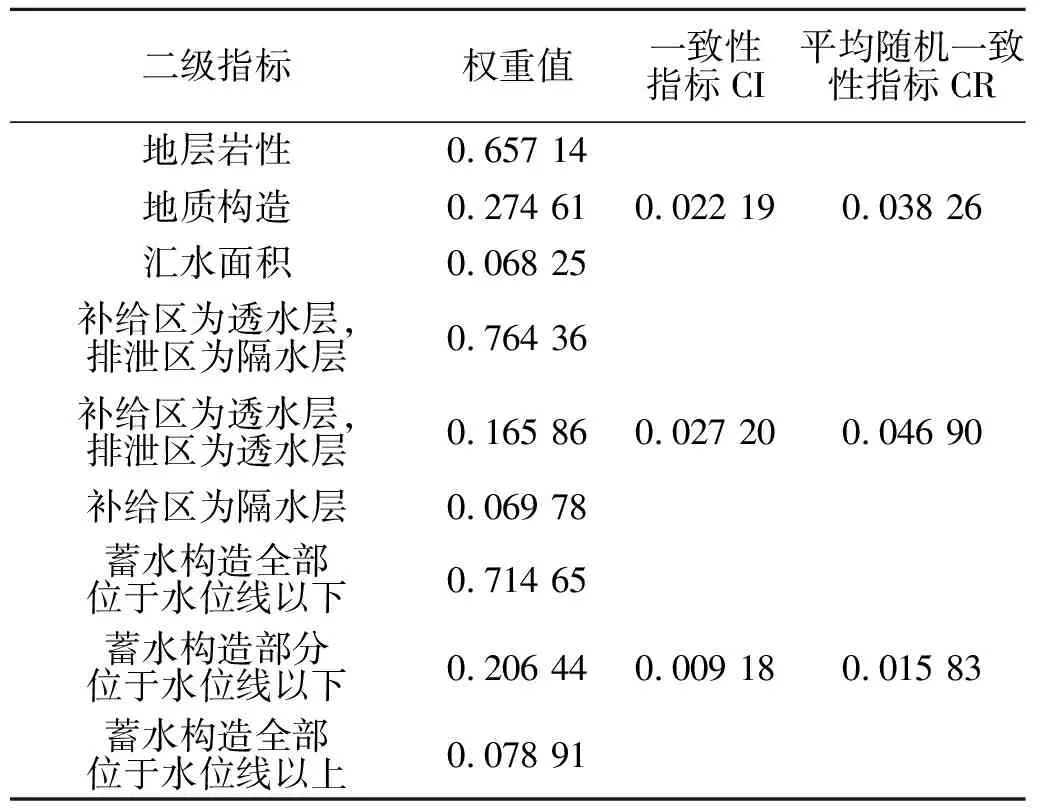
表3 二级指标权重值
3 结 论
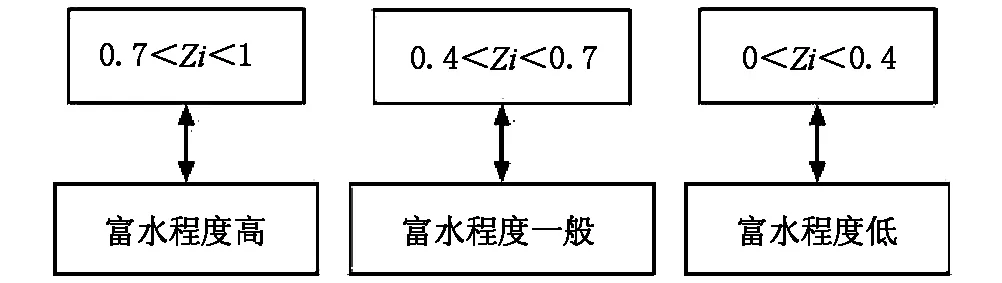
图2 富水程度等级示意图
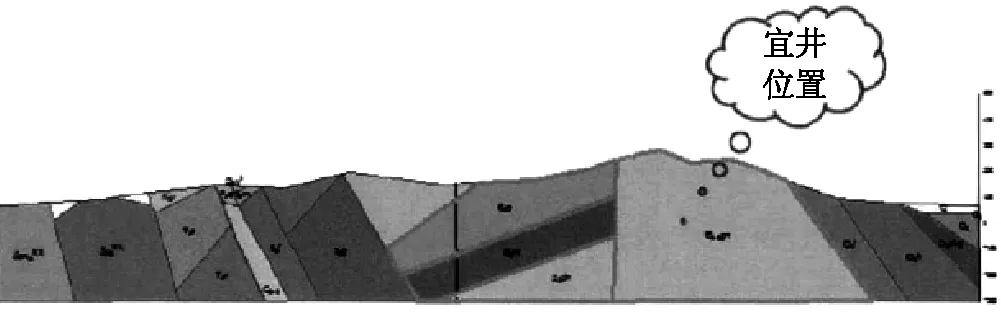
图3 论证区宜井位置
本文针对复杂蓄水构造区地下水勘测难度大的问题,以层次分析法和嫡值法等为理论基础,选用加权算术平均法建立起基于多源水文地质信息的地下水勘测综合分析模型,来对蓄水地区的富水程度进行判断,并进行了实例论证,对实现地下水的精确勘测具有一定的现实意义。
