傅里叶光谱仪光程扫描的鲁棒H∞控制设计
2019-01-07粘伟刘兆军林喆
粘伟 刘兆军 林喆
傅里叶光谱仪光程扫描的鲁棒H∞控制设计
粘伟1,3刘兆军2林喆1,3
(1 北京空间机电研究所,北京 100094)(2 北京空间飞行器总体设计部,北京 100094)(3 先进光学遥感技术北京市重点实验室,北京 100094)
为满足星载时间调制型傅里叶光谱仪光程扫描速度稳定性要求,针对星载光谱仪精密扫描跟踪系统的特点,提出一种鲁棒H无穷(H∞)控制器设计方案。文章首先分析建立了光程扫描系统的数学模型;在此基础上,为达到控制性能要求和鲁棒性要求,采用H∞混合灵敏度的设计方法,阐述了鲁棒H∞控制器设计中加权函数的选择依据和确定过程,利用Matlab鲁棒控制工具箱得到H∞最优控制器。考虑卫星平台振动的影响,建立干扰源模型,对外界干扰的影响进行了仿真验证。仿真结果表明,所设计的鲁棒H∞最优控制器具有良好的扫描跟踪特性,对外界干扰具有良好的鲁棒性,达到了星载光谱仪对高信噪比、高光谱分辨率的光谱探测性能要求。
H无穷控制 鲁棒性光程扫描 干扰模型 光谱探测 航天遥感
0 引言
用于分析大气化学成分变化的星载傅里叶变换光谱仪,它通过对被测光束进行时间或空间调制获取干涉图信号,并对干涉图信号反演获取被测光谱信息[1],因此必须具有高信噪比、高光谱分辨率才能完成对探测光谱的准确反演。
在时间调制型傅里叶光谱仪中,系统需要控制反射角镜往复精密摆动,完成干涉光程差的均匀扫描调制[2]。由于星载仪器受微振动等外界不确定因素干扰的影响,对扫描控制鲁棒性也有较高要求。相关文献分析了动镜倾斜误差及微振动对星载傅里叶光谱仪的影响[3],给出了光谱仪能够承受微振动的临界值[4-5]。同时为保证等光程差扫描采样,相关文献提出了基于ISE的控制器参数优化方法,实现了高精度的干涉光程扫描[6];分析了光谱探测性能对光程扫描控制性能要求间的关系,给出了一种基于极点匹配的控制器设计方法。文献[7]是借助于状态反馈设计结果,同时采用易于工程应用的前项和前馈环节加以有效实现,简化了控制器的设计与实现难度,达到速度稳定度要求。但相应的控制系统设计并未考虑鲁棒性要求。
本文针对某星载傅里叶变换光谱仪,分析建立了挠性支撑的光程扫描系统状态空间模型。根据给出的控制性能要求,基于鲁棒H∞控制理论,采用H∞混合灵敏度设计方法进行控制器设计,详细地给出了加权函数的选择依据和确定过程,最终通过鲁棒控制工具箱得到H∞最优控制器。考虑实际工作过程中卫星平台振动的影响,建立了干扰源模型,分析了系统对外界干扰的鲁棒性,通过仿真验证了本文设计方法具有良好的位置跟踪性能且对外界扰动有较强的鲁棒性。
1 光程扫描系统模型
本星载傅里叶变换光谱仪系统采用带挠性枢轴的音圈电机作为扫描的执行器件。电机与摆臂之间采用挠性枢轴连接,可以有效克服轴承连接带来的摩擦力矩的影响,但由于挠性枢轴的引入使系统为变负载运动,因此增加了控制系统研制难度。光谱仪应用摆臂上对称固定的角镜来完成光程差调制,加上端镜作用,使得整个光路的最大光程与机械行程之间形成了8∶1的关系。这种折叠式光路大大减少了动镜移动距离,满足对星载仪器体积的要求,可在较小空间内实现大的光程差扫描[8]。为达到扫描精度要求,采用共光路的激光计量系统提供采样脉冲和位置反馈脉冲[9]。
光谱仪光路图如图1(a)所示。如图1(b),位置为摆臂起始运动位置,光线垂直摆臂,对应干涉仪零光程差。和位置摆臂运动过程中将到达位置。假设摆臂逆时针转动角度到达位置,为时间变量的函数,则光程差(Optical Pass Difference,OPD),即线段OM为:

式中b为摆臂长度。由光谱探测基础理论可知,光谱分辨率v与光程差OPD之间满足关系:

一般来说,要对大气层中的主要气体组分进行有效识别,仪器的光谱分辨率要达到0.02cm–1水平[10]。因此,由式(2)可得需要的光程差为25cm。当达到最大光程差时,由式(1)可以计算得到最大摆角约为±13.38°。因此,尽管干涉仪的光学结构采用了折叠设计方案,摆臂机构仍然要有较大摆角,并且摆臂的摆动角度与干涉仪的光程差速度是非线性的关系,这也增加了摆臂扫描控制系统研制的难度。
光程扫描过程中,电机的电压方程和运动方程如下:
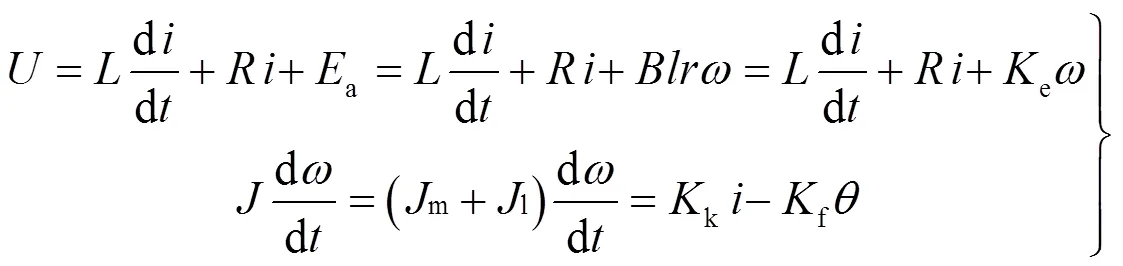

图2 系统状态空间图

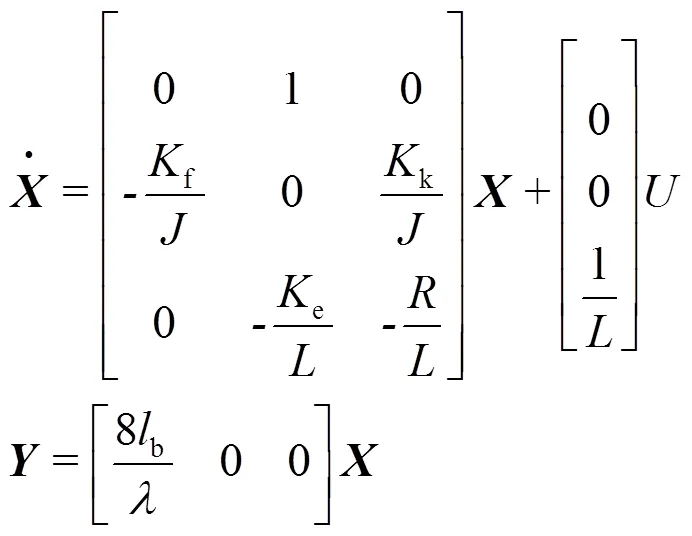
可得到扫描系统的系统矩阵,控制矩阵,输出矩阵和直接传递矩阵分别为:


对上述传递函数,通常选择经典控制论进行控制器设计,如PID控制、极点匹配控制。但以上控制方法均是在未考虑卫星平台振动带来的不确定性因素影响下进行系统的运动控制,即:使控制性能满足要求,鲁棒性却难以达到要求。为此,本文采用鲁棒H∞控制器进行控制系统设计,以期达到要求。
2 鲁棒H∞控制器设计
2.1 加权的控制结构

针对外部干扰和模型的不确定性,H∞控制器的设计可以归结为混合灵敏度问题[13],即:寻找真实有理函数控制器K使闭环系统稳定,且满足范数要求。由于H∞控制器的阶次等于被控对象和权函数阶次之和,所以要尽可能选阶次较低的加权函数[14]。
将干涉仪干扰力矩从被控对象中移出,加载到系统输出端,转换为对编码个数影响的不确定性,得到如下控制系统结构图。图4中各参量定义与图3相同。

图3 一般加权灵敏度函数

图4 控制系统结构
2.2 加权函数的选择方法
为了选择合适的加权函数,首先对扫描指令曲线作傅里叶变换,得到被跟踪信号的频谱主要形状及其分布。根据跟踪信号的频谱特性,考虑卫星平台振动的影响,给出满足条件的加权函数。
图5给出了规划曲线频谱图,可以看到,规划曲线频谱中会出现多个谐波分量。

图5 规划曲线频谱图
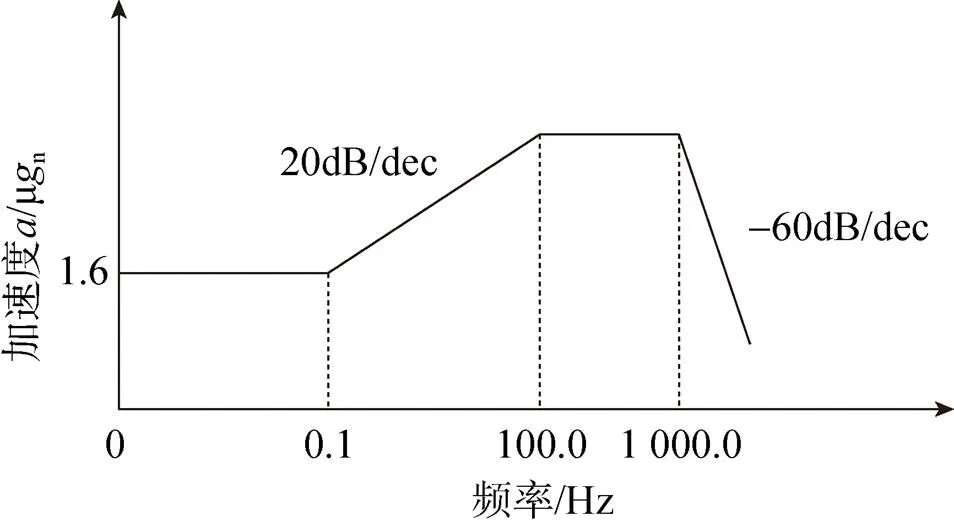
图6 振动加速度幅频特性
由此近似得到振动加速度,
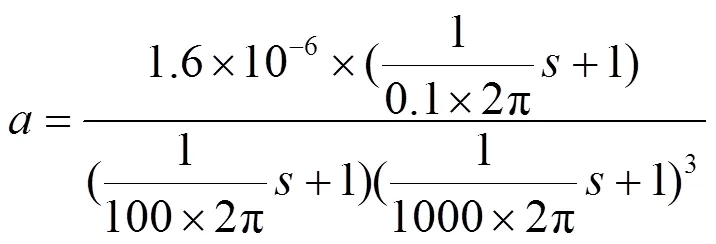
通过振动加速度得到干扰力矩,将干扰力矩按控制系统结构图所示变换为角度值,单独作用于系统输出。考虑摆臂往复运动对光程的8倍放大作用,最终将角度变化转变为激光计量脉冲编码Mq的变化。即

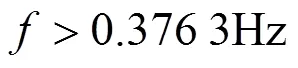

图7 振动频率对编码影响
根据上述分析,考虑以下几点[15]:

综合上述分析,各加权函数选定如下:



根据给定的加权函数,利用鲁棒控制工具箱,由图8得到H∞最优控制器。
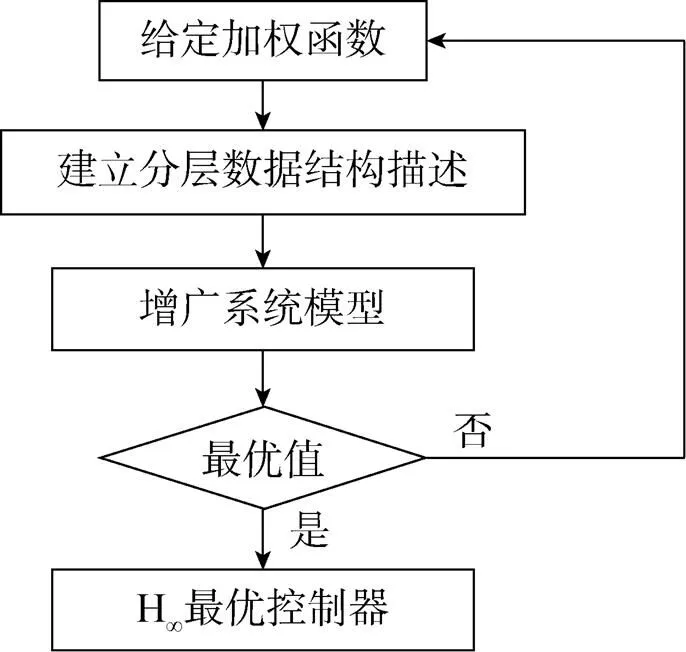
图8 H∞控制器设计流程
经反复迭代计算,提取控制器系统状态方程模型,得到的控制器零极点方程为:

根据上述H∞控制器,对摆臂运动控制系统的速度稳定度仿真分析,对匀速段和调头段放大处理,得到结果如图9所示。通过数据分析可知,速度稳定度严格满足控制指标要求,且换向冲击小,调头时间足够小。
3 干扰源的建立与鲁棒性仿真
如图6所示,根据卫星平台振动加速度幅频特性,得到式(7),进而根据干扰力矩与振动加速度的关系得到干扰力矩的频谱特性。以高斯白噪声作为输入[16],通过振动加速度传递函数构造干扰源模型。将10s内的输出数据保存,通过Matlab仿真分析,得到干扰源频谱特性如图10所示。可以看到,干扰源的频谱特性符合卫星平台振动加速度幅频特性。可以将此作为对干涉仪运行过程中外界的不确定性干扰,从而验证控制器的鲁棒稳定性[17-18]。
在Simulink仿真工具箱中,将外界干扰加入基于H∞的控制方法中,观察位置跟踪曲线与速度曲线的变化,并将采样速度值以向量的形式导出,方便后续数据处理。根据所得数据,在Matlab软件中仿真得到存在外界干扰的情况下的速度曲线。截取匀速运动段分析比较可以得到,基于鲁棒H∞的控制方法能满足速度稳定度大于99%的要求,且具有良好的鲁棒性。图11给出的是本系统两种控制方法得到的速度曲线放大图,通过比较可以很清楚的看到H∞控制器具有更好的鲁棒性。

图10 干扰源功率谱密度
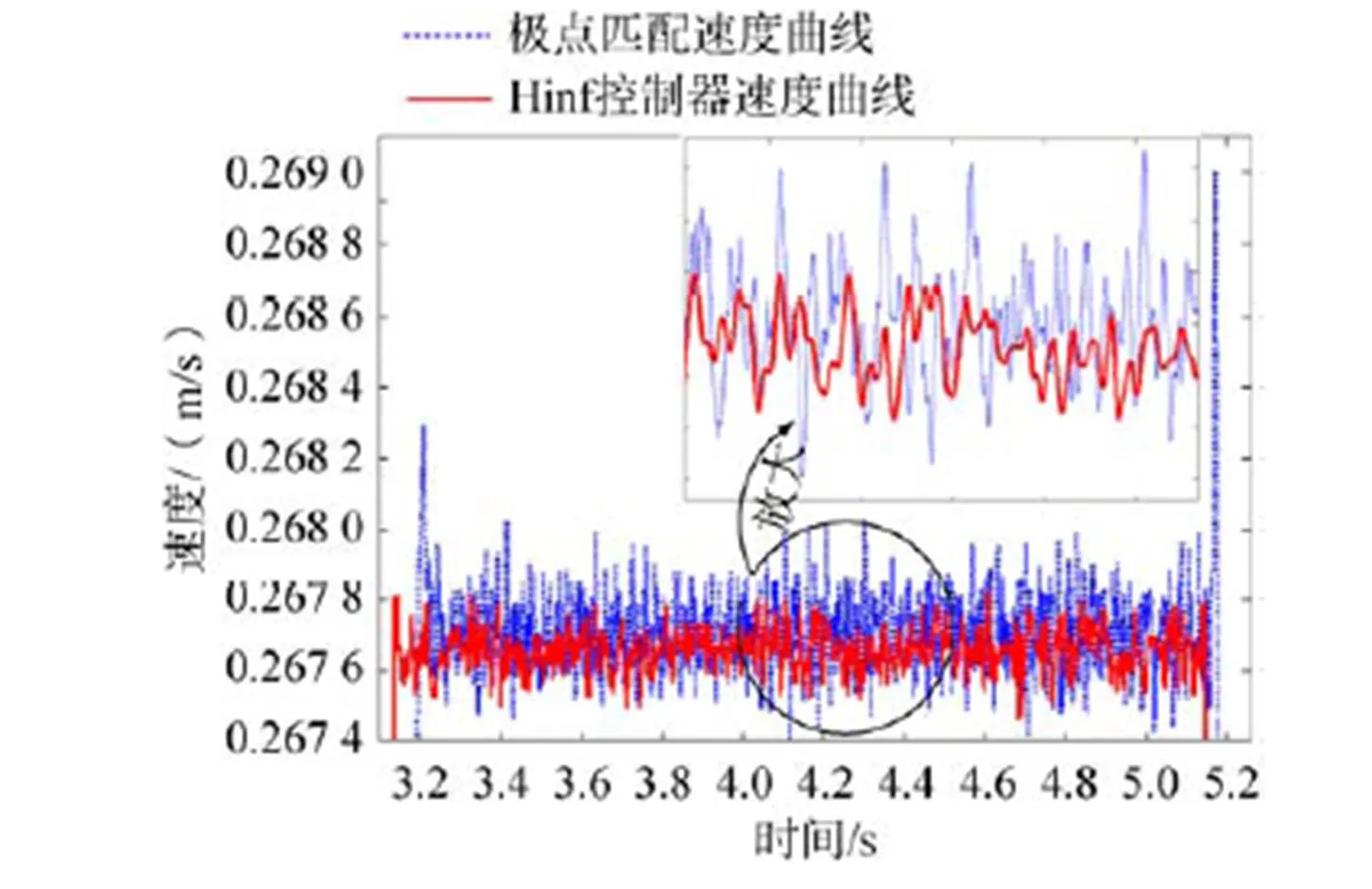
图11 速度曲线比较
4 结束语
高分辨率光谱探测对星载干涉仪的光程扫描系统及其鲁棒性有极其严苛的要求,光程扫描速度波动稳定性直接决定了干涉图到光谱图的等效转换。本文设计了鲁棒H∞控制器,考虑了仪器工作过程中受卫星平台振动等不确定性影响,建立了干扰源模型,并进一步分析了系统鲁棒性,仿真结果表明本文的鲁棒H∞控制器对位置跟踪性能及光程差速度稳定性均优于极点匹配PID控制方法,最终确定了该方法在扫描控制中的有效性。该结论对星载干涉仪的光程扫描系统的控制器设计与工程实现具有重要的参考价值。
[1] 张淳民. 干涉成像光谱技术[M]. 北京: 科学出版社, 2010. ZHANG Chunmin. Interference Imaging Spectrometer Technology[M]. Beijing: Science Press, 2010. (in Chinese)
[2] COMOLLI L, SAGGINA B. Analysis of Disturbances in the Planetary Fourier Spectrometer through Numerical Modeling[J]. Planetary and Space Science, 2010, 58: 864-874.
[3] 曾立波, 尹邦胜, 何冰, 等. 傅立叶变换红外光谱仪动镜倾斜误差分析[J]. 光学精密工程, 2006, 14(2): 191-196. ZENG Libo, YIN Bangsheng, HE Bing, et al. Error Analysis of Moving Mirror in Fourier Transform Interferometer[J]. Optics and Precision Engineering, 2006, 14(2): 191-196. (in Chinese)
[4] 范东栋, 白绍竣. 微振动对星载傅里叶变换光谱仪的影响分析[J]. 航天返回与遥感, 2013, 34(4): 59-65. FAN Dongdong, BAI Shaojun. Influence of Micro-vibration on Space-borne Fourier Transform Spectrometer[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(4): 59-65. (in Chinese)
[5] 段鹏飞, 李明, 徐彭梅. 微振动对干涉仪运动机构均匀性的影响分析[J]. 航天返回与遥感, 2013, 34(6): 44-50. DUAN Pengfei, LI Ming, XU Pengmei. Influence on Velocity Uniformity of Interferometer Mechanism of Micro-vibration[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(6): 44-50. (in Chinese)
[6] 粘伟, 刘兆军, 林喆, 等. 迈尔尔逊干涉仪的摆臂扫描控制[J]. 科学技术与工程, 2012, 12(33): 8859-8865. NIAN Wei, LIU Zhaojun, LIN Zhe, et al. Arm Scanning Control of Michelson Interferometer[J]. Science Technology and Egineering, 2012, 12(33): 8859-8865. (in Chinese)
[7] 粘伟, 刘兆军, 林喆, 等. 傅里叶光谱仪的光程扫描控制系统设计[J]. 红外与激光工程, 2013, 42(8): 2085-2091. NIAN Wei, LIU Zhaojun, LIN Zhe, et al. Optical Path Scanning Control System Design of the Fourier Spectrometer[J]. Infrared and Laser Engineering, 2013, 42(8): 2085-2091. (in Chinese)
[8] MARC-ANDRE S, FRANCOIS C, CHRISTOPHE D, et al. ACE-FTS Instrument Detailed Design[J]. SPIE, 2002, 4814: 176-188.
[9] 管恩义, 王平, 范东栋, 等. B3M傅里叶变换红外光谱仪干涉图采样触发信号的误差研究[J]. 光学技术, 2009, 35(s): 74-76. GUAN Enyi, WANG Ping, FAN Dongdong, et al. B3M Infrared Fourier Transform Spectrometer Sampling Pulse Error Research[J]. Optical Technique, 2009, 35(s): 74-76. (in Chinese)
[10] 巫晓丽, 范东栋, 王平. 空间大气成分探测傅里叶变换红外光谱仪[J]. 航天返回与遥感, 2007, 28(2): 15-20. WU Xiaoli, FAN Dongdong, WANG Ping. Fourier-transform Infrared Spectrometer for Space Atmospheric Component Detecting[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(2): 15-20. (in Chinese)
[11] 刘豹, 唐万生, 著. 现代控制理论[M]. 北京: 机械工业出版社, 2006. LIU Bao, TANG Wansheng. Modern Control Theory[M]. Beijing: Machinery Industry Press, 2006. (in Chinese)
[12] 王广雄, 李连峰, 王新生. 鲁棒设计中参数不确定性的描述[J]. 电机与控制学报, 2001, 5(1): 5-7. WANG Guangxiong, LI Lianfeng, WANG Xinsheng. The Description of the Parameter Uncertainty for Robust Design[J]. Electric Machines and Control, 2001, 5(1): 5-7. (in Chinese)
[13] 俞立. 鲁棒控制-线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002: 41-44. YU Li. Robust Control—LMI Processing Methods[M]. Beijing: Tsinghua University Press, 2002: 41-44. (in Chinese)
[14] 高云霞, 田沛, 李沁. H∞控制理论在主汽温控制系统中的应用[J]. 电力科学与工程, 2005(3): 25-27. GAO Yunxia, TIAN Pei, LI Qin. Application of H∞Control Theory to Main Stream Temperature Control Systems[J]. Electric Power Science and Engineering, 2005(3): 25-27. (in Chinese)
[15] 刘彦文, 刘胜, 王毅. 船舶舵减摇的控制设计[J]. 电机与控制学报, 2009, 13(1): 133-137. LIU Yanweng, LIU Sheng, WANG Yi. H∞Design for Rudder Roll Stabilization of Ships[J]. Electric Machines and Control, 2009, 13(1): 133-137. (in Chinese)
[16] HAN Q. Robust Stability of Uncertain Delay-differential Systems of Neutral Type[J]. Automatics, 2002, 3(8): 719-723.
[17] 张俊红, 于镒隆, 高宏阁. 汽轮机轴系弯振干扰抑止问题鲁棒H∞控制[J]. 振动工程学报, 2006, 19(1): 118-123. ZHANG Junhong, YU Yilong, GAO Hongge. Bending Vibration Control of a Turbo-generator Shaft with Disturb Based on Robust Method[J]. Journal of Vibration Engineering, 2006, 19(1): 118-123. (in Chinese)
[18] 李会军, 陈明军. 基于LMI的H∞鲁棒PID控制器设计[J]. 控制工程, 2007, 14(3): 294-296. LI Huijun, CHEN Mingjun. Design of H∞Robust PID Controller Based on LMI[J]. Control Engineering of China, 2007, 14(3): 294-296. (in Chinese)
Optical Path Scanning Design Based on Robust H∞Control for the Fourier Spectrometer
NIAN Wei1,3LIU Zhaojun2LIN Zhe1,3
(1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)(2 Beijing Institute of Spacecraft System Engineering, Beijing 100094, China)(3 Beijing Key Laboratory of Advanced Optical Remote Sensing Technology, Beijing 100094, China)
To reach the speed stability requirements of the spaceborne time modulated Fourier spectrometer, the design scheme based on H∞robust control is proposed in view of the precise scanning and tracking of the spaceborne spectrometer. Firstly, the mathematical model of the scanning system is analyzed and then established. Secondly, the H∞hybrid sensitivity design method is used to achieve the control performance requirements. In the meantime, the selection criteria of the weighting function are explained and then the H∞optimal controller is obtained using the MATLAB robust control toolbox. Considering the influence of vibration of the satellite platform, the interference source model is established to verify the boundary interference influence. The simulation results show that the designed H∞robust controller has good performance in scanning and tracking as well as good robustness, achieving the requirements of the high signal-to-noise ratio and high spectral resolution in spaceborne spectrometer.
H∞control; robustness; optical path scanning; interference model; spectral detection; space remote sensing
TM301.2;TH744
A
1009-8518(2018)06-0055-09
10.3969/j.issn.1009-8518.2018.06.007
2018-02-23
国家重大科技专项工程
粘伟,男,1987年生,2013年获中国空间技术研究院飞行器设计专业硕士学位,工程师。主要研究方向为空间光学遥感器控制技术研究。E-mail:nianwei1@126.com。
(编辑:庞冰)
