栅格翼在减小火箭残骸落点散布上的应用
2019-01-07贾洪印徐明兴张培红吴晓军和争春
贾洪印 徐明兴 张培红 吴晓军 和争春
栅格翼在减小火箭残骸落点散布上的应用
贾洪印 徐明兴 张培红 吴晓军 和争春
(中国空气动力研究与发展中心计算空气动力研究所,绵阳 621000)
文章利用栅格翼高气动效率、高阻力的特点,探索其在火箭芯一级残骸落点散布控制上的应用。首先介绍了栅格翼气动性能分析采用的数值模拟方法,通过与试验数据对比,验证了方法的可靠性。针对火箭芯一级箭体,开展了栅格翼设计研究,给出了详细的栅格翼几何尺寸,分析了其在亚跨超声速阶段气动性能,通过6自由度蒙特卡罗弹道拉偏仿真,对比了栅格翼安装前后火箭芯一级残骸落点散布范围。结果表明,火箭芯一级加装栅格翼后,上升段折叠安装,阻力增量较小,超声速阶段阻力增量2%以内;再入段栅格翼打开,小迎角范围内火箭芯一级残骸压心后移明显,气动稳定性增强;芯一级残骸进入大气层后飞行姿态迅速振荡收敛,残骸落点散布范围大幅缩小,安装栅格翼后火箭芯一级落点散布面积减小约76%,这种基于稳定栅格翼进行落点控制的方法具有机械结构简单,易于工程实现的特点,适用于各类运载火箭的改造,可大幅度减小落区的范围。
栅格翼 稳定性 落点散布 弹道仿真 火箭 航天回收
0 引言
失稳飞行器,如:飞行器破损产生的残骸、火箭脱落的整流罩和助推级等,通常是不可控的飞行器,坠落到地面时有可能带来安全问题[1]。为了保障这些飞行器的落区安全,可以从两个方面入手[2]:一是将其落点控制在人烟稀少的地方;二是提高落区划定的精度,减小落点散布的范围。由于受到飞行器目标轨道、发射场位置、机动能力、总体设计等方面的限制,这些失稳飞行器的落点难以有效控制到人烟稀少的地方,因此提高落区划定的精度,减小落点散布的范围,对保障落区人员和财产安全,具有十分重要的意义。
运载火箭子级按回收的方式不同,大致可分为伞降回收、带翼飞回式和垂直返回回收三种类型[3]。伞降回收[4]是利用降落伞实现火箭子级的减速过程,通过姿控发动机(Reaction Control System,RCS)或者翼伞来调整姿态,实现火箭子级的回收。美国在伞降方面积累了大量经验,发展了用于航天飞机固体火箭助推器回收系统[5]。伞降回收的典型代表是美国的航天飞机助推器、战神I-X助推器[6]、K-1运载火箭[7]等。带翼飞回式子级回收的主要思想是在传统火箭上添加机翼,利用控制舵面和RCS系统,实现水平着陆,如美国的航天飞机、俄罗斯正在研制的新型运载火箭“安哥拉”[8]。火箭子级垂直回收是火箭子级在完成任务后,通过自身携带的控制系统和动力装置,按照设定的轨迹自主飞回着陆场,并以垂直的箭体姿态缓慢降落到指定着陆场,其典型代表就是美国Space X公司的Falcon 9火箭[9]和蓝色起源公司的New Shepard火箭。相比有翼水平着陆的子级回收方式,垂直返回对火箭外形及总体布局影响较小。在火箭子级垂直返回回收中,涉及多项复杂关键技术[10],如再入大气层热防护技术、先进火箭发动机技术、垂直返回高精度控制技术、高可靠性着陆支撑技术等。Space X公司在Falcon 9火箭垂直返回控制中,采用了栅格舵和RCS复合的再入返回控制方案,实现了助推火箭一子级的精确回收。
栅格翼是一种新型控制稳定面,由多个薄的栅格壁板构成。它作为一种新型升力面和控制面,在亚声速和高超声速阶段有比平板翼更优秀的气动特性,可用作稳定翼或全动式舵翼以提高弹箭的机动性,增加其稳定性和可控性[11]。与传统平板翼相比,栅格翼具有一些独特优点[12-15],在相同的外形尺寸下,栅格翼的升力面积比平板翼大得多;具有较高的强度质量比;栅格翼弦向尺寸小,可以紧贴主体折叠安装,而不增加主体的外形尺寸;在控制效率和铰链力矩特性方面优于传统平板翼。对于炸弹和导弹等飞行器,栅格翼缺点主要是相较于平板翼阻力较大,而对于高速返回的火箭芯一级箭体,这个缺点却成为了优点,可以提供额外的气动阻力,减小火箭芯一级残骸返回速度。
本文借鉴Space-X火箭回收技术,利用栅格翼高气动效率、高阻力的特点,探索栅格翼在火箭芯一级残骸落点散布控制上的应用。本文首先介绍了栅格翼气动性能分析采用的数值模拟方法,通过与试验数据对比,验证了方法的可靠性。针对火箭芯一级箭体,开展了栅格翼设计研究,分析了其在亚跨超声速阶段气动性能,通过6自由度蒙特卡罗弹道拉偏仿真,对比了火箭芯一级残骸安装栅格翼前后飞行姿态变化和落点散布范围的变化。
1 数值分析方法及验证
1.1 数值模拟方法介绍
本文栅格翼气动特性数值模拟分析采用中国空气动力研究与发展中心自主研制的亚跨超声速流场解算器MFlow,该解算器支持任意形状的网格单元,具备大规模并行能力,可用于各种定常、非定常流动问题的模拟,在航空航天领域得到了广泛的应用,软件经过了大量标准算例的考核验证[16-18]。
在本文的研究中,控制方程采用三维非定常可压缩的Navier-Stokes方程,计算网格采用三棱柱和四面体混合的非结构网格单元,主控方程对流项采用目前应用广泛、具有较高间断和黏性分辨率的Roe格式进行离散,黏性项采用中心格式,时间推进采用隐式LU-SGS(Lower Upper Symmetric Gauss-Seidel)方法,线性重构时梯度求解采用节点型Gauss方法。为了加速流场收敛,采用了局部时间步长和FAS(Full Approximation Storage)融合的多重网格技术。在湍流流动模拟方法方面,采用目前工程应用广泛、鲁棒性高的SA(Spalart Allmaras)一方程湍流模型。物面采用无滑移、无穿透、绝热边界条件,远场采用无反射远场边界条件。
1.2 方法验证
在跨声速阶段,栅格翼内存在流动壅塞现象[19],对数值模拟要求较高,为了验证本文数值模拟方法和网格技术的可靠性,以某导弹为研究对象,选取其2×4栅格翼导弹标模外形,对数值模拟方法进行了验证确认。带栅格翼的导弹外形及尺寸如图1(a)所示,栅格翼详细尺寸及三维几何外形如图1(b)所示,图中尺寸以弹体底部直径进行了归一化,为头部曲线对应的圆弧半径。数值模拟采用三棱柱和四面体混合的非结构网格单元,如图2所示,网格总量约为1 500万个,网格第一层间距归一化≈1,在前缘和栅格翼表面等区域,采用各向异性网格技术,栅格翼弦向网格点数35个,格子宽度方向网格点数25个。
图3给出了跨声速阶段马赫数为0.8~1.6范围内全弹零升阻力计算、风洞试验结果[20]和文献参考值[21]的对比曲线。可以看出,数值计算结果与风洞试验结果吻合较好,说明采用的数值计算方法可以较好地预测栅格翼跨声速阶段复杂的流动特性,验证了本文栅格翼气动特性分析方法的可靠性。
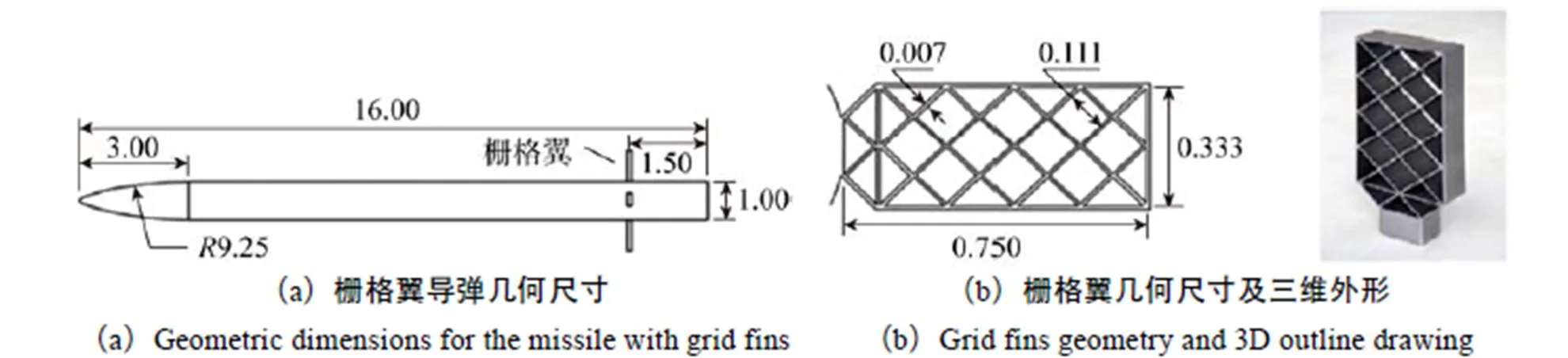
图1 栅格翼标模尺寸
图2 栅格翼截面网格
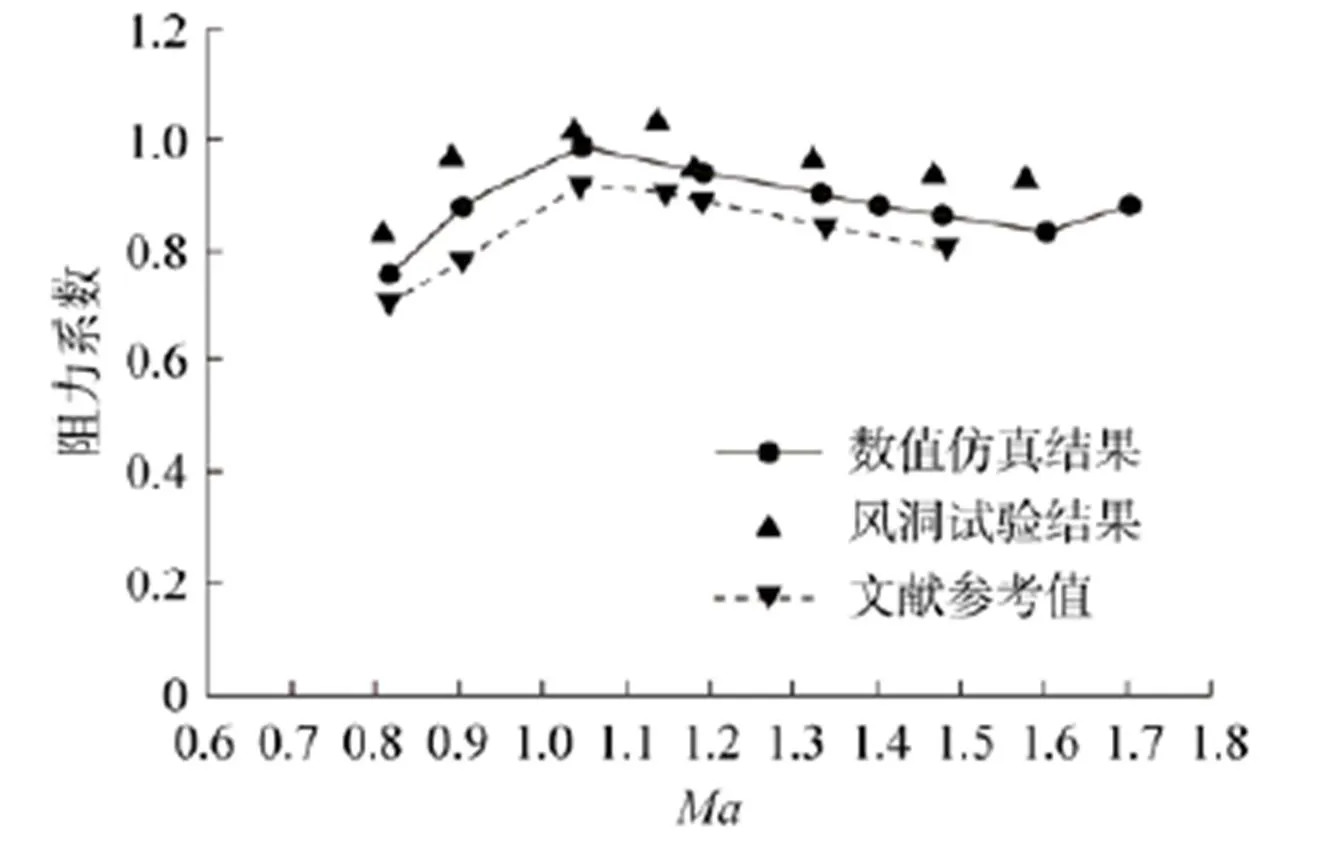
图3 计算与风洞试验对比
2 栅格翼设计及气动性能分析
2.1 栅格翼设计
针对火箭芯一级箭体,开展了栅格翼设计研究,具体设计要求如下:在结构方面,为了减小安装栅格翼对火箭运载能力的影响,要求设计的栅格翼在上升段可折叠安装在火箭芯一级箭体上,栅格翼结构质量尽可能小,结构强度满足全速域使用要求;在气动性能方面,要求上升段对火箭自身气动性能影响较小,高速返回段栅格翼展开后满足气动稳定性要求。
图4给出了设计的栅格翼外形图,栅格翼采用弧形设计,上升段可折叠安装在箭体上,格子数目为6×7,栅格翼外边框尺寸为1 416mm×1 208mm,栅格翼弦长100mm,格宽135mm,格弦比为0.74,格壁厚度为5mm,外框厚度10mm。同时,为了满足折叠安装要求,设计了相应的折叠和转动机构。假设栅格翼材质为实心全钢结构,单片栅格翼的总质量约为150kg。由于本文设计的栅格翼不需要考虑减阻特性,所以栅格翼前缘位置并未倒圆处理。
2.2 气动性能分析
针对设计的栅格翼外形,将其安装在火箭芯一级箭体上,开展了上升段和返回段气动特性数值仿真分析。四片栅格翼呈“X”形布局形式,安装在火箭一、二级连接舱位置,栅格翼展开后的外形如图5所示。
数值模拟采用三棱柱和四面体混合的非结构网格单元,网格总量约为6 800万个,其中三棱柱单元约为4 800万个,四面体单元约为2 000万个,网格第一层间距≈1。图6给出了模拟采用的表面网格和空间网格分布图,可以看出,在栅格翼的表面,采用了各向异性的三角形单元进行模拟,栅格翼弦向网格点数为24个,格子宽度方向网格点数为20个,为了较好的模拟黏性效应,附面层内采用棱柱层进行模拟。同时,在栅格翼附近整个空间区域都进行了加密处理,可以满足栅格翼气动力数值模拟要求。

图4 设计的栅格翼外形

图5 火箭芯一级加装栅格翼外形
气动特性数据分析基于英美坐标系,即轴向前为正,轴向右为正,轴向下为正,参考质心距离火箭底部32%总长度,栅格翼质量相对火箭箭体质量为小量,忽略安装栅格翼对火箭残骸质心的影响。
在上升段,栅格翼折叠安装在火箭箭体上,需要评估增加栅格翼后对火箭上升段气动特性的影响。图7给出了上升段栅格翼折叠后对整个火箭阻力特性的影响曲线,可以看出,栅格翼折叠后对火箭上升段的阻力影响较小,在超声速阶段,火箭阻力增量在2%以内,亚声速时由于火箭总阻力相对较小,阻力增量的百分比略有增大,但最大不超过总阻力的6%。
在再入段,火箭芯一级残骸属于无控飞行器,其飞行迎角、姿态主要由芯一级箭体的气动稳定性决定。图8给出了亚、跨、超声速典型马赫数下0°~180°迎角范围内有无栅格翼火箭芯一级残骸俯仰力矩特性和压心特性的对比曲线。图中俯仰力矩特性曲线力矩参考点为火箭芯一级残骸质心,表示马赫数。可以看出,火箭芯一级残骸增加栅格翼后,在小迎角范围内,压心发生明显的后移,随着迎角的逐渐增大,栅格翼面开始发生流动分离,栅格翼的气动效率降低,压心后移量逐渐减小;在120°迎角以后,由于气流方向的改变,栅格翼的气动效率开始逐渐增强,压心后移量随着迎角的增大而逐渐变大。同时,从俯仰力矩特性曲线可以看出,有无栅格翼外形俯仰力矩随迎角变化的趋势基本一致,其原因是在较大迎角时,栅格翼上产生的俯仰力矩比箭体产生的俯仰力矩小很多,俯仰力矩变化主要由箭体上俯仰力矩变化产生。在小迎角时,箭体自身产生的俯仰力矩量值和栅格翼上的俯仰力矩量值基本相当,从而使得小迎角范围内的稳定性发生了改变。对比不同马赫数下的俯仰力矩特性曲线,可以看出,对于无栅格翼外形,在0°~180°范围内,存在多个俯仰力矩系数为零的平衡点,增加栅格翼后,平衡点个数减小为2个,对应迎角分别为0°和180°,且180°迎角时,俯仰力矩对迎角的导数大于0,为静不稳定平衡点。
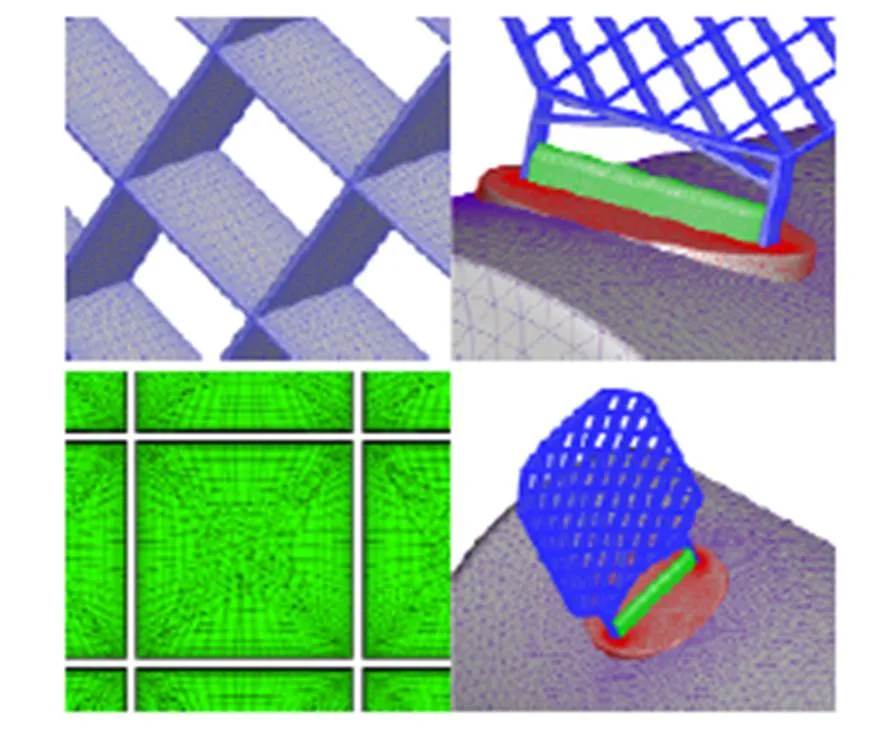
图6 网格分布

图7 上升段阻力特性对比

图8 再入段不同马赫数下气动特性对比
3 火箭芯一级残骸落点散布初步仿真
3.1 基于蒙特卡罗的落点散布分析方法
火箭芯一级残骸再入返回过程中,干扰因素较多,为综合分析相关因素的影响,采用经典的统计学试验方法—蒙特卡罗方法,分析预测落点散布范围。
基于蒙特卡罗的弹道仿真分析方法,其主要步骤为:
1)对影响火箭芯一级落点散布的影响因素进行分析,确定其概率分布,建立干扰因素偏差概率模型;
2)根据各个干扰因素偏差出现的概率进行随机抽样,产生符合干扰变量概率分布规律的抽样值;
3)将干扰因素抽样值代入弹道数学模型进行仿真分析;
4)重复2、3步,建立大量落点散布样本,利用数理统计理论进行统计分析。
概率模型的可靠程度直接影响仿真分析结果,要求所建立的概率模型,能够正确反映各干扰因素的实际情况和概率分布。在本文的火箭芯一级落点散布分析中,考虑了气动力偏差、火箭芯一级质量惯量特性偏差、火箭一二级分离点参数偏差和大气环境偏差影响。
3.2 落点散布仿真结果分析
针对火箭芯一级加装栅格翼后的气动布局方案,开展了残骸落点散布的仿真分析,分析了无控栅格翼对火箭芯一级残骸再入姿态和落点散布范围的影响,每种方案进行了10 000条弹道的蒙特卡罗拉偏仿真。
图9给出了火箭芯一级残骸加装栅格翼进入大气层后基准弹道仿真曲线。可以看出,火箭上升段一二级分离后,芯一级残骸由于惯性会继续向前飞行,到达一定高度后,由于地球引力作用,开始向大气层再入。火箭芯一级残骸进入大气层后,飞行姿态振荡收敛,最终落地迎角在0°附近,与之前气动性能分析结果相一致。在大气层内,火箭芯一级残骸由于气动阻力作用,马赫数逐渐降低,落地时马赫数约为0.4。
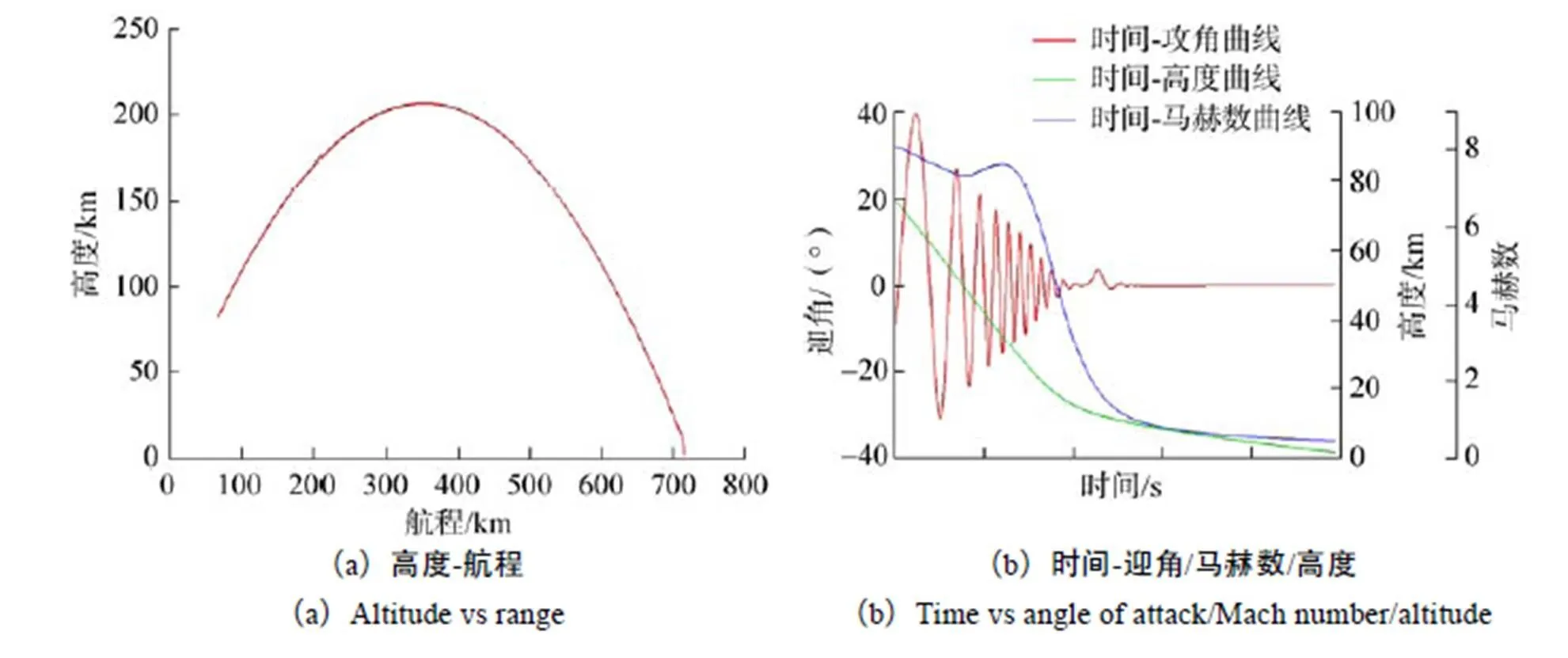
图9 有栅格翼火箭芯一级残骸基准弹道曲线
表1给出了火箭芯一级残骸有无栅格翼6自由度蒙特卡罗拉偏仿真结果的落点参数对比,可以看出,有栅格翼外形的所有落点参数散布范围都要小于无栅格翼外形,落点纵向和侧向航程的均方差约为无栅格翼外形的1/2.5,落地时刻的均方差约为无栅格翼外形的1/2,有栅格翼外形由于进入大气层后飞行迎角振荡收敛,导致了气动阻力比无栅格翼外形明显减小,从而飞行时间减小,有栅格翼外形落地总迎角在0°附近。
表1 拉偏仿真落点参数统计结果对比

Tab.1 Comparison of statistical results of different simulation parameters
图10给出了有无栅格翼外形火箭芯一级残骸落点散布拉偏仿真结果,可以看出,增加栅格翼后,由于火箭芯一级残骸自身具有气动稳定性,火箭芯一级残骸落点的散布范围明显缩小,对于无栅格翼外形,仿真得到的落点散布范围约为21.48km × 22.37km,该数值与文献[2]给出的40km × 30km落区范围上存在一定差异,主要原因是本文考虑的拉偏量与实际火箭拉偏量存在一定差异造成的。但总体来说,残骸落点分布的整体趋势与文献相一致。在有无栅格翼落点散布范围对比分析中,采用相同的拉偏方式,仿真获得了加装栅格翼后火箭芯一级残骸落点散布范围,约为10.03km × 11.28km,与无栅格翼外形相比,落点散布面积减小了约76%。
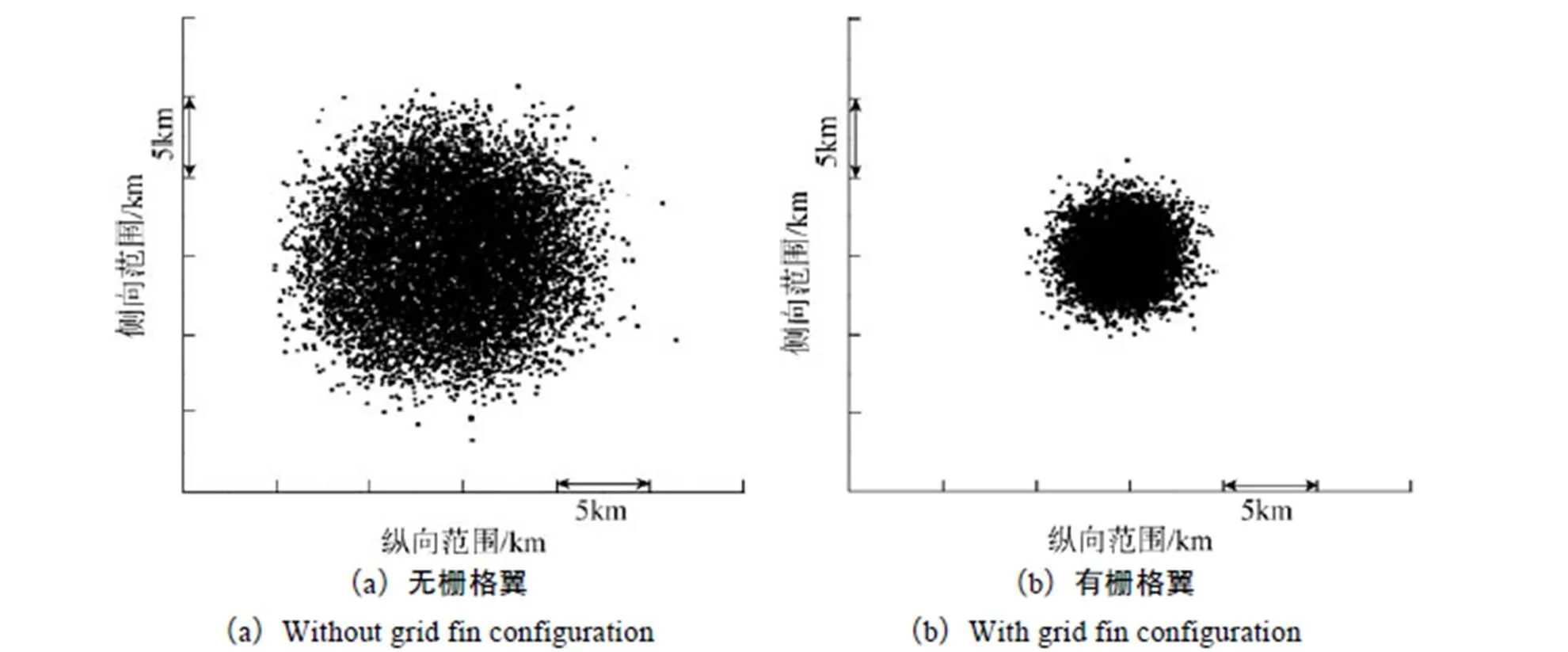
图10 火箭芯一级残骸有无栅格翼落点散布范围对比
图11给出了弹道拉偏仿真得到的火箭芯一级残骸有无栅格翼外形迎角—时间历程散布曲线,可以看出,对于无栅格翼火箭芯一级残骸,在中等迎角范围内俯仰静稳定,在小迎角范围内存在多个静稳定配平点,分别的±20°和0°附近;而火箭芯一级残骸加装栅格翼后,俯仰方向具有气动稳定性,再入过程中配平迎角在0°附近,进入大气层后飞行迎角振荡收敛,从而使得带栅格翼火箭芯一级残骸落点散布的范围明显减小。
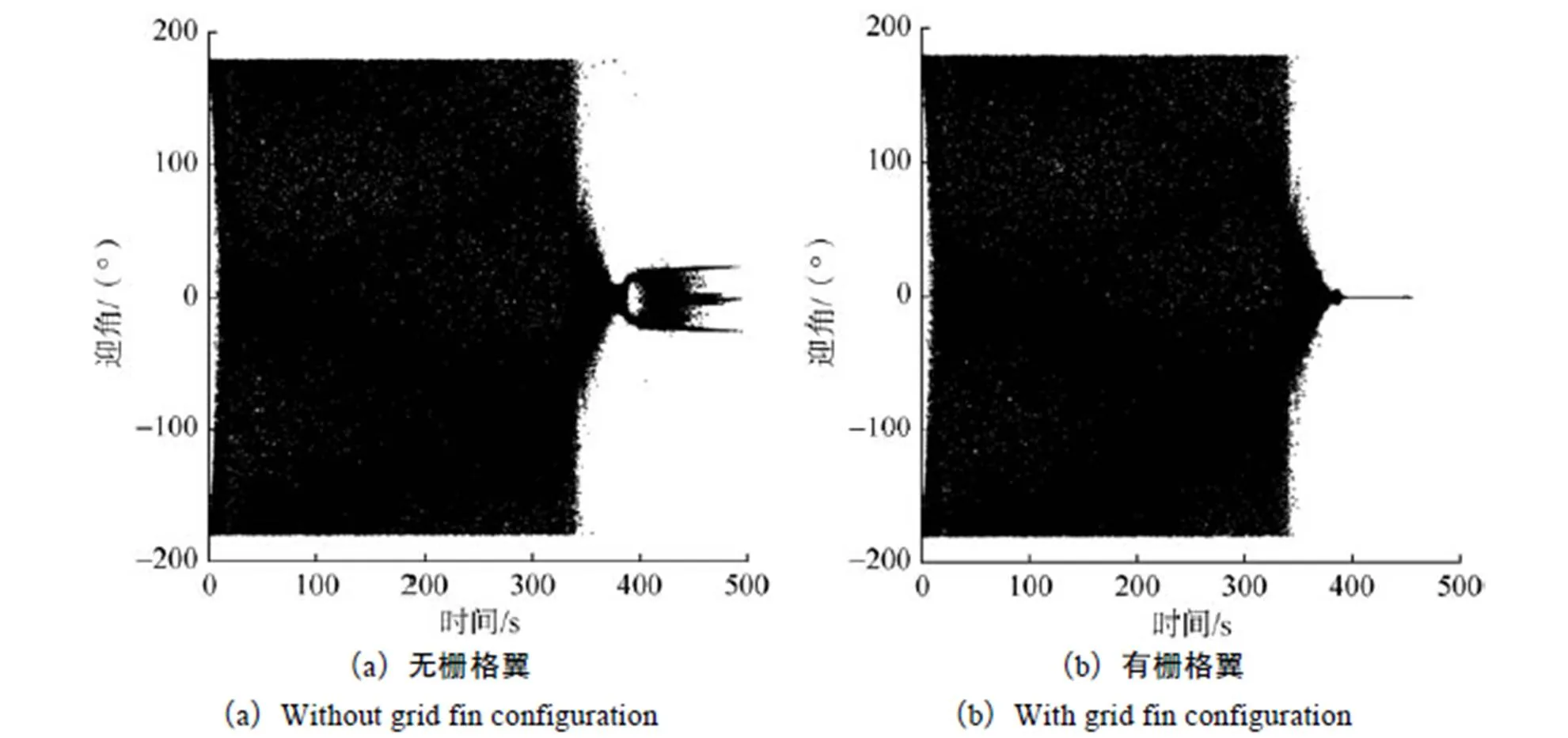
图11 火箭芯一级残骸有无栅格翼迎角—时间历程散布对比
4 结束语
利用栅格翼气动效率高、能够改变静稳定性的特点,本文探索了其在减小火箭芯一级残骸落点散布范围上的应用。本文设计的栅格翼单片质量约为150kg,上升段折叠安装,阻力增量较小;再入段栅格翼展开后,小迎角范围内火箭芯一级残骸压心后移明显,气动稳定性明显增强,配平迎角在0°附近,使得飞行迎角在进入大气层后迅速振荡收敛;蒙特卡罗弹道仿真结果显示,残骸落点散布面积减小约76%。本文研究的火箭芯一级加装栅格翼方案,可以大幅减小残骸落点散布范围,不需要增加额外复杂的控制机构,具有广阔的应用前景。
目前本文研究的火箭芯一级加装栅格翼方案仍属于无控飞行,下一步将设计栅格舵构型,降低上升段附加质量,开展栅格舵控制效率分析,规划火箭芯一级助推器下落弹道,设计制导率,结合姿控发动机复合控制技术,实现火箭芯一级的落点精确控制与回收。
[1] 杨勇, 王小军, 唐一华. 重复使用运载器发展趋势及特点[J]. 导弹与航天运载技术, 2002(5): 15-19. YANG Yong, WANG Xiaojun, TANG Yihua. Development Trends and Characteristics of Reusable Launch Vehicles[J]. Missiles and Space Vehicles, 2002(5): 15-19. (in Chinese)
[2] 肖松春, 宋建英, 安学刚. 基于蒙特卡洛方法的运载火箭残骸落区划定[J]. 装备指挥技术学院学报, 2010, 21(4): 66-70. XIAO Songchun, SONG Jianying, AN Xuegang. Describing Area of Level Point of Rocket′s Debris Based on Monte-carlo Method[J]. Journal of the Academy of Equipment Command & Technology, 2010, 21(4): 66-70. (in Chinese)
[3] 汪小卫, 张普卓, 吴胜宝, 等. 运载火箭子级回收技术研究[J]. 航天返回与遥感, 2016, 37(3): 19-28. WANG Xiaowei, ZHANG Puzhuo, WU Shengbao, et al. Recovery Technology of Launch Vehicle Stage[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(3): 19-28. (in Chinese)
[4] 黄伟. 运载火箭伞降回收着陆技术概述[J]. 航天返回与遥感, 2017, 38(3): 1-12. HUANG Wei. The Summary of Launch Vehicle Parachute Recovery and Landing Technologies[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(3): 1-12. (in Chinese)
[5] 赵祖虎. 航天飞机助推器轻型回收系统[J]. 航天返回与遥感, 1997, 18(4): 3-8. ZHAO Zuhu. Space Shuttle Solid Booster Lightweight Recovery System[J]. Spacecraft Recovery & Remote Sensing, 1997, 18(4): 3-8. (in Chinese)
[6] CARL M, ASHLEY T, JAMES B, et al. Ares I-x Separation and Reentry Trajectory Analyses[C]//AIAA Atmospheric Flight Mechanics Conference. AIAA 2011-6462. Portland, Oregon, 2011.
[7] ANTHONY T, PHILLIP D, ANTHONY T, et al. An Overview of the Landing System for the K-1 Launch Vehicle, Parachutes and Airbags[C]//AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. AIAA 1997-1515. SanFrancisco, CA, 1997.
[8] BARRY H, DANIEL T. Final Approach and Landing for a Winged Reusable Booster[C]//15th AIAA International Space Planes and Hypersonic System and Technologies Conference, AIAA 2008-2566, Dayton, Ohio, 2008.
[9] 郑雄, 杨勇, 姚世东, 等. 法尔肯9可重复使用火箭发展综述[J]. 导弹与航天运载技术, 2016(2): 39-46. ZHENG Xiong, YANG Yong, YAO Shidong, et al. Survey and Review on Development of Falcon 9 Reusable Rocket[J]. Missiles and Space Vehicles, 2016(2): 39-46. (in Chinese)
[10] 冯韶伟, 马忠辉, 吴义田, 等. 国外运载火箭可重复使用关键技术综述[J]. 导弹与航天运载技术, 2014(5): 82-86. FENG Shaowei, MA Zhonghui, WU Yitian, et al. Survey and Review on Key Technologies of Reusable Launch Vehicle Abroad[J]. Missiles and Space Vehicles, 2014(5): 82-86. (in Chinese)
[11] RAVINDRA K, NIKHIL V S, BALAKRISHNAN N. CFD Simulation of the Grid Fin Flows[C]//The 31stAIAA Applied Aerodynamics Conference. San Diego, CA, June 24-27, 2013.
[12] THEERTHAMALAI P. Effect of Geometric Parameters on the Aerodynamic Characteristics of Grid-fin Cells at Supersonic Speeds[R]. AIAA 2007-690.
[13] LIN H, HUANG J C, CHENG C. Navier-stokes Computations for Body/Cruciform Grid Fin Configuration[J]. Journal of Spacecraft and Rockest, 2003, 40(1): 30-38.
[14] 任怀宇, 蔡昱, 孙洪森. 高超声速栅格翼气动特性研究[J]. 宇航学报, 2010, 31(1): 44-49. REN Huaiyu, CAI Yu, SUN Hongsen. Study on Aerothermodynamics of Hypersonic Grid Fin[J]. Journal of Astronautics, 2010, 31(1): 44-49. (in Chinese)
[15] 吴晓军, 陈红全, 邓有奇, 等. 栅格翼绕流数值模拟研究[J]. 空气动力学报, 2009, 27(1): 78-82. WU Xiaojun, CHEN Hongquan, DENG Youqi, et al. CFD Analysis of Grid Fins[J]. Acta Aerodynamica Sinica, 2009, 27(1): 78-82. (in Chinese)
[16] 张耀冰, 邓有奇, 吴晓军, 等. DLR-F6翼身组合体数值计算[J]. 空气动力学报, 2011, 29(2): 163-169. ZHANG Yaobing, DENG Youqi, WU Xiaojun, et al. Drag Prediction of DLR-F6 using MFlow Unstructured Mesh Solver[J]. Acta Aerodynamica Sinica, 2011, 29(2): 163-169. (in Chinese)
[17] CHEN J T, ZHANG Y B, ZHOU N C, et al. Numerical Investigations of the High-lift Configuration with MFlow Solver[J]. Journal of Aircraft, 2015, 52(4): 1051-1062.
[18] MA M S, DENG Y Q, ZHENG M, et al. Navier-stokes Computations for a Grid Fin Missile[C]//The 23rdAIAA Applied Aerodynamics Conference. Toronto,Canada, 2005.
[19] MONTGOMERY C, HUGHSON, ERIC L B. Transonic Aerodynamic Analysis of Lattice Grid Tail Fin Missiles[C]//The 24thApplied Aerodynamics Conferernce. San Francisco, California, 2006.
[20] ABATE G, WINCHENBACH G, HATHAWAY W. Transonic Aerodynamic and Scaling Issues for Lattice Fin Projectiles Tested in a Ballistic Range[C]//Proceedings of the 19thInternational Symposium of Ballistic. Interlaken, Switzerland, 2001.
[21] ZENG Y, CAI J S, DEBIASI M, et al. Numerical Study on Drag Reduction for Grid Fin Configurations[R]. AIAA 2009-1105.
Application Research of Grid Fin on Reducing the Falling Point Distribution for the Debris of Rocket
JIA Hongyin XU Mingxing ZHANG Peihong WU Xiaojun HE Zhengchun
(China Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang, 621000, China)
The characteristics of grid fin with high efficiency and high aerodynamic drag are applied to reduce the falling point distribution for the first stage debris of rocket. First of all, the numerical methods for the aerodynamic characteristics of gird fin are introduced. The reliability of the numerical method is verified by comparison of the results with the experimental data. And then the research on the design of the gird fin for the rocket booster is carried out. The aerodynamic performance of the first stage debris of rocket with grid fin at subsonic and supersonic is analyzed. The falling point distribution range of the first stage debris before and after installing grid fin are compared by six degrees of freedom Monte Carlo trajectory simulation. The results indicate that the drag increment is very small when the rocket with folded grid fin rises up. The drag increases less than 2% at supersonic condition. When making a reentry with the grid fin unfolded, the first stage debris has aerodynamic stability and trim angle of attack near 0 degree. The attitude of the debris convergence rapidly during reentry. After installation of the grid fin, the range of falling point distribution of the first stage debris is reduced by 76%. The grid fin has wide application prospects in reducing the falling point distribution for the first stage debris of rocket.
grid fin; aerodynamic stability; falling point distribution; trajectory simulation; rocket; aerospace recovery
V525
A
1009-8518(2018)06-0021-09
10.3969/j.issn.1009-8518.2018.06.003
2018-05-05
国家重点研发计划战略高技术重点专项(17H86303ZT001018)
贾洪印,男,1985年生,2011年获中国空气动力研究与发展中心硕士学位,助理研究员。主要研究方向为计算空气动力学。E-mail:hongyinjia@foxmail.com。
(编辑:庞冰)
