一种引用全相参技术的连续波相位测距方法
2019-01-05汪瀚文张丕状
汪瀚文, 张丕状
(中北大学 信息探测与处理重点实验室, 山西 太原 030051)
0 引 言
随着现代化科学技术的日益发展, 在各个应用领域中, 测距仪器的应用范畴越来越广泛, 对于测距仪测量的要求也越来越高. 为了追求更高的测量范围和测量精度, 人们不断地研究新的测距方法和技术[1].
连续波相位测距[2]因测量精度高、 近距离不存在盲区、 测距精度与距离无关等优点, 被广泛应用于测距技术领域, 是公认的最有发展潜力的绝对距离测量技术. 连续波相位测距中连续波的相位信息能够反映出所测距离长度, 因此相位信息的准确度将直接影响测距系统的精确度. 因而提高测距精度[3]的关键之一在于鉴相技术的改进[4].
发射波的调制信号频率和数据采集的采样频率会影响相位信息, 而信号频率和采样频率都是由晶振提供的, 每一个晶振的频率都不是完全精确的, 而是存在一定的误差值, 且不同晶振的误差值也不尽相同. 晶振频率的误差会使得信号频率和采样频率产生相应的误差, 从而使得测量的相位值产生误差, 最终影响测距系统的精度.
相参技术早在声学和光学中就有应用, 之后应用于雷达系统[5], 其中雷达发射信号频率、 本振信号频率和相参基准信号频率全部由自主震源频率提供, 从而保持稳定的相位同步关系.
本文旨在提出一种引用雷达“全相参”[6]技术的方法, 通过同一晶振给发射信号和数据采集提供震源, 使信号频率和采样频率的误差值同步, 从而降低因晶振频率的误差产生的测量误差, 进而提高测量的精确度.
1 向量内积鉴相法原理
内积鉴相法[7]的算法原理是基于一个信号与初始相位为零的信号的相位差, 它是通过傅里叶变化推导出来的, 推导过程为:
按照傅里叶级数的定义[8], 若三角函数y(t)的周期为T, 角频率为ω, 其傅里叶级数展开式为
(1)
式中:n为正整数, 各次谐波成分的幅度值为:
直流分量的幅度
(2)
余弦分量的幅度
(3)
正弦分量的幅度
(4)
式中:n=1,2,3,….
若将式(1)中的同频率项加以合并, 可以写成另一种形式
(5)
比较式(1)和(5)可以看出傅里叶级数中各个量之间的关系:
a0=c0,
an=cncosφn,
bn=-c0sinφn.
(6)
因此, 由式(6)中的各关系可推出
(7)
则
(8)
由以上推论可得: 对于余弦信号
y(t)=Acos(2πft+φ),
(9)
则其相位差
(10)
式中:
(11)
式中:n为采样点数;fs为采样频率, 则其对应的数字信号的相位差
(12)
2 引用全相参技术的测相方法
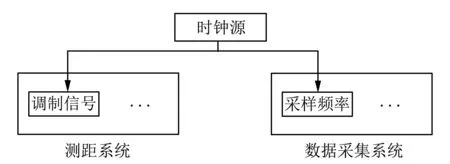
图 1 引用全相参的测距系统结构图Fig.1 Reference to the structure of the ranging system of the full coherence
在向量内积鉴相法中[9], 调制信号的频率和数据采集的采样频率会直接影响鉴相结果. 在实际应用中, 由于提供调制信号频率的晶振和数据采集中采样频率的晶振都不是完全精准的, 导致调制信号的频率和数据采集的采样频率都会存在不同的偏差, 这些偏差都会使得鉴相结果产生不同程度的误差, 最终影响测距系统的精确性.
在此情况下, 我们在向量内积鉴相法中引用全相参技术[10], 对于调制信号频率和数据采集的采样频率, 我们全部由同一自主震源频率提供, 保证了调制信号频率和采样频率误差的同步性, 如图 1 所示.
3 理论分析
假设测距系统对距离L的目标物体进行测量.
测距系统的发射信号为
y(t)=A0cos(ωt).
(13)
测距系统的接收回波信号为
y(t)=Acos(ωt+φ).
(14)
数据采集系统以fs的采样频率对接收的回波信号进行采样.
当不引用全相参技术时, 即信号频率和采样频率不来自同一震源频率, 因此调制信号频率和采样频率的误差值不同步. 假设调制信号频率的误差度为k, 采样频率的误差度为d, 则调制信号频率为f0+k*f0, 采样频率为fs+d*fs.
由式(12)可得相应的相位差
(15)
对式(15)的分子求导可得
(16)
则分子误差
(17)
同理可得分母误差
(18)
当引用全相参技术时, 信号频率和采样频率全来自同一震源频率, 因此调制信号频率和采样频率的误差值同步. 假设调制信号频率和采样频率的误差度均为k, 则调制信号频率为f0+k*f0, 采样频率为fs+k*fs.
由式(12)可得相应的相位
(19)
对式(19)的分子求导可得
(20)
则分子误差
(21)
同理可得分母误差
(22)
由式(17), (21) 对比和式(18), (22)对比可知, 在全相参条件下的相位差误差度比在非相参条件下的误差度更小.
4 仿真分析
试验中, 测量距离从2~25 m, 每隔0.1 m取一个测量点. 在理想测量条件下, 信号频率为5 kHz, 采样频率为1 MHz. 在实际情况中, 信号频率和采样频率均存在一定误差值. 假设在全相参条件下, 信号频率和采样频率由同一误差值为1%的晶振提供; 在非相参条件下, 信号频率由误差值为1%的晶振提供, 采样频率由误差值为2%的晶振提供. 通过Matlab仿真后, 分别得到在理想条件、 全相参条件、 非相参条下测量距离和信号相位的关系曲线(见图 2)和全相参条件、 非相参条件下测量距离和相位误差度的关系曲线(见图 3).
由图2测量距离和信号相位差的曲线图可知: 在全相参条件下测得的回波信号和发射信号的相位差与在非相参条件下测得的回波信号和发射信号的相位差进行对比, 全相参条件下回波信号和发射信号的相位差更接近理想情况下回波信号和发射信号的相位差.
由图3测量距离和相位误差度的曲线图可知: 在全相参条件下测得的回波信号和发射信号的相位差的误差度要比在非相参条件下测得的回波信号和发射信号的相位差的误差度要更小, 因此在全相参条件下测距系统的精确度更高.
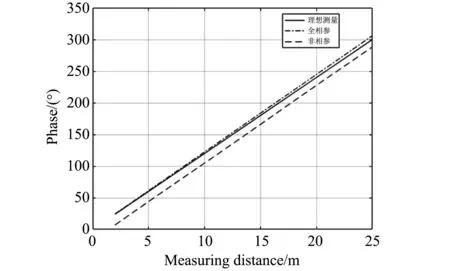
图 2 测量距离和信号相位的曲线图Fig.2 Measuring distance and signal phase

图 3 测量距离和相位误差的曲线图Fig.3 Measuring the distance and phase error
5 结 论
本文在提高测距精确度的背景下, 提出一种引用全相参技术的连续波相位测距方法, 通过理论分析和仿真验证, 证实了该方法能有效提高测距系统的精确度, 具有一定的应用价值.
