基于CFD-DEM的饲料调质器物料运动模拟与试验

彭 飞 方 芳 王红英 黄志刚 付宗强 高东明

(1.北京工商大学材料与机械工程学院， 北京 100048; 2.郑州大学化工与能源学院， 郑州 450001;3.中国农业大学工学院， 北京 100083)

0 引言

饲料作为动物主要的食物来源，是畜禽和水产养殖业的物质基础，2017年全国饲料总产量达到2.24亿t[1]。调质是饲料加工过程中非常关键的环节，是影响颗粒饲料质量的重要因素[2]。但由于调质器作业过程的封闭性、湿黏饲料原料物性的复杂性，目前国内外对调质过程的机理和调质器作业的性能研究较少，难以进行精确的定量分析[3]。

离散元法(Discrete element method，DEM)是分析颗粒离散体物料的一种方法，1971年由美国Cundall教授基于分子动力学原理提出，被大量应用在复杂物理场作用下粉体动力学现象、具备较为复杂结构的材料力学特性和多相混合材料介质等研究中，涉及粉体生产加工、研磨和混合搅拌等生产实践领域[4-6]。计算流体动力学(Computational fluid dynamics，CFD)能够很好地模拟流体在腔体内的气压分布和特定层面的速度分布，目前针对调质器工作过程的仿真模拟还比较少，前人做过类似调质器结构的建模研究[7-10]。DEM能够构建黏性颗粒模型，还可以与CFD耦合计算。李洪昌等[11]通过CFD-DEM耦合方法模拟了风筛式清选装置中物料在筛面上的运动，其中物料使用EDEM建模，连续流体使用CFD建模，研究并分析入口气流速度对该装置筛分性能的影响。刘佳等[12]基于CFD-DEM耦合方法，模拟了机械气力组合式精密排种器的工作过程，模型采用EDEM软件中的bonding和API替换的方法，建立了非球形虚拟玉米颗粒。彭飞[13]初步构建了调质器CFD-DEM耦合模型，但是该模型仅局限于定性描述，缺乏试验数据和定量分析等，模型的可靠性与合理性尚未验证，存在一定的局限和不足。以上文献为深入分析与研究调质器CFD-DEM耦合模型提供了理论基础和方法参考。

本文应用CFD-DEM耦合计算方法，分析饲料原料在调质器内的运动和黏结情况。基于构建的调质器耦合模型，通过三因素五水平正交回归模拟试验，分析桨叶安装角、调质轴转速、填充率3个因素对其出料量的影响，并利用试验装置进行试验验证，为调质器结构设计和作业参数优化提供参考。

1 调质器结构和工作原理

如图1所示，调质器部件主要由进料单元和调质单元组成，具体包括：进料口、进料螺旋、蒸汽腔、蒸汽进口、调质器外壁、主轴、桨叶、调质腔、出料口及联轴器等[14-15]。

图1 饲料调质器结构简图Fig.1 Structure diagram of feed conditioner1.进料口 2.进料螺旋 3.蒸汽腔 4.蒸汽进口 5.调质器外壁 6.调质器主轴 7.桨叶 8.调质腔 9.出料口

蒸汽进口位于调质单元物料进入处，并与调质腔体连通。在调质器驱动电动机和变频器的带动下，进口螺旋叶片推动原料至调质腔内；蒸汽发生器产生蒸汽，经蒸汽腔、环形分布的蒸汽加工孔，进入到调质腔内；在调质腔内旋转扇形桨叶的搅拌作用下，饲料原料和蒸汽受到挤压、剪切、翻滚和抛出等强制混合作用，在剧烈的相对运动中均匀混合并产生水热反应，由出料口流出，完成调质过程。

2 调质器CFD-DEM数值模拟

2.1 数学模型

利用CFD-DEM耦合模拟时，耦合模型主要分为Lagrangian模型和Eulerian模型[16]。其中，Eulerian模型考虑了颗粒对流场的影响(适用于颗粒相占总体积大于10%的情况)[17]，根据饲料调质器作业实际工况，原料试验颗粒对流体相的作用明显，因此本文采用Eulerian模型对饲料原料调质过程进行模拟。考虑到原料对流场的影响，在守恒方程中加入一个额外的体积分数，即

(1)

式中ε——气体体积分数

ρ——气体密度，kg/m3

t——时间，s

u——气体速度，m/s

动量守恒方程为

(2)

其中

式中g——重力加速度，m/s2

μ——气体动力黏度，Pa·s

S——动量汇，即作用在网格单元内流体阻力的总和，N/m3

Fi——第i颗粒对气流的阻力，N

V——网格单元的体积，m3

由于饱和蒸汽对饲料原料的影响主要为曳力，故选择Free-stream阻力模型，该自由流阻力的计算公式为

Fd=0.5CDρA|v|v

(3)

式中CD——单个颗粒单元的曳力系数

A——颗粒投影面积，m2

v——气体相对颗粒单元的流动速度，m/s

饲料颗粒的曳力系数CD取决于雷诺数Re，其计算公式为

(4)

其中

式中L——原料颗粒直径，m

α——CFD网格单元的自由体积，m3

针对仿真对象的不同，选择相应的接触模型[17]。由于饲料原料进入调质器后处于湿黏状态，为典型的黏性散粒体，需要引入黏结键来表征颗粒彼此接触时的运动状态。Hertz-Mindlin计算颗粒间法向和切向黏结力分别定义为Fn、Ft，法向和切向黏结力矩分别为Tn、Tt，单个颗粒法向和切向的速度分别为vn、vt，单个颗粒法向和切向的角速度分别为ωn、ωt。黏结力Fn、Ft和力矩Tn、Tt随着时间步长的增加，按公式从零开始增加。

(5)

式中RB——黏结半径，m

δt——时间步长，s

Sn——颗粒法向刚度，N/m

St——颗粒切向刚度，N/m

A1——颗粒间的接触面积，m2

当法向和切向应力超过某个定义值时，黏结就会被破坏。因此，定义法向应力最大值σmax和切向应力最大值τmax为

(6)

2.2 调质器建模与仿真

构建调质器内腔几何模型，采用Fluent 12.0对调质器内腔模型进行参数设置，采用Fluent 12.0中的DEM模块对散粒体参数进行设定，DEM由软件EDEM 2.2求解，两者耦合安装并计算，耦合方法的基本思路：利用CFD方法计算压力场及流场分布，利用DEM方法计算颗粒系统的受力和运动情况；两者基于一定的模型进行质量、动量和能量等物理量的作用与交换，实现耦合计算。

2.2.1结构模型构建和参数设置

基于调质器尺寸，构建调质器Pro/E模型，步骤如下：

(1)调质腔模型主要几何参数：圆柱腔体直径为100 mm，长度为600 mm；空心主轴位于腔体中心，直径30 mm，长度与调质腔相同；扇形桨叶共18组，距离调质腔内壁2 mm，按轴向间隔30 mm、径向间隔90°分布，安装角度可调；蒸汽进口为10组，直径为6 mm，呈环形均匀分布于调质腔进料口处的端盖上；出料口位于调质腔右端40 mm，其结构为Φ24 mm的圆柱体。由于装配体零件较多，模型导入到Gambit软件时，导致Gambit模型中线、面、体较多，达到上千个，不便于下一步在Fluent软件中设置边界类型和边界条件以及后续的模拟计算，因此需要对模型进行简化。使用Pro/E 4.0建立零件1(调质器内腔)、零件2(调质轴与桨叶)这两个零件(图2、3)，然后进行装配。

图2 调质器内腔几何模型Fig.2 Geometric model of conditioner inner cavity

图3 调质轴与桨叶几何模型Fig.3 Geometric model of conditioner shaft and blade

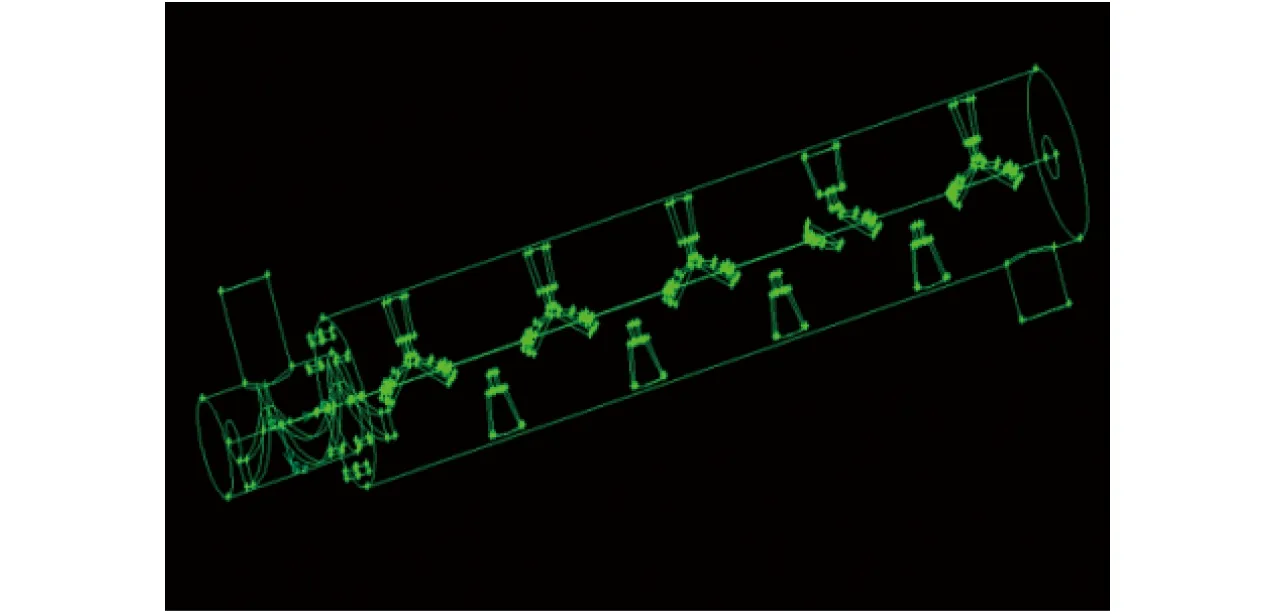
图4 Gambit中调质器模型Fig.4 Model of conditioner in software Gambit

图5 利用Gambit对模型进行边界条件设置和网格划分的结果Fig.5 Boundary condition setting and meshing of model by using Gambit

(2)将装配体保存为igs格式并导入到Gambit 2.4.6中(图4)，得到由2个独立构件组成的几何体，共计226个面；结合实际作业情况和边界类型设定方法，将这些面定义为4种类型：进气口(inlet)、出气口(outlet)、壁面(wall)、旋转部分(wall)。对图4所示模型进行体网格划分，网格尺寸为8 mm，零件1得到219 205个网格，零件2得到21 938个网格，结果如图5所示；最后将划分完成后的装配体以mesh格式保存，作为Fluent的mesh文件。

(3)将mesh文件导入到Fluent，流体模型采用RNGk-ε黏性模型；设置进气口为压力入口，出气口为压力出口；基于物料所占腔体体积比例，选择Eulerian法进行耦合，耦合参数匹配设置方法参考文献[18-19]。调质过程中，原料与饱和水蒸气发生传热传质反应，原料含水率由10%～12%增加到17%～19%，物料黏度增加；基于容重法国标[20]，测得该含水率范围条件下，饲料物料密度平均值为443 kg/m3；在EDEM中将物料间离散元参数设置为黏结模型(Hertz-Mindlin with bonding)。EDEM模型中材料参数设置如表1所示。

表1 EDEM模型中材料参数设置Tab.1 Material parameter setting of EDEM model

(4)其它参数设置：设置离散元模型中时间步长为2×105s，为瑞利时间步长的14%，该值在瑞利时间步长比例的建议范围之内，保存时间间隔为0.01 s。设置颗粒生成量为unlimited number。由于该调质器调质时间为15～25 s，为便于模拟调质器稳定工作前及稳定工作一段时间后的作业状况，仿真时间应适当大于实际生产达到稳定的调质时间，因此在EDEM中将仿真时间设置为30 s。

2.2.2调质过程仿真分析

仿真预试验时，试验因素均设定为零水平，分别是：桨叶安装角为45°、调质轴转速为250 r/min、填充率为35%。图6为调质器仿真模拟30 s过程中迭代收敛曲线，由图分析可知，仿真收敛性较好，在0～30 s内调质器内部的流场速度趋于平稳。在EDEM中统计并分析调质器内颗粒数量随时间变化情况，结果如图7所示，可以看出，大概在25 s以后，整个腔体内的颗粒数目趋向稳定、基本不再增加或减少，即进料口和出料口颗粒数量基本维持平衡，此时调质器模型趋于稳定状态，可以用于模拟调质器实际生产中达到稳定的过程。

图6 调质器模拟工作30 s过程中迭代收敛曲线Fig.6 Iterative convergence curves of simulation during 30 s

图7 0～30 s过程中调质器内颗粒数量变化曲线Fig.7 Changing curve of particle number in conditioner during 0～30 s

2.3 仿真结果与分析

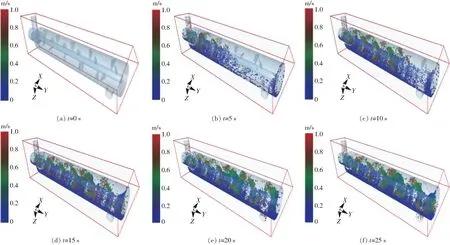
图9 0～25 s调质器稳定工作前颗粒分布和运动状态Fig.9 Particle distribution and movement during 0～25 s

图8a、8b分别为30 s时调质器速度场与压力场分布图，由垂直的两个截面显示。由图可以看出，10个蒸汽进口处气体流速较大；随着不断远离蒸汽进口，气体流速逐渐减慢；沿着物料运动方向，速度场与压力场整体变化均匀。在调质器作业过程中，蒸汽与原料颗粒充分接触并发生水热反应，这与该调质器结构和调质工作原理基本一致。

图8 30 s时调质器速度场与压力场分布图Fig.8 Velocity and pressure field in conditioner at 30 s

在DEM模型中分别统计0、5、10、15、20、25 s情况下调质器内颗粒的运动和分布情况，结果如图9所示。由图可知，在该时间段内，颗粒一直不断生成，调质器进料速率大于出料速率，因此调质腔内颗粒物料不断增多，腔体物料填充率不断提高；同时调质轴旋转并带动桨叶搅拌颗粒物料，桨叶有一定的安装角度，旋转的桨叶起到搅拌、抛起并推动物料前进的作用，在25 s左右进出调质器腔的颗粒数量基本持平，此时填充率基本不再变化，这与调质器开始作业阶段的真实状态基本一致。图10为调质器稳定工作过程阶段，此阶段腔体内颗粒数目和填充度变化不大，基本处于稳定的状态。由图10f可知，颗粒黏结在一起呈团簇状，调质反应后的物料也呈团簇状被翻起搅拌，与实际生产情况相符合，可知选用的颗粒黏结模型基本合理；由颗粒速度分布规律可知，颗粒受到桨叶的搅拌作用，不断被抛起并向前推进，在调质腔中部及上部、靠近桨叶末端处速度较快；靠近调质器底部颗粒的运动速度较慢，有可能导致物料黏附在该处内壁上、产生积料现象，该模拟过程基本与调质器作业过程一致。物料速度场与压力场分布均匀，颗粒前进方向与蒸汽进气方向一致、两者接触较充分，该模型整体作业过程较为合理，可以用于模拟调质器作业时饲料原料的分布和运动情况。

图10 26～30 s调质器稳定工作后颗粒分布和运动状态Fig.10 Particle distribution and movement during 26～30 s

3 试验设计与指标测定

3.1 试验设计

由预试验及文献[21-22]可知，调质器工作性能的主要影响指标为桨叶安装角、调质轴转速、填充率，故本文选择上述3个因素进行仿真试验研究。根据理论分析、单因素预试验结果、调质器结构参数与生产实际，确定各试验因素的取值范围为: 桨叶安装角10°～80°、调质轴转速150～350 r/min、填充率10%～60%。以桨叶安装角X1、调质轴转速X2、填充率X3为试验变量，基于二次正交旋转组合试验原理，建立因素编码表如表2(x1、x2、x3为各变量真实值)所示。

表2 二次回归正交试验设计因素编码Tab.2 Factors and levels of quadratic regression orthogonal rotating experiment design

3.2 指标测定

调质器在调质作业过程中的工作效率可以通过出料口处的出料量来检测。通过EDEM软件的数据导出工具Export Results Data，导出数据并计算出仿真过程中调质器的出料量。

4 试验结果与分析

4.1 回归模型建立

以各影响因素编码值为自变量，以仿真结果测得的出料量Y为评价指标，依据二次回归正交旋转组合设置不同试验组的模型参数，基于CFD-DEM耦合仿真试验，结果如表3所示(X1、X2、X3为各变量编码值)。

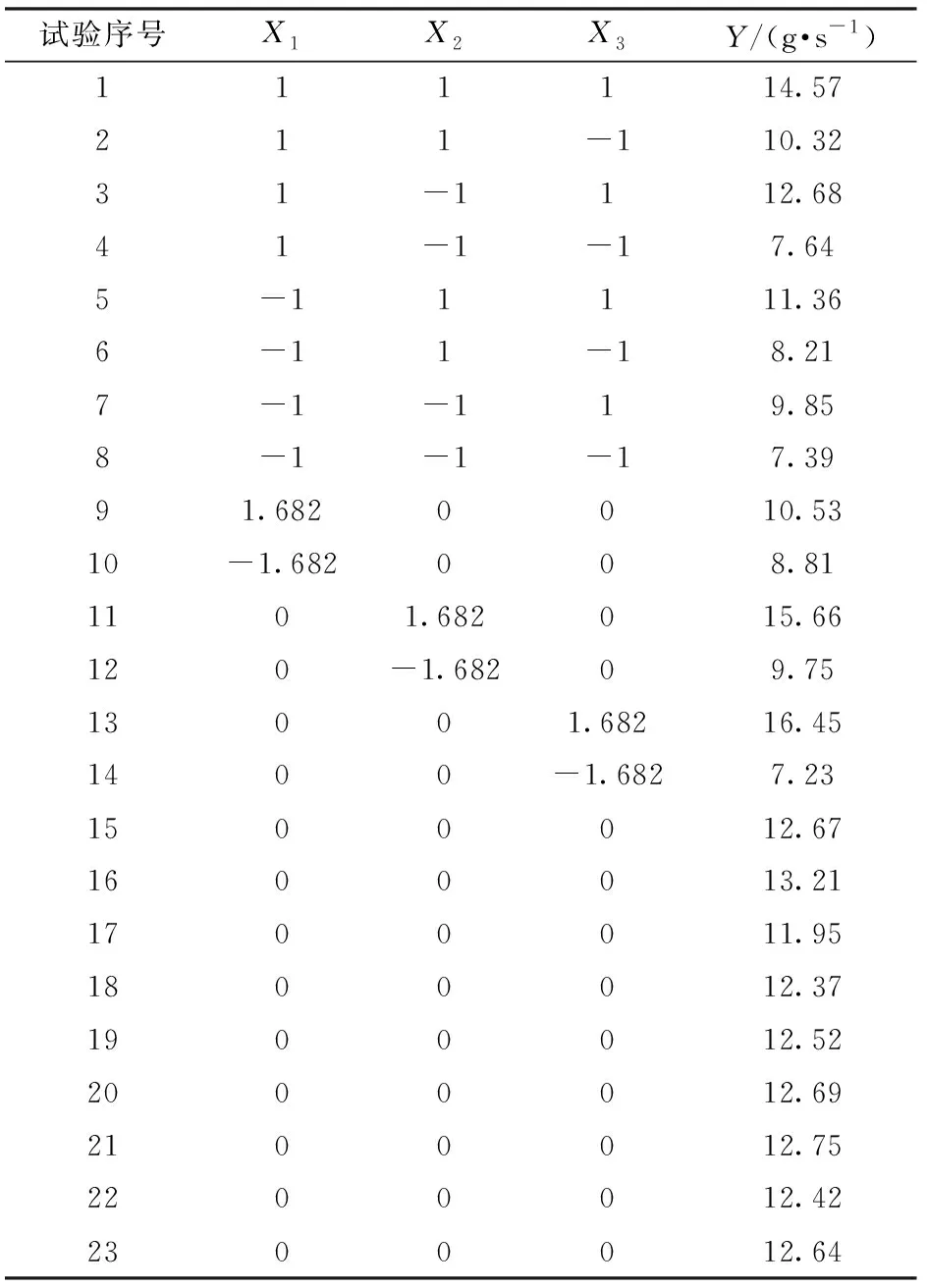
表3 二次回归正交旋转组合试验设计与结果Tab.3 Experimental design and results of quadratic regression orthogonal rotating test

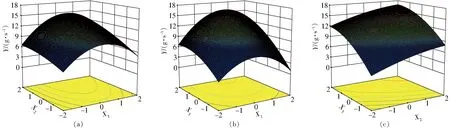
图11 基于响应面法的参数组寻优结果Fig.11 Optimization of parameter group by using response surface method

变异来源平方和自由度均方FP模型129.13914.3516.80<0.0001X19.3419.3410.930.0057X220.76120.7624.310.0003X367.70167.7079.27<0.0001X1X20.6310.630.730.4070X1X31.6911.691.980.1826X2X301000.9701X2124.95124.9529.210.0001X220.5210.520.600.4513X233.7513.754.390.0563

采用Design-Expert软件对试验进行回归分析，得到桨叶安装角X1、调质轴转速X2、填充率X3与调质器出料量Y的回归方程

(7)

4.2 回归模型寻优

为直观地分析试验因素与评价指标之间的关系，根据各回归项对评价指标的影响，结合简化回归模型，用“降维法”将任意1个因素固定中心水平[23-24]，得到另外2个试验因素与评价指标之间的降维回归模型，由Design-Expert软件绘制响应面图，分析各因素对出料量的影响，结果如图11所示。

在试验范围内，将填充率X3固定在中心水平上，得到桨叶安装角X1和调质轴转速X2的交互作用对调质器出料量的影响。由图11a可知，桨叶安装角和调质轴转速对出料量的影响为上凸型曲面；当调质轴转速一定时，出料量随桨叶安装角的增加呈现先增大后减小的趋势，这是因为物料在调质器中主要有轴向和径向两种运动形式，当桨叶安装角较小时，桨叶主要带动物料围绕调质轴转动，轴向推动力较小，因此物料轴向向前运动较弱，出料量较小；随着桨叶安装角的增大，物料轴向推进作用增强，出料量随之增加；随着桨叶安装角的进一步增大，桨叶对物料轴向推进作用减弱，主要起到切割物料作用，既不能推进也不能抛起物料。X1和X2的交互作用不显著。

在试验范围内，将调质轴转速X2固定在中心水平上，得到桨叶安装角X1和填充率X3的交互作用对调质器出料量的影响。由图11b可知，桨叶安装角和填充率对出料量的影响为上凸型曲面；当桨叶安装角一定时，出料量随填充率的增加呈现增大的趋势，且变化幅度随安装角的增大呈现先逐渐加剧、后逐渐减缓的规律。根据仿真情况及调质器输送机理分析，这可能是因为原料靠近桨叶部分出现的翻滚现象造成的。当填充率较低时，大量物料集中于远离调质轴的区域，径向速度低而轴向速度高；随着填充率的增大，更多的原料堆积使得靠近调质轴的原料增多，物料轴向速度变慢，因此出料量增加，但是增长速度变小。杨洋[25]基于离散元法和正交试验研究了粮食输送器的输送效率，罗胜等[26]研究了螺旋不连续加料装置的出料量变化，有相似的规律和结论。X1和X3的交互作用不显著。

在试验范围内，将桨叶安装角X1固定在中心水平上，得到调质轴转速X2和填充率X3的交互作用对调质器出料量的影响。由图11c可知，调质轴转速和填充率对出料量的影响为上凸型曲面；调质轴转速一定时，出料量随填充率的增加呈现增大的趋势；填充率一定时，出料量随桨叶安装角的增加呈现先增大后减小的趋势。X2和X3的交互作用不显著。

4.3 最优参数组合的确定及验证

由于该调质器最大生产率为50 kg/h，取最大生产率的90%～95%为宜，故Y在该范围内为宜。基于响应面法，运用Design-Expert软件中Optimization模块进行参数优化，在-1.682≤Xi≤1.682 (i=1，2，3)范围内对各参数进行进一步寻优，获得调质器最优作业参数组合为：X1=-0.31、X2=-1.13、X3=1.56，即x1=38.49°、x2=182.2 r/min、x3=58.4%，此时调质器出料量Y可获得最优目标值，仿真预测值为13.1 g/s。

5 样机试验

取最优参数组合，在北京市密云区昕三峰饲料厂进行调质器部件车间试验，如图12所示；加工对象为正常生产的乳猪料原料，物料理化指标良好。调整设备至最优参数组合，待调质器工作稳定后，测得调质器出料量实测值为12.8 g/s，其它指标性能良好，测得效果基本与优化试验结果一致，满足调质器实际生产需求。

图12 调质器生产试验Fig.12 Prototype working in workshop

6 结论

(1)基于离散单元法建立了饲料原料黏结颗粒模型，运用CFD-DEM耦合计算方法，对调质器原料颗粒进行运动和分布、颗粒黏结情况的耦合仿真。分别统计0～30 s阶段时调质器内颗粒的运动和分布情况，由仿真分析可知，原料受桨叶的搅拌作用，不断被抛起并向前推进，在调质腔中部及上部、靠近桨叶末端处速度较快；靠近调质器底部颗粒的运动速度较慢，有可能导致物料黏附在该处内壁上、产生积料现象。

(2)基于CFD-DEM耦合模型，通过三因素五水平正交组合试验，得出各因素对其出料量的影响显著性顺序依次为：填充率、调质轴转速、桨叶安装角。通过Design-Expert软件对试验结果进行回归分析和响应面分析，得到调质器最优作业参数组合为：桨叶安装角38.49°、调质轴转速182.2 r/min、填充率58.4%，此时出料量仿真值为13.1 g/s，试验值为12.8 g/s。通过对比仿真值和试验值，验证了仿真试验与回归模型的有效性。