基于节曲线凸性判别的行星轮系移栽机构解析
2019-01-05徐亚丹黄恒敏王振飞张国凤武传宇
孙 良 徐亚丹 黄恒敏 王振飞 张国凤 武传宇
(1.浙江理工大学机械与自动控制学院, 杭州 310018; 2.浙江省种植装备技术重点实验室, 杭州 310018;3.杭州职业技术学院, 杭州 310018)
0 引言
非圆齿轮行星轮系机构广泛应用于移栽机构、剑杆织机引纬机构、RCM机构等各种机械[1-5]。常用的设计方法有正向设计法与反向设计法。正向设计法通过调节轮系齿轮节曲线的形状获得满足设计要求的运动轨迹,反向设计法基于给定轨迹通过刚体导引等方法求解机构参数[6]。以上两种设计方法在实际应用过程中尚存在许多问题:正向设计法盲目性大,轨迹形状与轮系齿轮节曲线形状之间的关系不明确,难以获得满足设计要求的理想轨迹;反向设计法虽然给定了满足设计要求的理想运动轨迹,但是求解出的齿轮节曲线形状凹凸变形程度大,难以获得合理的非圆齿轮。另外通过给定的运动轨迹求解出的机构参数存在尺寸不合理和在回转过程中机构双臂干涉的情况。
针对上述问题,本文提出一种基于非圆齿轮节曲线形状和机构尺寸优化的轨迹反求方法。在反向设计法的基础上,将实现平面运动轨迹的行星轮系机构简化为平面开链二杆机构。在轨迹平面所在的全局坐标系内,通过对轮系中心解析区域内单行星架轮系机构非圆齿轮节曲线凸性值和杆长参数的求解,给出约束条件下的理想参数解域。通过设置解析区域给定轮系中心点在参考坐标系内的变化范围,求解在解析区域内实现给定轨迹的轮系机构参数和齿轮节曲线凸性值。根据解析区域的求解结果,得到单行星架轮系机构参数信息图。由图可得各点对应的齿轮节曲线的凸性值、杆长、杆长比参数等信息,为对轮系中心位置和机构尺寸的选取提供指导,以得到满足设计要求的最优行星轮系机构[7-9]。
1 运动学模型建立与计算
1.1 行星轮系机构简化
单行星架轮系机构的运动轨迹C由行星轮上某一点Q的运动所形成,且行星轮轴心与点Q连线的绝对运动为往复摆动,即行星轮的绝对角位移为某一小角度的周期性函数[10-13]。不考虑轮系中传动齿轮的啮合关系,将这类轮系机构简化为二杆二自由度开链机构,并以太阳轮中心为坐标系中心建立参考坐标系,如图1所示。本文运用已知运动轨迹反求机构参数的方法,以给定的平面轨迹所处的坐标系为全局坐标系,在全局坐标系内以轮系中心O1为原点建立参考坐标系和轮系机构简化模型,如图2所示。在全局坐标系中随着轮系中心点位置的变化,可以求解出无数组开链二杆机构实现轨迹再现,每组解对应的杆长和齿轮节曲线形状各不相同。因此,确定轮系中心的位置是求解平面开链二杆机构的关键。

图1 行星轮系机构原理图Fig.1 Schematic of planetary gear mechanism1.行星架 2.太阳轮 3.下中间轮 4.上中间轮 5.行星轮 6.运动臂

图2 开链二杆机构模型Fig.2 Two-link open loop chain mechanism model
图2中Oxy为全局坐标系,O1x1y1为参考坐标系,矩形框为解析区域,O1点为轮系中心,Q点为与行星轮固连的某一点,图1中C为在轮系周转过程中Q点在全局坐标系下形成的运动轨迹。Lo表示在运动过程中轮系中心点O1与Q点的连线长度,La(第1杆)表示轮系的行星架长度,即太阳轮轴心到行星轮轴心的距离,Lb(第2杆)表示行星轮轴心到运动臂尖点Q的距离,L1表示轨迹曲线与轮系中心最近距离,L2表示轨迹曲线与轮系中心最远距离。β1表示x1轴正方向到O1Q1的夹角,β2表示O1Q1到O1B的夹角,θ1表示x1轴正方向到O1B的夹角,θ2表示x1轴正方向到BQ1的夹角。
当轮系中心O1点坐标为(x0,y0)时,行星架La做周转运动,Q从初始位置(x,y)沿给定轨迹移动,行星齿轮轴心B点坐标为(x1,y1)。根据其运动学理论可知,行星轮轴心与点Q连线的绝对运动为在(-π/2, π/2)范围内往复摆动。由图2可知,输入角θ1和输出角θ2计算公式为
θ1=β1+β2
(1)
(2)
行星架做周转运动,在转动过程中不会出现回转的情况,故θ1是周期为2π的单调函数。根据β1、β2的定义可知,β1、β2均为矢量角,β2大小为三角形O1BQ1的内角。当杆La和杆Lb所在直线重合时,即Q处在轨迹曲线上距离轮系中心最远、最近两点。上述参数计算公式为
(3)
(4)
(5)
在单行星架周转轮系机构中,太阳轮与机架固定,行星架匀速转动。假设行星架的转速为nH(即第1杆的转速),行星轮的转速为ni(即第2杆的转速)。单行星架周转轮系机构的总传动比计算公式为
(6)
1.2 非圆齿轮传动比的分配
单行星架轮系机构采用二级齿轮传动,故需要对计算得到的总传动比进行分配。一对非圆齿轮传动要保证主动齿轮转动一周从动齿轮也转动一周,传动比应满足
i=i1i2
(7)

(8)
式中i1——一级齿轮传动比
i2——二级齿轮传动比
1.3 非圆齿轮节曲线凸性判定
假设一对啮合齿轮中主动齿轮为齿轮1,从动齿轮为齿轮2,两齿轮中心距为a。由一对啮合齿轮传动的原理可知传动比i12为
(9)
式中n1——主动齿轮转速
n2——从动齿轮转速
r1——主动齿轮节曲线半径
r2——从动齿轮节曲线半径
当主动齿轮转过φ1时,从动齿轮转角φ2为
(10)
对于一对非圆齿轮传动时,当主动齿轮的转角为φ1时,对应的齿轮传动比为函数i(φ1),在极坐标系中主动齿轮半径为
(11)
封闭非圆齿轮节曲线为全凸形即节曲线的曲率半径为非负数。在极坐标方程中曲线曲率半径ρ的计算公式为
(12)
式中r——齿轮节曲线半径
当主动齿轮节曲线为全凸形时,主动齿轮节曲线曲率半径ρ1≥0。将主动齿轮节曲线半径函数式(11)代入式(12)中可得ρ1为
(13)
由式(11)可得
(14)
(15)
式中i′——传动比曲线的一阶导函数
i″——传动比曲线的二阶导函数
式(14)、(15)代入式(13)中可得
(16)
由式(16)知,主动非圆齿轮为全凸形齿轮时,ρ1≥0。因为式(16)的分子为正数,所以分母
pa=1+i+i″≥0
(17)
式中pa——主动齿轮凸性值
从动齿轮的转角为φ2,在极坐标系中从动齿轮的半径
(18)
从动齿轮节曲线为全凸形时,从动齿轮节曲线曲率半径ρ2≥0。将从动齿轮节曲线半径函数式(18)代入曲率公式(12)中可得ρ2为
(19)
由式(10)可得

(20)
(21)
(22)
式(21)、(22)代入式(19)中可得
(23)
由式(23)可知,从动非圆齿轮为全凸形齿轮时,ρ2≥0。因为齿轮传动比为正数,即分子为正数,所以分母为非负数。
pb=1+i-ii″+i′2≥0
(24)
式中pb——从动齿轮凸性值
将各子级传动比代入式(17)、(24),计算表示非圆齿轮节曲线凸性值pa、pb,越小表明非圆齿轮节曲线上该位置的凸性越差,选取pa、pb较小值表示一对非圆齿轮节曲线凸性。
2 运动轨迹求解与分析
2.1 圆轨迹的求解与分析
在全局坐标系内给定满足设计要求的运动轨迹曲线,并确定轮系中心解析区域范围。设置搜索步长确定计算精度,在解析区域内轮系中心点坐标(x0,y0)按步长递进。在轨迹曲线不变的情况下,轮系中心点的变化使得形成该轨迹的轮系机构参数(杆长La、杆长比、齿轮节曲线凸性值)发生变化。对轮系中心点位于解析区域内各位置点时轮系机构属性进行计算,并将计算结果用杆长等高线、杆长比等高线、齿轮节曲线凸性值等高线表示,绘制单行星架轮系机构属性图,计算过程如下:轮系中心的坐标为(x0+Δx0,y0+Δy0),其中Δx0、Δy0为中心点坐标的变化量即步长,在解析区域内按步长搜索整个目标区域。轨迹方程为f(x,y),轨迹上某点到轮系中心的距离为L。轮系中心点和轨迹曲线最近距离为L1,最远距离为L2。式中轮系中心坐标值已知,轨迹曲线x、y为自变量,有
(25)
(26)
由式(5)可得,轮系中心在该位置点时形成该轨迹的机构杆长和杆长比参数。由式(1)~(6)可计算出机构复演该轨迹两杆转角角位移曲线与轮系总传动比。将总传动比按照运动学原理分配成两级子传动比,并计算由子传动比曲线得到的非圆齿轮节曲线的凸性值。按步长移动轮系中心的坐标重复上述计算过程。将解析区域内轮系中心在各点时的轮系机构参数以La等高线、杆长比等高线、非圆齿轮节曲线凸性值等高线连接,形成单行星架轮系机构参数信息图。
通过分析解析区域内单行星架机构参数信息图,为设计可形成特定轨迹的轮系机构提供参考。以上方法建立了非圆齿轮节曲线形状与运动轨迹之间的直接联系,避免了调试非圆齿轮节曲线的盲目性。另外,解析区域内的单行星架轮系机构参数信息图将指导特定目标运动轨迹的单行星架轮系机构的快速求解,给出了约束条件下最理想的实用解[14-15]。
例如,利用上述求解方法对全局坐标系内的圆形轨迹进行分析计算。计算精度取0.1 mm,解析区域选取(-50 mm,-50 mm)—(50 mm,50 mm)矩形范围进行分析计算,计算结果如图3所示。

图3 圆轨迹单行星架轮系机构参数信息图Fig.3 Parameter information diagram of single planetary gear train mechanism with circular trajectory
从计算结果可知,对于形成圆轨迹的行星轮系机构,其行星架长度La为圆轨迹的半径,与轮系中心位置无关;其传动齿轮组均为圆齿轮且传动比恒为1,节曲线凸性值为2,齿轮节曲线形状与轮系中心位置无关;杆长比随着轮系中心位置不同而变化,随着轮系中心远离轨迹曲线而增大。对于圆齿轮传动的单行星架轮系机构,行星轮上固连点Q形成的轨迹与行星轮中心点形成的轨迹形状相同但位置不同。通过运动学分析可知,传动比恒为1的单行星架轮系机构行星轮绕着太阳轮周转,其齿轮中心点形成的轨迹是以太阳轮中心为原点,以行星架长度为半径的圆。行星轮固连点与齿轮中心距离的变化引起运动轨迹位置的改变。验证了圆轨迹单行星架轮系机构参数信息图求解的正确性。Lb可以通过图中杆长比参数的最优解来确定。设计者可以根据设计需要改变解析区域的范围,进而重新计算单行星架轮系机构参数信息图。
2.2 水稻移栽机构轨迹的计算与分析
常见的水稻移栽轨迹有适用于高速插秧机构的“海豚形”轨迹和“腰子形”轨迹;适用于水稻钵苗移栽机构的“8字形”轨迹和“鹰嘴形”轨迹。为了能得到更好满足农艺要求的水稻移栽机构[16-19],本文对水稻移栽轨迹进行计算分析。
2.2.1高速插秧机构轨迹计算与分析
(1)“海豚形”轨迹
对高速插秧机构的“海豚形”轨迹进行计算,在全局坐标系内给定控制轨迹整体形状的若干型值点(表1),通过三次非均匀B样条拟合求得轨迹曲线如图4a所示。综合轨迹在全局坐标系内的范围和轮系中心点的范围,选取(-80 mm, -30 mm)—(20 mm, 50 mm)为解析区域进行求解,计算结果如图4b所示。
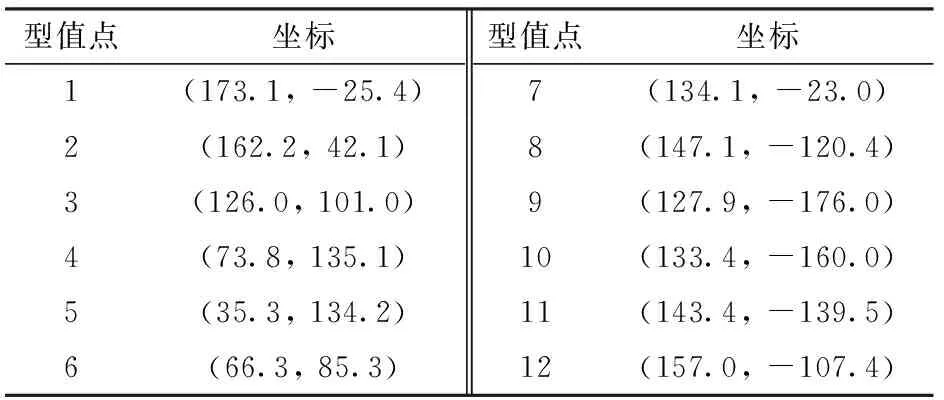
表1 “海豚形”轨迹型值点坐标Tab.1 Dolphin-shaped trajectory point coordinates mm
图4b中杆长La曲线在解析区域内渐变式分布,杆长随轮系中心由上到下逐渐减小;由于轨迹平面形状较为复杂,形成该轨迹的轮系齿轮是非圆齿轮,轮系中心点在不同位置时齿轮节曲线凸性值有很大差别,齿轮节曲线凸性值等高线在解析区域内分布不均匀,解析区域从上到下齿轮节曲线内凹程度迅速增长;杆长比曲线在解析区域内从右上角向左下角逐渐增大。在轮系机构设计过程中,根据齿轮节曲线形状和杆长条件的设计要求,在所需解析区域内寻找约束条件下的最优解[20-21]。

图4 “海豚形”轨迹单行星架轮系机构参数信息图Fig.4 Parameter information diagram of single planetary gear train mechanism with dolphin-shaped trajectory
(2)“腰子形”轨迹
对高速插秧机构的另一种移栽轨迹“腰子形”轨迹进行计算。在全局坐标系内给定控制轨迹整体形状的若干型值点(表2),通过三次非均匀B样条拟合求得轨迹曲线如图5a所示。综合轨迹在全局坐标系内的范围和轮系中心点的范围,选取(-50 mm, -30 mm)—(50 mm, 50 mm)为解析区域进行求解,计算结果如图5b所示。

表2 “腰子形”轨迹型值点坐标Tab.2 Porcine lumbar trajectory point coordinates mm
由计算结果可知,“腰子形”轨迹和“海豚形”轨迹机构参数信息图类似,杆长La、杆长比、非圆齿轮节曲线呈渐变式分布,杆长La随轮系中心由右上到左下逐渐减小;由于轨迹形状与圆轨迹类似,较为简单。轮系中心点在不同位置时齿轮节曲线凸性值差别较小,齿轮节曲线凸性值等高线在解析区域内分布不均匀,解析区域从左上到右下齿轮节曲线内凹程度变大;杆长比曲线在解析区域内从右向左逐渐增大。在轮系机构设计过程中,根据齿轮节曲线形状和杆长条件的设计要求,在所需解析区域内寻找约束条件下的最优解。

图5 “腰子形”轨迹单行星架轮系机构参数信息图Fig.5 Parameter information diagram of single planetary gear train mechanism with porcine lumbar trajectory
2.2.2水稻钵苗移栽机构轨迹计算与分析
(1)“8”字形轨迹
夹苗式行星轮系水稻钵苗移栽机构的移栽轨迹为形状不规则且较为复杂的“8”字形轨迹,取若干型值点如表3所示,利用三次非均匀B样条拟合出“8”字形轨迹曲线如图6a所示。根据实际需要,选取(-30 mm, -30 mm)—(50 mm, 50 mm)为解析区域,求解结果如图6b所示。
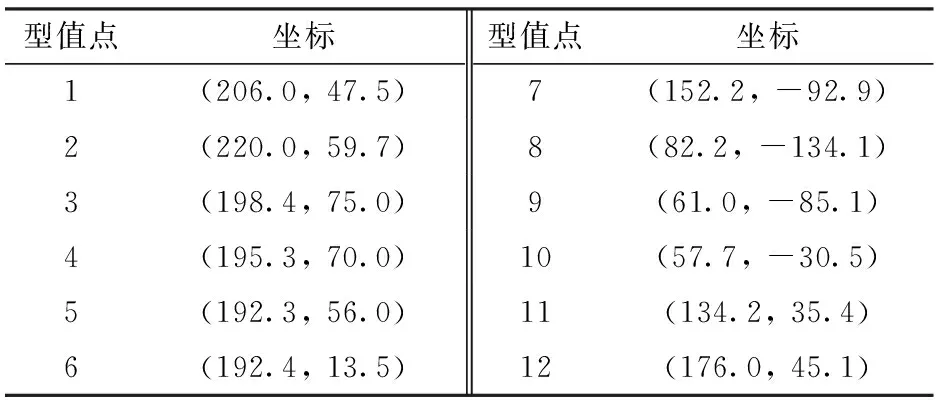
表3 “8”字形轨迹型值点坐标Tab.3 “8” shaped trajectory point coordinates mm

图6 “8”字形轨迹单行星架轮系机构参数信息图Fig.6 Parameter information diagram of single planetary gear train mechanism with “8” shaped trajectory
从图6b可以看出,杆长La曲线在解析区域内呈渐变式分布,杆长随轮系中心位置的变化而变化;因为轨迹平面形状较为复杂,形成该轨迹的轮系齿轮节曲线凸性值比较小即齿轮节曲线内凹,且在解析区域内分布不均匀,解析区域从下到上齿轮节曲线内凹程度迅速增长;杆长比曲线在解析区域内从右下角向左上角逐渐增大。在轮系机构设计过程中,根据设计要求的约束条件在解析区域内寻找最优解。
(2)“鹰嘴形”轨迹
夹土式行星轮系水稻钵苗移栽机构的移栽轨迹为鹰嘴形,取若干型值点如表4所示,利用三次非均匀B样条拟合形成轨迹曲线如图7a所示。根据实际需要,选取(-50 mm, -30 mm)—(30 mm, 20 mm)为解析区域,求解结果如图7b所示。

表4 “鹰嘴形”轨迹型值点坐标Tab.4 Eagle-nosed trajectory point coordinates mm
由图7b可知,杆长La曲线在解析区域内渐变式分布,杆长随轮系中心位置的变化而变化,在解析区域内由上到下逐渐变大;由于鹰嘴形轨迹形状较为复杂,形成该轨迹的轮系齿轮节曲线凸性值比较小,解析区域内轮系中心点在不同位置时齿轮节曲线形状差异较大且内凹较为严重;杆长比曲线在解析区域内从右向左逐渐增大。
从上述实现4种轨迹的单行星架轮系机构参数信息图可以看出,轨迹形状与圆形轨迹越相近,则在解析区域内齿轮节曲线凸性值越接近2,非圆齿轮工作性能越好。如“腰子形”轨迹齿轮节曲线凸性值接近圆齿轮凸性值,近似全凸形齿轮,工作性能优异。“8”字形、“海豚形”、“鹰嘴形”轨迹形状较复杂,形成这类轨迹的轮系在解析区域内齿轮节曲线凸性值差异较大,齿廓存在一定程度的根切。圆轨迹的轮系机构的杆长La与轮系中心位置无关,只与圆轨迹的半径有关;非圆轨迹的杆长La与轮系中心和轨迹的相对位置有关。杆长比与轮系中心在全局坐标系内的位置相关。在设计过程中根据解析区域内轮系机构的参数信息选取轮系中心避免了盲目性,可以达到机构参数的最优化。

图7 鹰嘴形轨迹单行星架轮系机构参数信息图Fig.7 Parameter information diagram of single planetary gear train mechanism with eagle-nosed trajectory

图8 不同轮系中心位置对应机构齿轮节曲线组合Fig.8 Combination of gear pitch curves for each position of planetary gear train mechanism center
2.3 参数信息图的分析
分析图6b所示“8”字形轨迹单行星架轮系机构参数信息图,在解析区域内分别选取轮系中心点为(30 mm, -28 mm)、(25 mm, -25 mm)、(10 mm, -10 mm)、(0, 0)、(5 mm, 5 mm)、(10 mm, 10 mm),计算形成该轨迹的轮系机构总传动比,并对总传动比进行两级分配,得到传动非圆齿轮节曲线形状如图8所示。对比图8a~8f可知,轮系中心位置对非圆齿轮节曲线形状有影响。
La为行星轮中心到太阳轮中心的距离,反映了行星架的尺寸。Lb为运动臂的长度。在设计过程中,设计不同用途的单行星架轮系机构时,由于对尺寸的要求不同,首先在La目标区域内确定轮系机构的参数,可以避免因行星架尺寸不满足设计要求而引起的对定轨迹的多次反求计算。单行星架行星轮系机构一般采用双运动臂布局用以提高工作效率,结构简图如图9所示。O3G1D1、O5G2D2为两个运动臂,轮系周转运动过程中,双臂做摆动运动。当杆长比值过大时,在周转的过程中运动臂G1D1会与G2D2发生干涉。当杆长比大于2时即O3D1的长度大于O3O5时,G1D1在行星架周转过程做摆动运动,会与行星齿轮轴O5发生干涉,影响轮系机构的正常运转。故设计轮系机构时杆长比要小于2。不同功能的单行星架轮系机构运动臂有不同的结构,运动臂固定在行星架的初始角,所需移栽臂的运动轨迹会影响周转过程中双臂的干涉问题。设计者根据实际设计需要考虑G1H1的长度,运动臂初始安装角的大小和运动轨迹的形状,初步确定杆长比范围求解最优机构参数。避免在设计过程中因杆长比过大而产生干涉;或因杆长比过小导致运动臂结构尺寸偏小,从而增加了零件结构设计的难度。本文通过计算解析区域内单行星架轮系机构参数信息图使设计者明确机构的变化趋势,为机构设计时参数的选取提供参考[22-23]。

图9 双臂回转示意图Fig.9 Schematic of double transplanting arm rotation
3 应用实例

根据上述机构参数,进行移栽机构设计、样机加工[24]与试验验证。将移栽机构虚拟样机的仿真轨迹(图11)、试验轨迹(图12)与理论轨迹(图7a)作对比,可以看出仿真轨迹、试验轨迹与理论轨迹基本一致,验证了移栽机构物理样机的正确性,进一步验证了所提出的基于节曲线凸性判别的行星轮系移栽机构求解与分析方法的正确性。

图10 两级非圆齿轮传动节曲线Fig.10 Pitch curves of two stage non-circular gear transmission

图11 仿真轨迹Fig.11 Simulation trajectory

图12 试验轨迹Fig.12 Test trajectory
4 结论
(1)提出了基于节曲线凸性判别的行星轮系移栽机构求解与分析方法,得到了解析区域内单行星架轮系中心在各位置时的杆长La、杆长比、齿轮节曲线凸性值。
(2)通过轮系机构参数信息图的方式为设计者提供参考,避免了正向设计过程中轨迹的不确定性和反向设计过程中轮系中心位置选取的盲目性,有利于设计者明确机构参数在解析区域内的变化趋势。
(3)对水稻移栽的几种常用轨迹进行计算分析,任选一种移栽轨迹进行轮系机构设计。根据轮系机构参数信息图选取轮系中心,并进行虚拟仿真与样机试验。进一步验证了所提出的基于节曲线凸性判别的行星轮系移栽机构求解与分析方法的正确性。该方法简化了轮系机构设计的优化过程,简单实用。
