河南省人口老龄化预测

方萍

（郑州大学，河南郑州450001）

1 引言

当一个区域65岁及以上的老年人口占总人口比重超过10%时，称该国家或地区为老年型社会。而按户籍人口计算，河南省65岁及以上人口占比于1998年开始突破7%，从此进入老年型社会，至2015年65岁及以上人口占比达到9.6%。虽然离老龄社会还有一定的距离，但也需要引起我们的注意。此外河南省的人口结构存在很大的问题，至2013年老年人口的年平均增长率是总人口年平均增长率的2倍有余。因此研究河南省人口老龄化系数的变动趋势，可以为解决河南省人口老龄化问题提供参考。

2 文献综述

人口老龄化问题的研究重点在于人口老龄化系数，根据前人的研究，主要采用以下几类方法对河南省人口老龄化进行研究。一是如郭敬（2015）建立向量自回归模型预测未来几年的人口总数与老年人数，并在此基础上计算相应的人口老龄化系数。二是乔谷阳、乔家君（2016）从空间上对河南省人口老龄化进行分析，以把握其空间分布特征并分析其未来的发展趋势。

虽然以上这些研究方法都具有代表性，但是他们在研究人口老龄化与多种社会经济因素之间的影响上有所欠缺，而应用因子分析则能够很好地解决上述问题。因此本文首先运用因子分析得出影响河南省65岁以上老年人口占比的影响因素，根据分析结果进一步构建多元回归预测模型，并结合灰色GM（1,1）模型预测河南省未来的人口老龄化系数。

3 实证分析

本文采用河南省1989年至2015年的有关数据，包含了河南省65岁及以上人口占总人口比重、河南省人口总数、人口自然增长率、老龄人口抚养系数、城镇人均可支配收入、城镇化率卫生机构数一共7个指标。

其中，河南省65岁及以上人口占总人口比重代表着河南省人口老龄化系数，河南省人口总数与人口自然增长率代表着河南省人口的发展动态，。

而城镇居民人均可支配收入与城镇化率则代表了河南省的社会经济发展程度。当一个区域的城镇化率与人均可支配收入都比较高时，这反映出当地的社会经济发展水平比较高。同样卫生机构数反映的是一个地区的医疗水平，虽然数量不等等同于质量，但较多的卫生机构数量可以保证日常诊治与急救的及时性。

之所以增加河南省老龄人口抚养系数，是因为老龄人口抚养系数可以从经济角度反映人口老化社会后果的指标之一，较低的老龄人口抚养系数表明主要劳动年龄人口的抚养压力比较小，表明老年人都可以得到较好的照顾与生活保障。

3.1 因子分析与指标选取

本文首先采用因子分析法来选取影响人口老龄化的指标。因子分析法有利于从众多的观测指标中选取若干重要指标，用少数独立的观测变量来表示其基本的数据结构，以此来获得各观测指标与所研究的指标之间的相关关系。因子分析可以达到数据简化的目的，因此其应用极为广泛。

如表1所示为运用eviews软件处理后的因子载荷图。从图一我们发现只存在一个主因子，且这一个主因子方差贡献就达到了100%，这表明这一主因子非常好的解释了所有的原始变量，而且6个指标都被包含其中，都有较高的因子载荷。本文选取因子载荷在98%以上的3个指标作为影响因素，分别为城镇化率、老龄人口抚养系数、卫生机构数，以河南省人口老龄化系数为因变量来建立多元线性回归预测模型。

表1 因子载荷表

3.2 多元线性回归预测模型的建立

多元线性回归利用线性来拟合多个自变量和因变量的关系，从而确定多元线性回归模型的参数。如表二所示为根据因子分析结果所选取的3个自变量城镇化率（CZHL）、老龄人口抚养比（LNFYB）、卫生机构数（WSJGS）与因变量人口老龄化系数（65ZB）所构建的多元线性回归模型检验结果。

其中用来表示拟合优度的为调整后的判定系数R方为0.975，这说明有97.5%的影响因素可以由此模型来加以解释，相应的各自变量的系数显著性概率值全都小于0.05，所有的T值均大于临界值T（27-3-1）=2.069，表示结果在α=0.05的水平上是显著的。此外，该回归模型的DW值为1.4，说明随机误差项不存在一阶序列相关；AIC值为-0.63较小意味着滞后阶数较为合适。总体表明所建立的回归模型比较好。

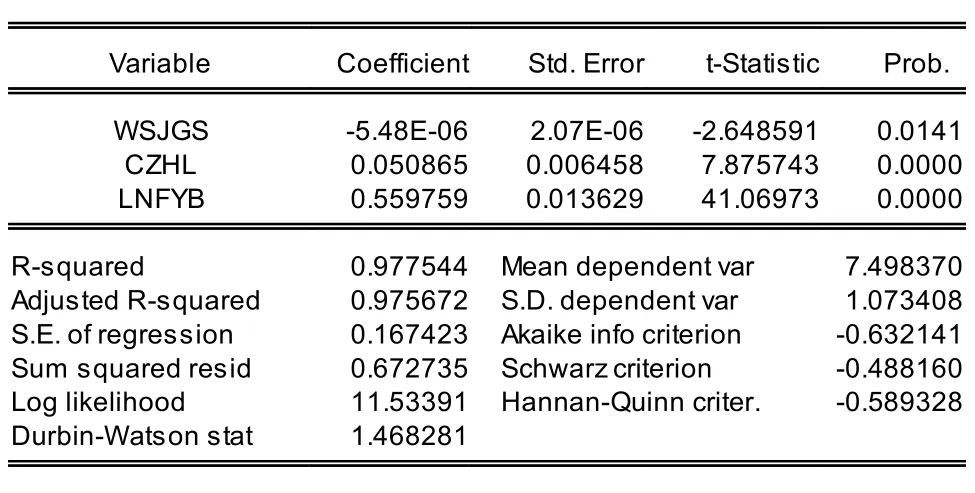
表2 多元回归模型

因此根据表2中的各标准化系数值，得出河南省人口老龄化的多元线性回归方程为：

65ZB=+0.0509*CZHL+0.5598*LNFYB+-5.48404008994e-06*WSJGS

式中65ZB为河南省人口老龄化系数；CZHL为河南省城镇化率；LNFYB表示河南省老龄人口抚养比；WSJGS为河南省卫生机构数。

图1所示的是运用本文的多元回归线性模型所得出的1989年至2015的预测值与实际值的拟合效果。图中蓝线表示河南省65岁及以上人口占总人口比重的实际值，红色表示的是预测值。从图中可以看出所得的预测值与实际值较符合，总体上河南省人口老龄化呈现出波动上升的趋势。

3.3 河南省人口老龄化系数预测

多元线性回归模型虽然可以很好地反映解释变量与被解释变量之间的关系，但使用多元线性回归模型进行预测时，要求所有的解释变量都是已知的。为了能实现对未来的预测，本文选用灰色预测法中的GM(1,1)模型来预测未来5年相关变量的数据。

本文选取河南省1989—2015年城镇化率、老龄人口抚养比和卫生机构数作为原始数据，运用GM(1,1)模型对河南省2016—2020年的城镇化率、老龄人口抚养比和卫生机构数进行预测，将输出结果作为多元线性回归预测方程的输入来计算河南省人口老龄化系数，实现灰色预测模型与多元线性回归方程的有机结合，最终取得较高精度的预测结果。

将河南省2016—2020年的城镇化率、老龄人口抚养比和卫生机构数的预测值代入多元线性回归模型中，就可以得到河南省2016—2020年的人口老龄化系数，预测结果如表3所示。我们可以看出未来河南省人口老龄化系数会不断增大，但每年以0.4%左右的速度上涨，相对来说增幅较小，距离进入老年型社会还有一定的时间。

表3 河南省2016—2020年的人口老龄化系数

4 结论分析

本文将多元线性回归模型理论和灰色系统理论相结合，模型解释能力强、预测精确性高，多元线性回归模型表明人口老龄化系数与城镇化率、老龄人口抚养比和卫生机构数量具有高度相关性，而灰色系统理论则支持多元线性回归模型做中长期预测，摆脱了多元线性回归模型由于缺乏未来的解释变量而不能预测未来的缺点。

从本文所得出的多元线性回归模型中我们可以发现，河南省人口老龄化与城镇化率、老龄人口抚养比和卫生机构数量高度相关。

首先，从人口结构来说，我国现如今实行二胎政策，鼓励生育的政策虽然会扭转老龄化的人口结构，但是会导致河南省青壮年人口赡养负担加重，原因是河南省原本就是人口第一大省，二胎政策增加了新生人口，但老年人口并没有减少。那么所有两端的赡养压力都会集中在中间的劳动年龄人口，这对于河南省广大的工薪阶级而言其实存在非常大的抚养压力。

其次在医疗卫生水平方面，有些研究指出老年人口的平均医疗支出是65岁以下人群的2.7～4.8倍（黄成礼，2004）。那么对于河南省这样一个人口大省来说如何解决“看病难”这一问题需要政府医疗制度的支持。一是社会医疗保障要回归普惠性、合理性和公平性原则，尤其加大政策对贫困人群的医疗报销比例倾斜。二是河南省地域广阔，需要重视基层医疗服务能力，需要通过省内投入和完善人才培训机制来补足基层医疗服务能力短板。

最后，促进一个地区的经济的发展最终是要落实到使广大人民群众受惠。公共财政收入随着经济增长而增长，而社会福利作为公关财政的重要支出，与人口变化的关系尤其紧密。发达国家的政府教育、养老和医疗支出占了各级财政收入的50%以上，对比发达国家，目前河南省在这三方面的支出有所不足，还存在很大的上升空间。伴随着老龄化，可以逐步调整政策规划，以实现河南省人口结构与社会经济的良性发展。