基于神经网络模型计算感潮河段断面平均流速

陈健健，曹贯中

（长江水利委员会长江下游水文水资源勘测局，江苏 南京 210011）

0 引言

长江下游感潮河段同时受上游径流和海洋潮汐 2 种动力作用，以上游来水影响为主，水位、流量呈波浪型变化。适用径流河段的多种流量推求方法均不适用于感潮河段，因此，感潮影响下流量的报汛及整编目前皆处于摸索阶段，这很大程度上制约了水文工作的功效和作用[1]。近年来，声学多普勒流速剖面仪（Acoustic Doppler Current Profiler，ADCP）在全国范围内已普及使用，ADCP 测流具有安装简单、测量精度高、测验成本低等诸多优点；随着 ADCP 在线测流系统的建设，通过实时采集水体流速，利用指标流速法推流成为一种切实可行的方法[2–3]。

已有研究中多通过线性回归方法计算 ADCP 指标流速与断面平均流速之间的函数关系，并取得较好的研究效果[4–5]。为进一步提高拟合精度，可采用神经网络模型。人工神经网络是基于大脑神经网络结构和功能而建立的一种信息系统，属于隐式模型，具备自组织、自适应及自学习功能，具有较强的非线性映射能力等优点[6]。本研究以南京水文实验站 2014 年 5 月—2016 年 12 月 9 次全潮测量为例，研究感潮河段断面平均流量的推求方法在MATLAB 神经网络工具箱中的可行性，并将结果与多元回归分析方法结果进行比较，为进一步提高资料整编精度进行探讨与尝试。

1 神经网络基本原理

1.1 BP 神经网络简介

BP 神经网络是目前应用最为广泛的一种神经网络模型，又称为多层前馈神经网络，能学习和存贮大量的输入—输出模式映射关系。其特点是不仅具有输入层节点、输出层，而且有隐含层，层与层之间采用全互连方式，同一层之间不存在相互连接。隐含层可以有 1 个或多个，每层上的神经元又称为节点或单元[7]。

1.2 神经网络训练策略

为了使实际输出值与网络期望输出值相吻合，可用含有一定数量学习样本的样本集和相应期望输出值的集合来训练网络。训练过程实际上由前向计算和误差反向传播过程组成。在前向计算过程中，输入信息从输入层经隐层逐层计算，并传向输出层，每层神经元的状态只影响下一层神经元的状态。如输出层不能得到期望的输出，则转入误差反向传播过程，误差信号沿原来的连接通路返回，通过修改各层的神经元的权值，使得网络系统误差最小，最终实现网络的实际输出与各自所对应的期望输出接近。确定了网络层数、每层节点数、传递函数、初始权系数、学习算法等也就确定了 BP 网络。

1.2.1 常用的传递函数

BP 网络的传递函数有多种，主要包括：

1）Log-sigmoid 型函数。其输入值可取任意值，输出值在 0～1 之间。

2）tan-sigmod 型函数。其输入值可取任意值，输出值在 -1～1 之间。

3）purelin 型函数。为线性传递函数，其输入与输出值可取任意值。

BP 网络通常有 1 个或多个隐层，该层中的神经元均采用 sigmoid 型传递函数，输出层的神经元则采用线性传递函数，整个网络的输出可以取任意值。

1.2.2 隐含层节点数的确定

对于多层前馈网络来说，隐层节点数的确定是成败的关键。若数量太少，则网络所能获取的用以解决问题的信息太少；若数量太多，不仅增加训练时间，更重要的是隐层节点过多还可能出现所谓“过渡吻合”问题，即测试误差增大导致泛化能力下降，因此合理选择隐层节点数非常重要。一般在能正确反映输入输出关系的基础上，应选用较少的隐层节点数，以使网络结构尽量简单，即先设置较少的节点数，对网络进行训练，并测试学习误差，然后逐渐增加节点数，直到学习误差不再有明显减少为止。

2 工程应用

2.1 工程概况

南京水文实验站地处南京河段，测验河段上、下游较为顺直，横断面形态为偏“V”型，深槽紧靠右岸，左岸为平缓式滩地，右岸为砼护岸防洪墙。断面位于京沪高铁南京长江大桥与南京第三长江大桥中间，断面上游 7 km 处有新潜洲滋长，下游 3 km处有梅子洲横亘江中。断面河床大部分由砂土组成。

南京水文实验站设立于 2004 年，目前开展观测的项目主要有水位、流量、降水、悬沙、悬颗、床颗、水温等。其所处南京河段属于长江下游感潮河段，水位年内变幅较大，每日两涨两落，呈非正规半日潮型。

为了填补长江下游感潮河段流量测验系列资料空白的需要，南京水文实验站 ADCP 在线测流系统于 2014 年 1 月 1 日正式投产，2014—2016 年仅采用 1 套定点垂向 ADCP 和 1 套水平式 ADCP 进行指标流速（vf，vh）的实时监测；其中定点垂向 ADCP位于过水断面中部，起点距（1 595 m）处用以监测该垂线的垂线平均流速 vf；水平式 ADCP 安装在右岸陡坡，最长监测距离近 300 m，用以监测区段水平层水平平均流速 vh，如图 1 所示。

图 1 南京水文实验站在线测流系统布置图

此次工程实例采用的数据为 2014 年 5 月—2016 年 12 月 9 次全潮水文测验数据，涵盖不同流量级（-3 145～78 804 m3/s）大中小潮，监测断面平均流速 259 次，指标流速选择 vf，vh。

2.2 MATLAB 神经网络模拟过程

神经网络工具箱是在 MATLAB 环境下开发出来的许多工具箱之一。它以人工神经网络理论为基础，利用 MATLAB 编程语言构造出许多经典神经网络的激活函数，比如 S 型、线性、竞争层、饱和线性等激活函数，使设计者对所选定网络输出的计算，转变为对激活函数的调用。以下主要利用MATLAB 神经网络工具箱中 nftool 模块实现 ADCP指标流速对断面平均流速的拟合。

需要输入网络模型的输入值和目标值。以只考虑垂线平均流速 vf的单一指标为例对模型建立和求解进行说明。在有监督的机器学习中，数据集常被分成 3 个，即：训练集、验证集、测试集。其中训练集用来估计模型，验证集用来确定网络结构或者控制模型复杂程度的参数，而测试集则检验最终选择最优的模型的性能如何。3 个部分都是从样本中随机抽取的。

本次模型选取的全潮监测频数共计 259 次，其中 70%（即 181 次）作为训练集，15%（39 次）作为验证集，15%（39 次）作为测试集。

下一步需要确定隐含层中神经元的个数。训练一个单隐层的 3 层 BP 网络，可根据如下经验公式选择隐层节点数：

式中：k 为隐含层节点个数，n 为输入节点个数，m为输出节点个数，a 为 0～10 之间的常数。选入的指标流速种类数即为输入节点个数，如只考虑单指标流速时，输入节点个数 n 等于 1，当考虑 2 个指标流速时，n 等于 2；输出为实测断面平均流速，因此输出节点个数为 1。因此，根据式（1），隐含层节点个数 k 可取 2～12。以下主要针对 k 取值范围为2～10 进行试算，从而获得最优方案。

建立了 ADCP 指标流速对断面平均流速拟合的神经网络模型，然后即可对网络进行训练，并获得相应参数和结果。需要指出的是，使用 MATLAB 神经网络工具箱图形用户界面时，其初始权值等由软件随机给出，对于本模型相对较为简单，因此初始值对模型计算效率影响不大，因此可不特别设定初始值。训练结果界面如图 2～3 所示。

训练迭代共进行了 26 次。结果显示，训练集拟合结果与实测值间的相关系数达到 0.994 53，验证集达到了 0.996 10，测试集达到了 0.990 34，所有数据（即 2014 年 5 月—2016 年 12 月共 259 次）计算获得的拟合值与实测值间的相关系数达到了 0.994 19。

需要指出的是，由于训练集、验证集和测试集为随机选取，因此即使对于相同数据，但每次求解时，获得的参数及结果也会有所不同。

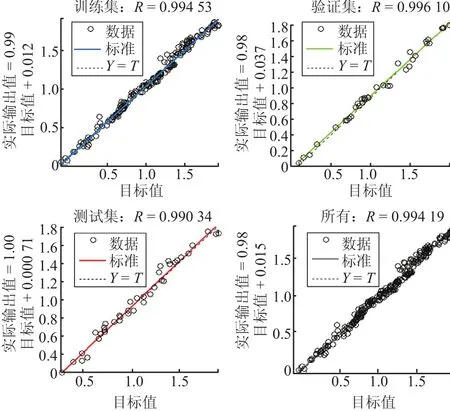
图 2 不同数据集的相关系数

图 3 均方误差随迭代次数的变化

2.3 计算结果与讨论

建立 2014 年 5 月—2016 年 12 月 9 次全潮期间指标流速与实测断面平均流速间的神经网络模型，主要考虑以下 3 种组合方案情况：

1）只考虑垂线平均流速 vf1与断面平均流速 v之间的关系；

2）只考虑水平平均流速 vh与断面平均流速 v之间的关系；

3）综合考虑垂线平均流速 vf1、水平平均流速vh与断面平均流速 v 之间的关系。

计算获得以上时段内不同隐含层节点数情形下所有数据集的相关系数 R 如表 1 所示。

表 1 不同隐含层节点数对应所有数据集的相关系数

由表 1 可以看出：

1）BP 神经网络模型中隐含层数为 1 层时，即可实现较好的拟合精度。

2）总体上看隐含层节点数的增加对所有数据集拟合精度的影响不大，即使隐含层节点数相对较少时，拟合精度也相对较高；并且随着隐含层节点数的增加，拟合精度未随之增大，局部个别情况有所波动，这主要是由于训练集是随机选取的缘故。

3）由于隐含层节点数为 2 时，3 种方案拟合值与实测值间的相关系数皆达到了 0.98 以上，已满足精度要求，同时，相应参数较少，模型较为简单，因此在实际应用时可选用隐含层节点数为 2 的神经网络模型。

为更直观地比较不同方案下回归模型与神经网络模型的精度，可通过多元线性回归模型对以上3 种方案进行计算，计算结果如表 2 所示。

表 2 不同方案回归模型结果

比较表 1 和 2 可以看出：

1）2 种模型拟合精度皆很高，神经网络模型拟合精度总体上略好于多元线性回归模型的拟合结果，各方案下相关系数皆 ＞ 0.98，特别是方案 3 下的相关系数值皆 ＞ 0.99，说明 2 种模型都能达到很好的拟合效果。

2）神经网络模型的拟合精度略好于多元线性回归分析的，尤其是对于方案 1 和 2 只考虑单一指标流速时，可在原有较高精度的基础上再有所提高。

3 结语

本研究主要通过 MATLAB 神经网络工具箱中的nftool 模块实现 ADCP 指标流速对断面平均流速的拟合，拟合精度较高，尤其是对于只采用单一指标流速而言，其拟合效果要略好于多元线性回归模型。同时，采用神经网络工具箱图形化界面具有直观、便捷、易于操作等特点，但也存在参数初始值无法特别设定、拓展性较差等缺点。可通过 MATLAB 特有的 M 文件有效弥补，编写好的 M 文件经过编译后可被其它语言调用进行混合编程，从而实现在线实时分析。因此，该方法在基于 ADCP 指标流速计算感潮河段断面平均流速的研究中具有较好的应用前景。