缤纷“视”界 精彩纷呈
2019-01-03吴晓刚
吴晓刚
“空间观念”是新课标中凸显的十大核心理念之一,考查同学们根据物体特征抽象出几何图形,或根据几何图形想象出所描述的实际物体的能力。三视图很好地承载了这种理念,也为同学们将来学习高中立体几何做铺垫。下面吴老师就带领同学们一起走进中考试卷中缤纷的“视图”世界。
一、由立体图形得三视图
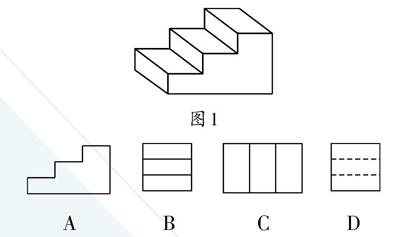
例1 (2019·扬州)如图1所示,物体的左视图是()。
图1
AB C D
【解析】左视图是从左面看到的图形。本题中的物体从左边看到的是一个矩形,由于中间还有两条看得见的轮廓分割线,所以矩形的中间有两条实线。故答案为B。
【点评】主视图、左视圖、俯视图是分别从物体正面、左面和上面看所得到的图形。解答此类问题时要注意题目要求,并且还要注意几何体是否有被挡住的部分,以确定轮廓线的虚实。
二、由三视图得立体图形
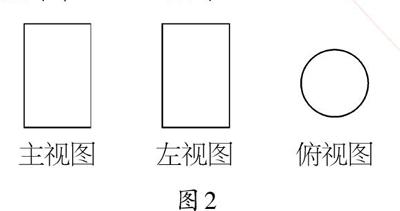
例2 (2019·常州)如图2是某几何体的三视图,该几何体是()。
A.圆柱 B.正方体
C.圆锥 D.球
图2
【解析】根据该几何体的主视图和左视图是长方形,可判断出该几何体为柱体。再根据俯视图是圆,可知该几何体是圆柱。
【点评】由视图描述几何体的过程是根据视图想象出空间形状和结构的过程,需运用逆向思维,需要同学们加强空间想象能力的培养。当同学们对一些常见几何体的三视图比较熟悉的时候,就能很自然地实现二维到三维的转换,这也是一种较高数学素养的体现。
三、与三视图有关的计算
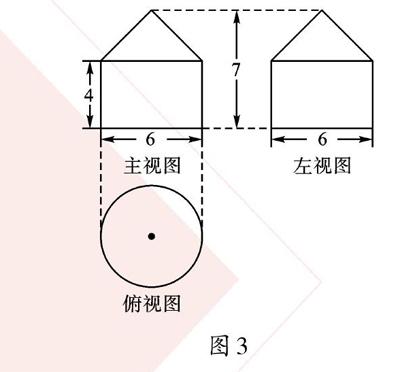
例3 (2019·大庆)一个“粮仓”的三视图如图3所示(单位:m),则它的体积是()。
A.21πm3B.30πm3
C.45πm3D.63πm3
图3
【解析】由“粮仓”的三视图可知该几何体为圆柱和圆锥的组合体。圆柱和圆锥的底面圆直径同为6m,高分别为4m和3m,所以该几何体的体积为:32π×4+[13]×32π×3=45πm3。
【点评】本题考查了三视图的主要性质,“主俯长对正,主左高平齐,俯左宽相等”。根据这条性质可以得到几何体的长、宽、高,即本题中的直径和高,这是解决此类题的要点。
四、搭小正方体与三视图
例4 (2019·宜宾)已知一个组合体是由几个相同的正方体叠合在一起组成的,该组合体的主视图与俯视图如图4所示,则该组合体中正方体的个数最多有()个。
A.10 B.9C.8D.7
图4
【解析】借助所给俯视图来搭小正方体。先根据主视图分析得出每列小正方体的最高层数从左往右依次为2、2、1,再由此确定每个位置的具体个数。该组合体中正方体的个数最多的具体搭法如图5所示,故答案为2+2+2+2+1=9。
图5 图6
图7 图8
【点评】“三缺一”是“搭小正方体”与三视图问题中的经典题型,解题策略是抓住三视图的基本性质,由主视图可得几何体的长和高,由左视图可得几何体的高和宽,由俯视图可得几何体的长和宽。解题要点是抓住俯视图进行搭建,再由主视图分析出每列中的小正方体的最多个数,由左视图分析出每行中的小正方体的最多个数。
本题也可以求出小正方体的最少个数,只要保证每行每列中有一处是最多个数,其他都为最少的1个即可,例如图6的搭法。
若已知左视图和俯视图,求法类似;而若已知主视图和左视图,则挑战性就比较大了,因为缺少俯视图,解题就缺少抓手,需先分析出俯视图。如本题,将条件中的俯视图改为左视图,则根据主视图可得几何体的长为3个单位,根据左视图可得几何体的宽为3个单位,由此得到图7所示的俯视图,再由上面的方法可得小正方体的个数最多的搭法,如图8所示。
(作者单位:江苏省南菁高级中学实验学校)
