一种新型烹饪并联机器人位置与工作空间分析

杨世明 马庆国 郭翠敏

(天津工业大学机械工程学院，天津 300387)

目前中国的烹饪过程主要依靠人工来完成[1-2]，由于个人烹饪水平的不同，烹饪工艺也很难实现一致性，因此市场和家庭迫切需要一款能完成烹饪工艺的烹饪机器人，将烹饪工艺规范化[3-4]、统一化。

目前国内外的烹饪机器人只能实现简单的搅拌，味道不能够保证，文献[5]提到的自动烹饪锅解决了烹饪的自动化问题，但不能实现炒、熘等中国烹饪工艺的核心技法。文献[6]中提到烹饪并联机器人实现了专业厨师动作要求，但由于自由度少，能实现的锅具运动有限。专利[7]中提到的自动炒菜机伺服机械装置，是可对菜肴进行多种操作加工的装置，但却未具备物料的自动投放以及中餐核心烹饪工艺过程如划油、晃锅、翻锅等功能。

针对目前烹饪机器人存在的问题，结合烹饪工艺将人工烹饪动作进行分解，最终设计了2RRPS/SPS并联机构作为自动烹饪机器人工作平台，并对其进行位置分析和工作空间研究[8-11]。以期最大程度地模仿人工烹饪动作，保证美味可口的同时人力，有利于烹饪工艺规范化发展。

1 烹饪机器人工作平台

1.1 工作原理

人工烹饪过程中锅具的运动轨迹较为复杂，锅具的运动方向、速度、加速度等特性直接影响着菜肴制作的质量。本研究选取几种最常见的锅具运动轨迹[12-14]作为烹饪机器人工作平台的运动要求。

(1) 旋锅运动[图1(a)]：工作平台做圆周运动，目的是使食物与锅壁产生相对滑动，防止黏锅。

(2) 颠锅运动[图1(b)]：工作平台做前后摆动和上抛的复合运动，目的是使食物翻转，搅拌均匀，防止粘锅和使食物受热均匀。

图1 自动烹饪机器人工作平台工作原理

(3) 翻锅运动[图1(c)]：工作平台轴线绕定轴做旋转运动的同时绕轴线做小幅摆动，目的是使食物沿着锅壁旋转，受热均匀。

(4) 倾斜运动[图1(d)]：工作平台绕水平轴线做旋转运动，目的是使食物倒出。

1.2 工作平台的设计

根据锅具运动轨迹要求，烹饪机器人工作平台需要实现3个方向移动和转动。为最大程度模仿人工烹饪动作，实现以上运动轨迹，设计了一个具有6自由度的2RRPS/SPS新型并联机构作为烹饪机器人的工作平台(图2)。2条结构相同的RRPS支链和1条SPS支链沿周向均布在定平台(下)和动平台(上)之间。文中的R、P、S分别表示转动副、移动副、球面副。其中转动副R1的轴线与定平台垂直，移动副P1和转动副R2轴线垂直，转动副R2轴线和转动副R1轴线垂直。

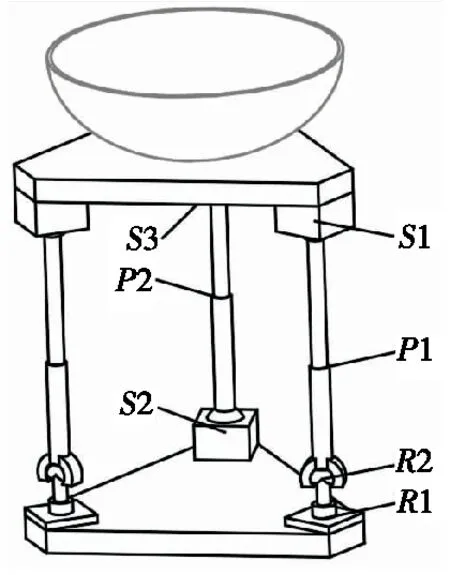
图2 烹饪机器人工作平台

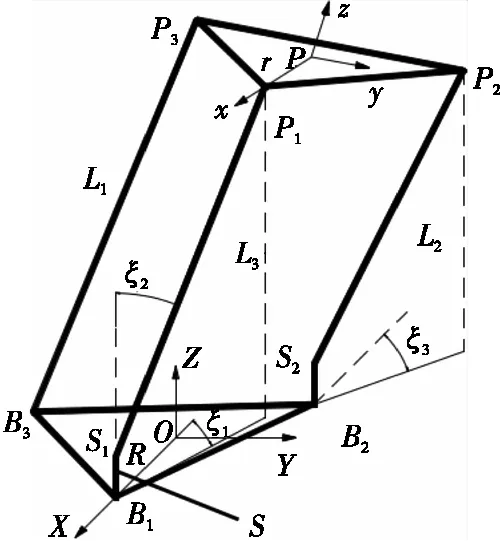
图3 2RRPS/SPS新型并联机构坐标系简图

2 工作平台位置分析

2.1 位置反解

已知动平台的位姿，求解驱动件的位置称为机构的反解[15-17]。目前，并联机构位置分析的主要方法有数值法[18-20]和解析法[20-23]。数值法的优点是建立数学模型简单，没有繁琐的数学推导，可求解任何并联机构，缺点是计算量大，速度慢且迭代结果有可能发散，很难求得机构的所有位置解。解析法的优点是不需要初值并且可以求得全部解，能避免奇异问题，缺点是数学推导极为复杂。结合烹饪机器人工作平台的空间结构分布，运用解析几何法，对其进行位置反解。

已知动平台位姿α、β、γ、OXP、OYP、OZP，求3个驱动杆长度(L1、L2、L3)和3个驱动轴角度(ξ1、ξ2、ξ3)。根据已知条件和机构几何关系，可求出P1、P2、P3在动坐标系中的坐标值PP1、PP2、PP3[式(2)]，通过姿态变换矩阵T[式(3)]可进一步求得P1、P2、P3在定坐标系中的坐标值OPi(i=1,2,3)，即：

OPi=T[PPi1]，

(1)

(2)

(3)

Sα=sinα;Cα=cosα;Sβ=sinβ;Cβ=cosβ;Sγ=sinγ;Cγ=cosγ。

根据烹饪机器人工作平台给定的结构尺寸，可列出驱动杆和驱动轴与OPi间的关系，即：

(4)

(5)

(6)

L2=

(7)

(8)

(9)

式中：

OXPi、OYPi、OZPi(i=1,2,3)分别为式(1)中求得的Pi点在定坐标系中X、Y、Z方向的坐标值。

式(4)～(9)为6个驱动件的变化规律，利用式(4)～(9)对该工作平台进行反解，可以得到3个驱动杆杆长和3个驱动轴转角。

2.2 位置正解

已知并联机构驱动件的位置参数，求解输出件的位姿称为机构的正解。在已知L1、ξ1、ξ2时，根据该工作平台的几何关系，可求出P1点在定坐标系中的坐标值OP1，即：

(10)

P1位置确定后，根据给定的驱动件的位置参数(L2、ξ3)和几何关系，可求出P2点在定坐标系中的坐标值OP2，即：

(11)

同理，可求出P3点在定坐标系中的坐标值OP3，即：

(12)

P1、P2、P3点位置确定，则动平台的位姿已确定，其中动平台中心点P的坐标为：

(13)

3 算例

如图2，设R=r=500 mm，s=50 mm，运用Matlab软件编程，对烹饪机器人工作平台进行位置正反解和运动仿真。表1为工作平台的反解计算结果；表2为工作平台的正解计算结果。表2中的5组正解与表1中的5组反解相比，有微小误差，这主要是由于表2中的驱动件参数为近似值所引起的，正反解结果总体上相互吻合，从而验证了正反解表达式的正确性。这5组解对应的工作平台位置见图4。

将对锅具的4种基本运动进行运动仿真：

(1) 旋锅运动：令L1=L2=800 mm，L3=843.672 mm，ξ1=ξ3=0°，ξ2=π/6，给烹饪机器人工作平台的驱动轴ξ1、ξ3施加相同角速度，其他驱动件保持不变进行仿真(图5)，检测动平台中心点的运动轨迹，同时动平台平行于XOY平面。

表1 反解计算结果

表2 正解计算结果

图4 工作平台位置图

图5 旋锅运动

(2) 颠锅运动：令L1=L2=L3-50=800 mm，ξ1=ξ2=ξ3=0，给烹饪机器人工作平台的驱动杆L1、L2、L3施加线速度(其中ν1<ν2=ν3)，同时对驱动轴ξ2施加角速度，其他驱动件保持不变进行仿真(如图6所示)，检测动平台中心点的位置和运动轨迹以及动平台在做运动时的5个位置。

图6 颠锅运动

(3) 翻锅运动：令L1=L2=800 mm，L3=950 mm；ξ1=ξ2=ξ3=0，令烹饪机器人工作平台的驱动杆L1、L2、L3依次伸缩，其他驱动件保持不变进行仿真(图7)，检测动平台的位置和P1、P2、P3运动轨迹。

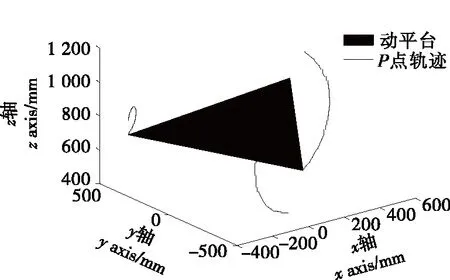
图7 翻锅运动

(4) 倾斜运动：令L1=L2=L3-50=800 mm，ξ1=ξ2=ξ3=0，给烹饪机器人工作平台的驱动杆L1均匀线速度，其他驱动件保持不变进行仿真(如图8所示)，检测动平台中心点的位置和运动轨迹以及动平台在运动时的5个位置。

图8 倾斜运动

以上4种运动仿真与设定的4种锅具运动轨迹吻合，可以达到预期效果，验证了该烹饪机器人工作平台的有效性。

4 定姿态工作空间分析

烹饪机器人工作平台的设计主要是为了更好地拟合人工烹饪动作实现各种锅具运动，因此运动轨迹的优劣对烹饪机器人的质量有关键性的影响。

影响烹饪机器人工作平台的工作空间因素[24-27]有：转动副的转角范围、主动杆的运动行程、连杆的干涉。综合以上3条影响因素，给定姿态角α=β=γ=0°，750 mm≤L1=L2≤1 250 mm，0 mm

给定姿态角α=γ=0°，β=15°，750 mm≤L1=L2≤1 250 mm，0 mm≤L3≤1 300 mm，检测动平台中心点的空间边界图和该点所能达到的所有位置(图10)。与图9相比，工作平台的工作空间明显缩小，同时整体向X轴负方向偏移，求得OXP、OYP、OZP取值范围分别为-1 069.5 mm≤OXP≤617.5 mm，-873.28 mm≤OYP≤873.28 mm，929.84 mm≤OZP≤1 235.24 mm。

由图9、10可知，烹饪机器人工作平台有较大的工作空间，工作空间边界光滑且内部没有空洞，为后期工作平台运动轨迹的优化提供了理论基础。

图9 定姿态工作空间

5 结论

提出一种基于并联机构的烹饪机器人工作平台，该平台能实现旋锅、翻锅、颠锅、倾斜等人工烹饪时的运动轨迹。运用解析几何法对该工作平台进行了位置分析，给出了该工作平台的位置反解表达式和位置正解表达式；通过MATLAB软件进行了位置正反解验证，通过运动仿真，验证了该烹饪机器人工作平台的有效性；对工作平台进行位姿下工作空间分析，得到该工作平台的这个范围，为后期运动轨迹优化提供了理论依据。