基于神经网络的风电短期功率预测模型研究

2019-01-03宿凤明孙财新李端开

节能技术 2018年6期

宿凤明,孙财新,李端开

(国家电投集团电站运营技术(北京)有限公司，北京 102209)

0 引言

风电场输出功率的波动对电网运行影响较大，准确的短期风电场功率预测能够帮助电网合理制定调度计划，保证电能质量，减少系统的备用容量，降低电力系统运行成本[1]。但由于风资源具有很强的随机性、不稳定性和间歇性，精准的风电场短期输出功率预测具有一定难度。

近些年对短期风功率预测研究的多集中于统计方法，其包含时间序列法[2-3]、持续法[4]、卡尔曼滤波法[5]、混合模型[6-7]以及神经网络方法[8-11]。其中神经网络法基于数据驱动，不必关心输入输出之间的联系，学习大量的输入输出模式映射关系，从而达到需要的预测结果。

理论上来讲，神经网络方法可以进行准确的预测，因而近些年有很多使用机器学习方法预测风功率的研究。但是，神经网络预测的精度受到输入参数、神经元数量、目标函数、激活函数、训练方式等因素的影响，因而近些年部分研究者将精力投入到提高预测精度上来。文献 [12] 为提高精神网络预测精度，应用粒子群优化算法来改进神经网络的预测模型，经过与未改进的模型计算结果相比，改进的预测精度更高；文献[13]在BP神经网络的基础上研究了径向神经网络进行微电网的风功率预测，并取得有效的改进。这些方法主要是基于训练方式、网络结构的优化，并未提及实际神经网络训练过程中比较有效的是输入参数、激活函数、目标函数在风功率预测中的选择与优化。同时，神经网络各个因素间关联紧密，基于一个因素进行神经网络预测精度的改进较为有限。

基于此，本文通过分析输入参数、选择激活函数、目标函数、训练更新方式，经过合适的数据预处理后进行短期分功率预测，后由河南某风场的实测数据进行计算及结果分析。

1 研究方法

本文采用三层神经网络结构，采用梯度下降算法学习优化，反向传播方式调整权值和阈值，选取交叉信息熵作为目标函数，采用sigmoid函数作为激活函数。三层神经网络的输入层的输入节点与输入变量数量相同，只有1个输出节点。隐藏层节点个数参考文献[14]研究结果，采用2N+1个隐藏节点，其中N为输入节点。

1.1 模型建立

将选定数据预处理后的数据作为神经网络的输入值，输入层、隐藏层、输出层的每层输入输出关系为

(1)

式中ai——第i个神经元的输出;

zi——第i的神经元的计算结果;

wij——本层第i个神经元与第j个输入的连接权值;

xj——本神经元的第j个输入;

bi——第i个神经元的偏差值;

由于运用sigmoid函数作为激活函数时，使用平方误差函数作为目标函数会在sigmoid函数计算结果接近于1和0时发生饱和，为提高收敛速率本文选用交叉信息熵作为目标函数

(2)

式中a——某神经元计算输出;

y——某神经元实际输出;

c——目标函数;

n——神经元输出个数;

i——第i个神经元输出。

则某神经元目标函数相对于权重和阈值的偏导数为

(3)

(4)

神经元权重与节点更新如下

(5)

(6)

式中w′——更新后的权重;

w——更新前的权重;

b′——更新后的偏差值;

b——更新前的偏差值;

η——学习率;

x——神经元输入。

由此可见，交叉信息熵作为目标函数时权重和阈值学习的快慢取决于a-y即输出误差，误差大时，其更新多学习速率快，误差小时，学习较慢。

1.2 参数选取

风力发电机组从风轮吸收的功率为[15-16]

(7)

式中p——输出功率;

V——风速;

ρ——空气密度，其主要影响因素为环境的温度与压力;

A——扫风面积，其主要影响因素由风电机组叶片半径、来风风向以及风电机组偏航角度，其中叶片半径为固定值;

cp——风机风能利用系数的影响因素。

风电机组一般控制偏航角度跟踪来风风向，以使其时刻正面迎风。在实际运行过程中，风电机组很难实现准确对风且各风电机组具有一定的随机性。这是由于：(1)机舱、测风塔测量仪表的测量存在误差随应用时间增大而出现偏差；(2)风电机组本身控制系统存在差异，在偏航系统跟踪来风风向时存在一定的差异；(3)偏航系统的动作存在一定的滞后，难以完全实现实时跟踪，在风况复杂时对风具有一定的随机性。

对于变浆距风电机组，cp是关于桨距角β的函数，在一定的叶尖速比下，β=0°时cp值最大，随着桨距角β逐渐增大cp明显地减小。浆距角β对风电机组输出功率的影响主要体现在风力发电机组的最大风能追踪区、恒转速区、恒功率区三种运行工况中。最大风能追踪区风速处于切入风速以上，发电机未达到额定转速，要求浆距角β=0°以实行最大风能追踪控制的变速运行。恒转速区发电机已达到额定转速而风速未达到额定值，随风速上升功率仍增大，此时对转速进行控制而桨距角β仍为零。恒功率区时风速达到额定风速，随着风速的增大，需在转速控制的基础上增加功率控制，调节桨距角β，使输出功率不超过额定值。由此可见，浆距角的控制对数据功率影响较大。同时在实际风电机组运行过程中上述对浆距角要求的实现有一定的差异。其主要原因是：(1)风电机组叶片在安装时很难保证角度完全准确，且各风电机组的安装差异具有随机性，该种情况导致在各种工况下风机输出功率均有一定偏差，且该偏差具有个性化和随机性的特点；(2)风电机组在控制浆距角跟踪时，其控制执行具有一定的滞后，致使在风况复杂的时候其很难按照上述控制要求跟踪。

由上述分析可知，风功率输出受风速影响最大，预测时风速必须计入；环境温度、压力影响空气密度，预测时应计入；来流风速和风机的偏航角度直接反应风机的对风状况，对功率输出影响较大，预测时应计入；风机的浆距角反应了同一风速下风机的风能利用能力，对功率输出也具有较大影响应计入。

为验证上述分析，本文将设计三种情况来研究风机本身因素对功率预测的影响：

(1)仅考虑风资源参数：风速、风向、温度等；(2)考虑风资源参数和偏航角度：风速、风向、温度、偏航角度等；(3)考虑风资源参数、偏航角度和浆距角：风速、风向、温度、机舱角度、浆距角等。

1.3 数据预处理

为提高神经网络的学习效率、学习精度，防止部分神经元的过饱和，需对获取的数据进行预处理，剔除空缺值、坏值等错误数据，进行数据的归一化。其中风向、偏航等归一化通过分别取正弦值和余弦值，换算到[-1，1]区间；风向、温度等的归一化采用最大最小值方式[17]。

1.4 精度评价

预测的结果评价采用标准均方根误差NRMSE(Normalized Root Mean Square Error)和平均绝对误差MAE(Mean Absolute Error)两个指标[18]

(8)

(9)

式中ppre——风场功率预测值;

ptru——风场功率实际测量值;

pe——所有预测风机的额定功率;

n——预测数据的个数。

2 研究结果

本研究以河南某风场10台1.5 MW风机为研究对象。河南是北方冷空气南下和夏季风北上的通道，冷暖气团的交替会呈现季风气候的特征，季节性变化规律较明显，春季普遍多大风且风况复杂[19]。因此选取2016年1～3月共3个月的数据进行研究，其中1月、2月的数据用于学习，3月数据用于预测。

本研究设计的三种情况来分析各因素对功率预测的影响。

(1)仅考虑风资源参数，即风速、风向、温度等参数。根据建立的模型，导入参数计算后，其曲线预测结果如图1所示;

图1 仅包含风资源参数预测图

(2)考虑风资源参数和偏航角度影响：即风速、风向、温度、机舱角度等参数,曲线预测结果如图2所示;

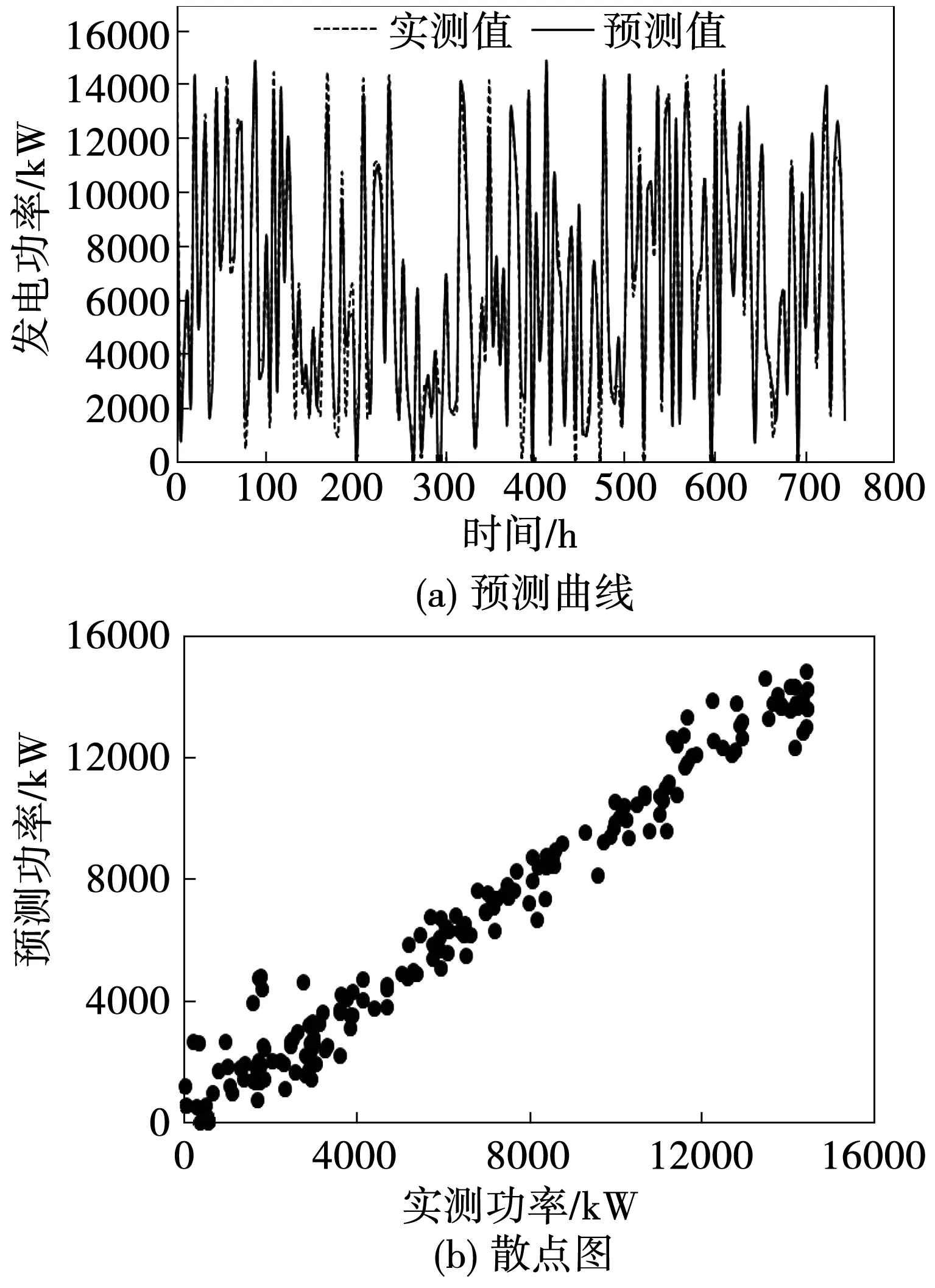
图2 含风资源参数、偏航角度参数预测图

(3)考虑风资源参数、偏航角度和浆距角的影响，即风速、风向、温度、机舱角度、浆距角等参数,曲线预测结果如图3所示。

图3 含风资源参数、偏航角度、浆距角等参数预测图

对比三个预测曲线可以得出：从预测模拟曲线与实际发电量的拟合度上，含有风资源参数、偏航角度和浆距角三个方面参数的预测结果比含有风资源参数和偏航角度两方面参数的预测结果要好，含有风资源参数和偏航角度两方面参数的预测结果要比只考虑风资源参数的预测结果要好。

对比三个散点图可以得出：从预测功率值与实测功率值的线性关系上，含有风资源参数、偏航角度和浆距角三个方面参数的预测结果值好于仅包含风资源参数的预测结果，但风资源参数、偏航角度和浆距角三个方面参数的预测结果与含有风资源参数和偏航角度预测结果相差不大。从离散度上看，含有风资源参数、偏航角度和浆距角三个方面参数的预测结果比含有风资源参数和偏航角度两方面参数的预测结果要好，含有风资源参数和偏航角度两方面参数的预测结果要比只考虑风资源参数的预测结果要好。

由于在使用神经网络进行预测时，除了选用合适的激活函数、使用合适的目标函数、使用合适的优化函数等方法提高预测精度外，选择独立、与预测结果具有相关性的输入参数也是提高预测精度的主要方法之一。在本研究中，(1)由于偏航系统在实际运行过程中，不同风机在同一风向时可能存在不同的迎风角度，继而导致其发电量不同，在神经网络的输入参数中计入偏航角度后，使神经网络在进行学习的过程中将风机在实际运行过程中由迎风角度不同引起的发电量偏差考虑入内，从而提高精度。(2)由于不同的风机在同一风速下，可能存在不同的浆距角而导致发电量不同，在神经网络的输入参数中计入浆距角后，使神经网络的学习考虑了风场内风机在实际运行过程中该部分差异，从而使得这些因素导致的发电量影响也被神经网络学习到，从而提高精度。

经计算，三种情况的NRMSE、MAE整体预测结果如表1所示。

可以看出，仅使用风资源参数计算时的NRMSE和MAE均为最大， NRMSE约为8.58%，MAE超过900 kW；包含风资源参数、偏航角度时的NRMSE和MAE居中，其NRMSE为5.99%，较仅含风资源参数时下降16.7%，MAE约为650 kW，相较下降28.3%；包含了资源、偏航、变浆等参数的情况精度最高，其NRMSE仅有3.20%，较仅含风资源时下降62.7%，MAE小于360 kW，较仅含风资源时下降60.6%。

表1三种情况误差统计对比表

模型NRMSE/[%]MAE/kW仅包含风资源参数8.58909.42含风资源参数、偏航角度参数5.99651.79含风资源参数、偏航角度、浆距角等参数3.20357.82

本研究与文献[8]的研究进行了对比，文献[8]是在输入参数为风速、风向正弦和余弦值以及温度，采用三层网络结构，隐层节点数为2N+1，采用两个月数据预测得到的NRMSE为7.93%，与本研究在仅包含风资源参数且网络结构相同的情况下所得的NRMSE为8.58%与之相近，但本研究在考虑偏航角度和浆距角等参数后的预测结果明显优于文献[8]的预测结果。主要原因如上所述，本文方法在预测时考虑了风机在实际运行过程中偏航角和浆距角的影响。