面向云制造资源的优化配置方法研究*
2019-01-03周临震刘德仿李春燕
殷 亮,周临震,刘德仿,李春燕
(1.盐城工学院 机械工程学院,江苏 盐城 224051;2.江苏大学 机械工程学院,江苏 镇江 212013)
0 引言
云制造是一种基于网络和面向服务的新型网络化智能制造模式,该模式将现代网络化制造技术和物联网、云安全和云计算等技术相融合,对各种制造资源、制造数据和知识进行虚拟化处理,实现对制造资源的统一管理与调度,为企业提供生命周期过程的相关制造资源服务[1-2]。云制造体现了“分散制造资源的集中管理与共享”,能够充分利用闲置的制造加工资源,极大的提高了生产制造的效率[3]。而制造资源的优化配置是云制造技术的核心问题之一,是针对制造要求配置出多个制造服务进行组合来满足制造任务需求。而优化配置模型与对模型的求解是实现云制造资源快速共享与优化配置的关键,因此研究云制造优化配置对云制造的实施具有重要意义。
近年来学者对云制造资源优化配置进行了大量的研究:文献[4-5]考虑云制造服务过程中的时间和成本问题,建立云服务的组合优选模型,并分别提出利用粒子群算法、遗传算法对模型进行求解;文献[6-8]提出在云制造资源配置优化过程中基于云制造的Qos构建资源优化配置模型,并分别采用改进的粒子群算法或其他算法对模型进行求解;文献[9-10]在Qos的基础上,引入可维修度和信誉等目标约束,建立多目标优化模型,并分别提出使用灰色关联度和混沌算法对模型进行求解。这些研究大多从时间、成本和质量角度出发构建制造资源优化配置的数学模型,没有考虑云环境下制造资源具有动态性、异构性和不稳定的特点,在云服务实施过程中可能出现制造任务变化和成员服务退出、故障等问题,这些不确定因素会影响云服务的执行[11]。因此在考虑云服务质量的同时,也必须提高云服务过程中服务组合柔性,保证云服务正常的进行。
在考虑云制造资源优化配置过程中制造任务和制造资源动态变化可能影响制造资源优化组合和执行的不确定因素,在原有服务质量评价指标基础上,引入服务组合柔性指标,构建以服务质量为上层规划与服务组合柔性为下层规划的双层规划配置优化模型,并采用改进的多目标遗传算法对模型进行求解。
1 云环境下的优化配置问题
云环境下的资源配置服务主要由制造资源提供方、制造资源需求方以及服务平台三方面组成。云环境下的制造资源优化配置是指云制造服务平台依据制造服务需求方提出的制造任务,为其配置出最为合理的制造资源组合,最后由制造资源提供方完成制造任务,制造资源优化配置过程如图1所示。而资源需求者只关注任务本身,即制造资源能否顺利的完成制造任务以及制造资源是否为合适的制造资源组合,即从质量、完成时间和成本等方面进行约束;而制造资源提供者只关心能否按照制造要求完成制造任务;而服务平台则需协调制造资源需求方和制造资源提供方,保证服务的正常运行。

图1 云制造环境的制造资源
在实际的制造资源配置组合过程中,制造任务和制造服务资源具有动态变化的特点,容易出现如下的两个问题:①制造资源需求方的制造任务随着生产的推进需要对原先的制造任务进行修改、变更以及完善;②在制造资源配置后,制造资源组合可能会出现成员故障、成员退出等问题。图2反映了上述存在的两个问题,其中带有灰色阴影的图框表示制造任务或制造资源发生变化,而白色部分则表示没有发生变化。在带有灰色阴影的图框中,Ms2表示制造任务Ms中的第2个子制造任务Ms2发生了变化,而MR11、MRt1和MRtr表示在配置完成后,这些制造资源发生故障或退出而无法完成制造任务的情况。这些不确定因素会影响云服务的执行和完成,还极大的损害平台和企业的利益[12]。
因此制造资源配置过程中,在满足服务质量的基础上,还需要考虑制造资源服务组合的柔性,降低不确定因素造成的损失。

图2 制造资源配置优化过程中的不确定因素
2 制造资源配置组合的评价指标
制造资源配置组合评价指标是指服务平台为制造任务配置出符合要求的最佳制造资源或组合时所采用的多目标约束条件和评价指标。云环境下的优化配置不仅要考虑服务质量,还要考虑制造任务和制造资源变化的不确定因素。为了精确的对制造资源服务组合进行评价,构建如图3所示的组合评价指标,将制造资源配置组合评价指标分为两个服务质量指标和服务组合柔性两个部分,其中服务质量指标分为时间T、成本M、质量Q三个部分,服务组合柔性指标则包括制造任务变更的应对能力FS和制造资源变更的应对能力FT两部分。

图3 云制造配置组合评价指标
2.1 服务质量指标
制造资源服务质量指标包括时间、成本、质量、稳定性等因素,而在实际的制造资源优化配置过程中,制造资源需求方只关心提供的制造资源组合能否按照设定的要求完成制造任务,因此只选取成本、时间和质量这三个关键指标作为服务质量指标,对制造资源的配置组合进行评价,服务质量指标模型如公式(1)所示:
Qos={C,T,Q}
(1)
时间指标T:云服务组合的时间主要包括执行加工制造任务的时间。
成本M:云服务组合的成本主要包括资源提供者提供资源制造服务的成本。
质量Q:不同的制造资源组合具有不同的服务质量,并会对生产制造产生不同的影响,Q用来衡量制造资源组合的服务质量。
2.2 服务组合柔性指标
服务组合柔性是指在云服务生命周期中,众多不确定因素可能影响云制造资源的动态组合和执行时,云制造组合仍然可以完成执行制造任务的能力。这些不确定因素包括:①随着企业生产进度的进行,制造任务可能发生变化或者需要进行修改;②优化配置后,制造资源组合中成员服务可能出现退出和故障等状况。这些不确定因素容易导致无法高效的完成制造任务,极大的损害了各方的利益。因此服务组合柔性指标是反映上述不确定后,抵抗风险发生的能力。该指标由应对制造任务变化的能力和应对制造资源变化的能力组成:
(1)应对制造任务变化的能力FS
FS反映在配置优化后,当制造任务发生变更时,制造资源组合仍然可以完成制造任务的能力,FS主要受制造资源功能的多样性、制造资源的种类和合作的企业数量等影响。
(2)应对制造资源变化的能力FT
FT反映优化配置后,制造资源组合中成员发生退出和故障后,制造资源组合仍然可以完成制造任务的能力。
3 双层规划优化配置数学模型
双层规划模型是一种如式(2)、式(3)所示的具有双层递阶结构的优化模型[13],数学模型中上下层优化问题各自具有优化函数和约束条件,上层优化问题率先做出决策,决策结果对下层优化问题产生约束,而下层优化问题将自身的决策结果反馈至上层优化问题。

(2)
其中,y=y(x),由下层规划优化问题求得:

(3)
上述提出的制造资源优化配置过程需要考虑服务质量与服务组合柔性两个评级指标,即在满足服务质量的前提下,寻求最高服务组合柔性的制造资源组合,因此两个评价指标在决策评价时相对独立,但指标评价在决策评价过程又相互依存。服务质量指标的决策结果对服务组合柔性指标决策产生约束作用,而服务组合柔性的决策结果能对服务质量指标的决策进行反馈。因此提出建立针对云制造资源优化配置的双层规划数学模型,在上、下层模型中分别对服务质量指标和服务柔性指标建立数学模型与约束条件。
3.1 上层规划数学模型
(1)最小时间函数minT:
(4)

(2)最小成本函数minC:
(5)

(3)最低质量要求函数minQ:
(6)
式中,Qi为制造资源服务质量评分,而Q为制造资源组合服务质量评分均值。
在实际过程中,不同的制造资源需求者对成本、质量及时间存在着不同的偏好,因此结合制造服务需求者的偏好,采用线性加权的方法将关于服务质量的多目标优化转化为单目标优化问题,如公式(7)所示:
(7)
服务质量约束条件:
(1)时间约束
云制造资源组合在完成整个制造任务各个环节的总时间T不得超过制造资源需求方所规定的最晚任务完成期限Tmax,即:
T≤Tmax
(8)
(2)成本约束
在能完成制造任务的前提下,所有的制造资源服务组合的费用支出C不得高于制造资源需求方的最高预算制造支出Cmax,即:
C≤Cmax
(9)
(3)质量约束
在制造资源服务过程中,资源的配置组合中任意的制造资源配置组合的服务质量Q都不能低于制造资源需求方对制造服务的最低要求Qmin,即:
Q≥Qmin
(10)
3.2 下层规划数学模型
制造资源配置的服务组合柔性由应对制造任务变化的能力FS和应对制造资源变化的能力FT。
应变制造任务变化能力FS为历史制造任务稳定性评分,历史稳定性评分越高,则代表制造任务发布后,制造任务发生变化的几率越小;而应对制造资源变化的能力FT由制造服务的稳定性评分FT1与制造能力FT2两部分组成:
FT=FT1+FT2
(11)
式中,FT1指制造资源服务的稳定性,其值越大,则代表能提供的制造服务越稳定,FT2反映制造资源的制造能力,能力越大,则可认为该制造资源在制造任务变化时的应变能力越强。
实际生产中,不同的企业生产任务的稳定性有所差异,而不同的制造资源提供者应对资源变化的能力也不同,寻优的过程实际为寻求应对制造任务变化和制造资源变化综合解决能力最强的资源配置组合,因此结合对制造资源需求方和提供方的评估,将多目标优化转化为单目标优化问题,即:
maxU=ωS·FS+ωT·FT
(12)
服务组合柔性约束条件:
FS(i)≥FSmin
(13)
FT(i)≥FTmin
(14)
4 双层规划模型的算法求解
非支配排序遗传算法(NSGA)是一种基于Pareto最优的多目标优化算法,该算法是在遗传算法基础上,对个体按照支配和非支配关系进行分层并进行选择操作,通过使得优秀的个体有更大机会遗传到下一代[14]。双层规划的求解问题属于NP-Hard问题,求解过程较为困难,而NSGA-II是一种基于NSGA改进的多目标优化算法,与NSGA相比,其改进包括:①提出通过快速非支配排序,降低了计算的复杂度;②引进精英策略,通过父代与子代合并,从双倍种群中选取下一代种群,保证优良的种群个体在进化中不会丢失;③采用拥挤度比较算子,克服人为指定共享参数的缺陷,并将Pareto域中的个体能均匀扩展到整个Pareto域[15]。因此选用NSGA-II算法对模型进行求解,具体求解过程如下:
步骤1:将该算法的检索空间限制到双层规划模型的约束条件之中进行,将候选的制造资源配置组合编码处理。若制造资源的配置优化组合序列为MR13→MR22→MR32→MR41→MR54,则该配置组合对应的十进制编码为(3,2,2,1,4)。
步骤2:随机生成初始种群Pi,设初始种群数为N,对种群Pi进行快速非支配排序,然后分层计算初始种群Pi中每个个体的拥挤度。
步骤3:通过二元锦标赛选择个体进行交叉与变异,产生与初始种群数量相同的新子代种群Pq。
步骤4:合并初始种群Pi与新生成的子代种群Pi,得到一个数量为2N的组合种群Pg。
步骤5:对组合种群Pg进行快速非支配排序,分层计算所有个体的拥挤度,依据精英保留策略保留最优的N个个体,形成新的子代种群Pi+1。
步骤6:令i=i+1,继续执行步骤3~5,直到执行到最大遗传代数时停止。求解得上层规划模型目标函数的Pareto解集。
步骤7:将上次规划模型目标函数的Pareto解集代入下层模型目标函数中,分别求解目标函数值,取最优值即为双层规划模型的最终解。
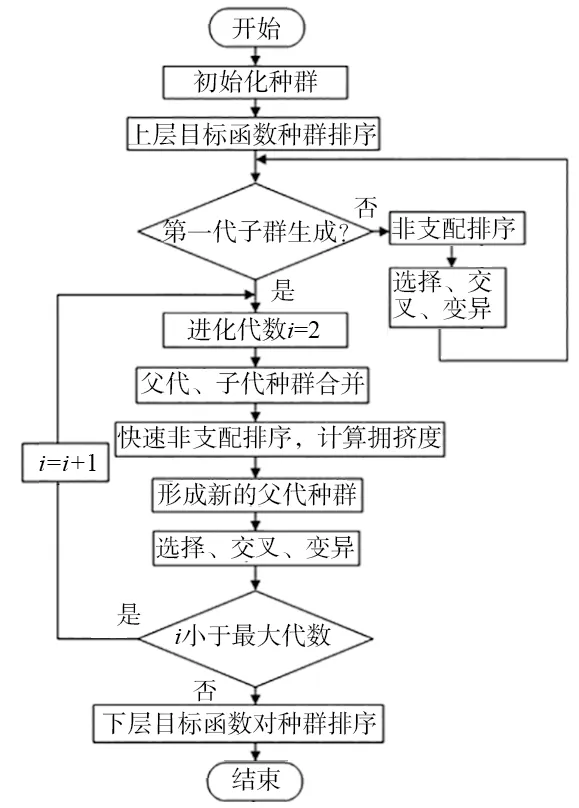
图4 基于NSGA-II的双层规划算法流程
5 算例论证
5.1 双层规划数学模型算例
某企业发布了一项制造任务,该任务可分解为4个子任务,制造服务平台对每一项子任务Msi分别进行制造资源MRij的优化配置,对应子加工制造任务的候选制造资源集如表1所示。制造资源需求方对制造任务的设定如下:最大配置优化组合时间不超过30小时、最大成本不超过1000元、最低制造要求不低于0.9;结合实际生产情况,制造成本和时间存在着底限,因此设定最小配置优化组合时间不小于20,最小成本不小于800,否则认为该配置组合不合格,而候选的制造资源服务的时间、成本等相关参数如表2所示。
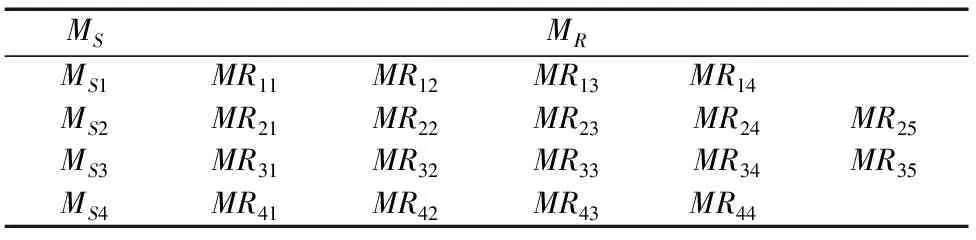
表1 候选制造资源集

表2 候选制造资源制造服务信息
在该项制造任务中,制造资源需求方的制造要求设定如下:20≤T≤30、800≤C≤1000与1≥Q≥0.9。制造资源需求方对制造时间和制造要求较高,因此设定权重分别为:ωT=0.3、ωC=0.25、ωQ=0.45。而平台服务方对组合柔性要求如下:FS≥0.88、FT≥0.92,平台方对制造服务提供方的柔性要求更高,因此设定权重分别为:ωS=0.4、ωT=0.6。则制造资源优化配置的双层规划模型如下所示:
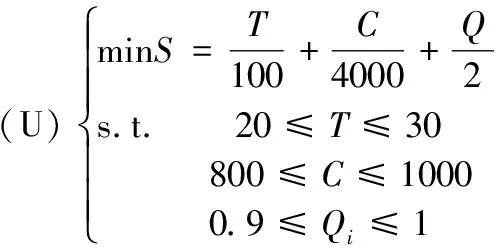
(15)

(16)
5.2 算例求解
采用NSGA-II算法对案例的双层规划数学模型进行求解,对参数的设定如下:群体规模N=50,交叉概率Pα=0.6,变异概率Pβ=0.03,最大遗传代数Gmax=50,通过Matlab 2016A计算上层规划模型的种群的适应度,种群适应度变化趋势结果如图5所示,而Pareto最优解前沿如图6所示。
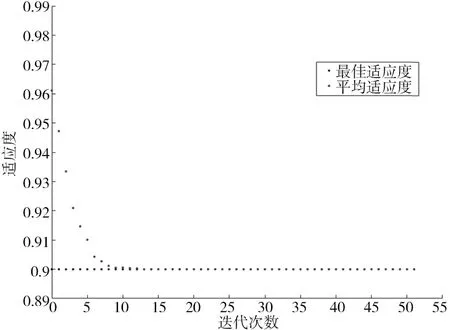
图5 种群适应度变化趋势示意图

图6 上层规划模型的Pareto前沿
将上层优化目标Pareto最优解作为可行解代入下层规划模型中,求得双层规划全局前4组最优解分别为:(MR11,MR22,MR34,MR43)、(MR11,MR22,MR31,MR43)、(MR11,MR21,MR34,MR43)和(MR11,MR21,MR31,MR43),按照全局最优进行排序,即选用(MR11,MR22,MR34,MR43)为最优的制造资源优化配置组合。
5.3 算例结果分析
本文构建的双层规划模型是将服务质量作为上层规划的优化结果来求解下层服务组合柔性规划的结果。而普通的云制造资源优化配置方法不考虑制造资源的组合柔性,即只考虑云服务过程服务质量中的时间、成本和质量三个因素。因此普通的云制造资源优化配置方法可以认为是上述双层规划模型中的上层规划。为了证明双层规划优化配置方法的有效性,采用上层规划作为普通的优化配置数学模型,并采用枚举法计算以服务质量为评价指标的优化配置方法,一共存在72组满足要求的配置组合结果,按次序列出最优的十组数据,结果如表3所示。

表3 服务质量为指标的制造资源组合最优解排序
结果表明,若以服务质量作为评价目标,则MR11→MR21→MR33→MR43为最优的制造资源组合。但从服务组合柔性角度出发,在该制造资源组合中,MR33的FS和FT值均不高,导致该组合的服务组合柔性值过低,即在实际云服务过程中,该制造资源组合很可能因为不确定因素而无法真正完成制造任务,因此从降低优化配置风险的角度来看,该组合不可取。而双层规划模型求得的4组最优解,按次序排列分别位于第4、8、2和6位,这4组解在具有较高的服务质量的同时,具有很高的服务组合柔性,即制造资源组合在实施过程中受不确定因素导致制造任务无法完成的风险较小。因此上述关于面向云制造资源优化配置的双层规划模型具有可行性。
6 结论
在分析云制造资源配置优化过程中只考虑服务质量指标的基础上,充分考虑制造任务变化和制造资源变化导致的不确定因素,建立包括服务质量与服务组合柔性的组合评价体系,提高了优化配置评价的准确性。构建面向云制造资源优化配置的双层规划数学模型,并采用改进的多目标遗传算法对模型进行求解,最后用算例验证了该方法的可行性。本文主要考虑的是从串行任务结构的角度进行云制造资源的优化配置方法研究,而实际生产制造过程中任务结构包括并行、循环、选择和混合任务结构,这些复杂任务结构的制造资源优化配置方法仍需要新的理论模型和求解方法。下一步,将针对云环境下的复杂制造任务的制造资源优化配置方法进行研究。
