仓储物流中自动导引车的路径规划研究*
2019-01-03刘敬一孙维堂董君陶
刘敬一,孙维堂,刘 闽,董君陶
(1.中国科学院大学,北京 100049;2.中国科学院 沈阳计算技术研究所 智能控制与装备部,沈阳 110168;3.沈阳市环境监测中心站 沈阳 110000;4沈阳市第二十七中学 沈阳 110011)
0 引言
随着柔性制造系统的广泛应用,国内对自动导引车的需求量也渐渐增长。在整个自动化仓储物流中,AGV运输成本占总成本比重较高,仓储任务的精准调度以及AGV良好的路径规划策略,对提高物流作业效率、降低运输成本有重要意义。
针对多AGV的路径寻优问题,刘国栋等[1]提出了一种两阶段的交通控制方法来解决AGV路径冲突问题,王佳溶[2]提出改进型的两阶段控制策略,他们针对任务的优先级未做详细描述,当任务和车辆非常多时,容易产生任务饥饿;胡彬等[3]提出一种基于时间窗的动态路径规划方法,先搜索出备选路径,然后通过计算和排布时间窗来规避冲突,但提出的时间窗是基于边的,也就是一条较长车道只能被一台AGV保留,效率比节点时间窗低。
对AGV路径规划中路径成本最优化以及调度效率问题,提出一种基于优先级队列和时间窗动态排序的路径规划方法。首先构建任务优先级队列,然后用A-Star算法启发式搜索路径,通过对节点时间窗进行精确计算和加锁,实现了多AGV的路径实时规划和动态调优,在无碰撞冲突条件下保证了仓储物流路径成本最低,而且提高了系统运行效率。
1 问题描述
1.1 环境地图
本文所考虑的是自动化仓储物流中AGV群体运动规则问题,根据其所在的仓储环境采用拓扑建模法构建地图,并作以下假设:
(1)相邻节点间的路线为单行道可双向行驶。
(2)AGV在4个方向上以同一速度匀速行驶,且转向速度固定;
(3)AGV间安全制动距离为0.8m;
(4)AGV共有4种状态:无任务静止状态(包括充电状态),有任务待负载行驶状态,负载搬运状态,临时等待状态。

图1 仓储环境下拓扑地图
1.2 目标函数
针对AGV仓储物流环境,建立拓扑地图,如图1所示,在有向连接网络G=
ey={vp→vq:vp,vq∈V}
(1)
多AGV路径规划的目的是规划出一条时间代价最小的路径。AGV在仓储环境中的耗时分为到达装载点时间,搬运状态时间和避障等待时间,分别设为的tk、carrytk和Ωk。因此所有AGV的时间代价之和可由以下公式得到:
(2)
其中,k为仓储任务的编号。
1.3 任务调度
(1)亟待充电且携带任务,将已分配的任务作为高优先级重新分配,然后将充电任务作为中优先级重新分配;
(2)亟待充电且无任务无负载,将充电任务作为中优先级重新分配;
(3)一般性实时任务作为低优先级分配;
(4)同一优先级按照FCFS方法分配。
1.4 避障要素
(1)相向相遇冲突。如图2所示,相向行驶的两辆车相遇;

图2 相向冲突示意图
(2)垂直相遇冲突。如图3所示,垂直方向的两辆车在节点相遇;
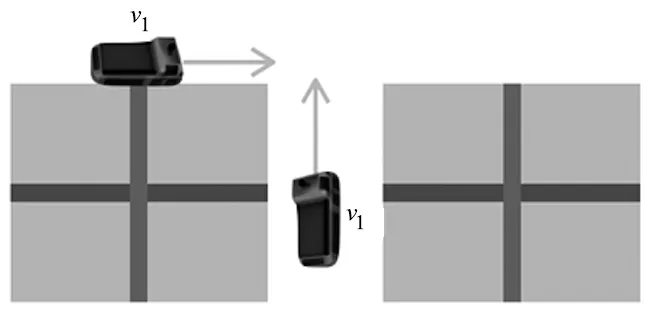
图3 垂直相遇冲突示意图
(3)占位冲突(车辆空闲)。如图4所示,前方因AGV空闲停车阻止了其他车的前进。
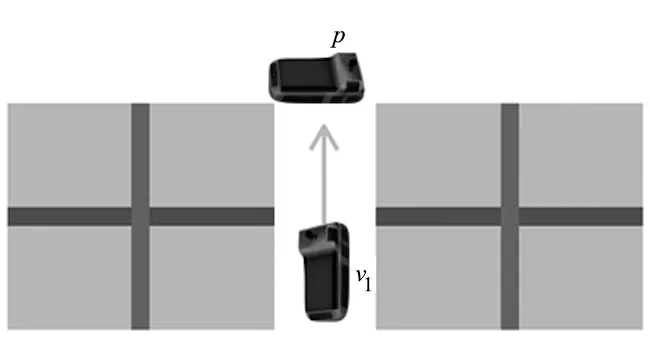
图4 占位冲突1示意图
(4)占位冲突(故障)。如图5所示,前方因故障停车阻止了其他车的前进。
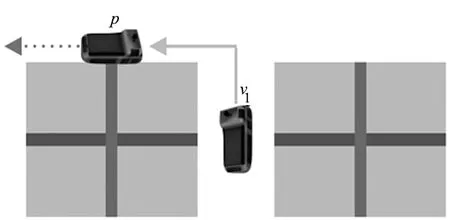
图5 占位冲突2示意图
(5)追尾冲突(超速)。如图6所示,即将赶超。

图6 追尾冲突示意图
2 基于时间窗的避障路线规划法
2.1 时间窗定义
如图1所示,在有向连接网络G=(V,E)中,假设有x辆车参与任务执行,那么任务的AGV集合为A={a1,a2,…,ax}。所有任务的起点、终点都不同,那么任务的起点集合和终点的集合分别记为S和D,且S⊆V,D⊆V。那么自动导引车所经过节点的时间窗可以定义为:
(3)

图7 节点保留时间窗模型图
2.2 时间窗计算
为了保障仓储物流过程的安全性,需要对时间窗进行精准计算,如图7所示。设AGV到达节点i的时间为ti,则有公式:
(4)
其中,tb为车辆安全制动时间,te为允许最大误差时间,包括在节点处突发断电及故障引起的制动误差。
如图8所示,设AGV车身的长度为l,AGV直行通过节点时,则有公式:
(5)
其中,vst是小车统一默认的直行速度。

图8 自动导引车通过节点i示意图
如图9所示,当AGV在节点处转弯时,则有:
(6)
其中,vtu是小车转弯通过节点的速度。
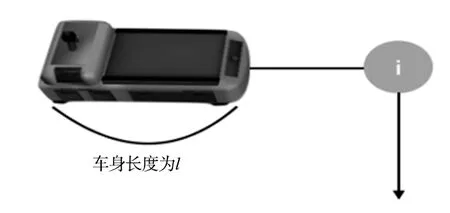
图9 自动导引车转弯通过节点i示意图
2.3 AGV最优路径规划算法
在进行多AGV路径寻优时,采用拓扑建模法构建仓储电子地图,且携带任务的AGV在运行过程中可双向行驶。将一个仓储搬运任务定义为:
carryk(t)={PQk(t),btk,Sk,Dk,LBk(t)}
(7)
其中,PQk表示第k个任务的实时优先级,参数越大优先级越低;btk表示第k个任务的开始时间;Sk和Dk分别表示第k个任务的装载点和卸载点,且Sk∈V、Dk∈V;枚举类型的参数LBk(t)表示第k个任务的搬运状态,如公式(8)所示。

(8)
给任务分配不同的优先级PQ:如图10所示,将任务队列划分为高中低三个优先级队列,分别用PQh、PQm和PQl来表示。
(1)当LBk(t)=0时,小车正在去装载点的路途中,即当有任务无负载的AGV小车亟待充电或突发断电等故障时,已安排的任务的需要重新分配,将该任务carryk(t)放入高优先级队列,将充电或维修任务放入中优先级队列;
(2)当LBk(t)=1时,AGV在装载点Sk和目的地Dk之间,即有任务有负载的AGV亟待充电或突发断电等故障时,已安排的任务的需要重新初始化,因为装载点Sk已经改变,然后将新任务carryk(t)放入高优先级队列,将充电或维修任务放入中优先级队列;
(3) 把一般性实时任务放入低优先级队列。
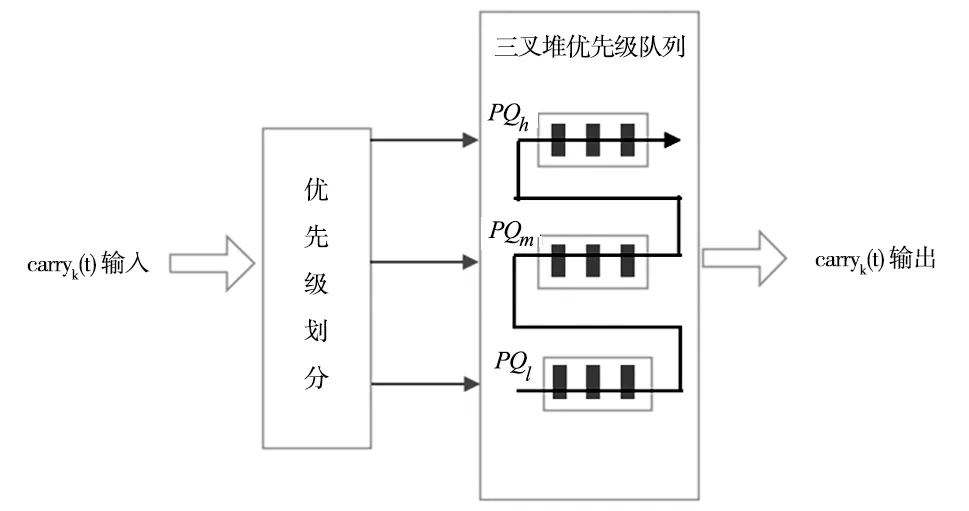
图10 三叉堆优先级队列示意图

体现在冲突一:后续的长任务需要不断地寻找次优路线;体现在冲突二:后续的长任务需要不断地负载等待。二者都容易造成任务饥饿,会降低调度系统的效率。
我们有了任务的优先级分配和时间窗的计算,下面来介绍路径规划算法的具体实现步骤,如图11所示。
(1)根据上位机系统管理员输入仓储物流参数,将任务划分优先级,插入优先级队列,并初始化多个运输任务,carryk(t)={PQk(t),btk,Sk,Dk,LBk(t)}。
(2)按照任务的优先级顺序进行车辆调度:选用离装载点[6]最近的空闲AGV来执行任务。
(3)用A-Star算法对路径进行启发式搜索,得到临时的最短行驶路径。

(5)初始化节点时间窗Wk,如果存在任务p和q使Wp∩Wq≠∅,说明节点时间窗因尚未加锁而出现重叠现象,即在的某个保留时间窗内出现了其他车辆[7]。
(6)根据重叠时间窗和拓扑地图,来确定将会发生哪种节点冲突,然后对每个节点的时间窗加锁。如果存在如图2所示的冲突一相向相遇冲突[8],选择PQk(t)较大的任务重新调度,由于根据启发式算法规划的临时最优路线会出现碰撞[9],因此需要继续搜索次优路径,返回执行步骤(3),若最后所有路线都会出现冲突一,那么返回执行步骤(2)更换AGV车辆;如果冲突类型只剩冲突二垂直相遇冲突[10],那么携带低优先级任务的AGV原地等待一个节点时间窗的时间,直到重叠窗口消失;如果两种冲突都存在,则先按照相向相遇冲突处理。
(7)生成可执行任务(指定AGV,明确路线),AGV执行完任务空闲后,由于该AGV可能成为其他任务的障碍,所以要优先派发该车辆。重复执行步骤(1)等待管理员动态分发新需求。

图11 AGV路径规划算法流程图
考虑其他三种冲突,任务执行过程中,对于冲突三,那么将更改此空闲AGV所占有的节点周围四条边的权重为无穷大,修改任务的起始点,执行算法中的步骤(3);对于冲突四,可能为突发断电(非亟待充电提醒)或机械老化等故障,需要人工维修或清除,然后更新可用AGV信息;对于冲突五,由于环境中假设AGV速度相同,所以不会出现赶超冲突,即使在前面的AGV制动减速的时候也不会出现赶超冲突,因为在计算时间窗时,AGV制动时间tb已经被保留在时间窗内。
3 算法仿真验证
使用 Visual Studio 2015作为仿真开发平台,编写调度程序对提出的路径寻优算法进行验证。选取某仓储物流中心如图1拓扑地图所示,仓储区域长30m,宽30m,仓储节点36(不包括充电区域),144个货架,14条车道纵横交错,AGV直行速度为0.5m/s。转向时间固定为2s。
设计两组仿真对比实验:一组是无时间窗加锁和有时间窗加锁的路径寻优结果,另一组是不含优先级队列和含优先级队列的路径寻优结果。从两个维度来验证所提出算法的可行性和高效性。
(1)针对第一种仿真对比实验,我们分别初始化三个任务:
carry1(t)={1,0,a1,c5, -1}。
carry2(t)={2,0,g3,b3, -1}。
carry3(t)={3,0,e1,b2, -1}。
首先根据任务的预估时间来初始化优先级,时间越长,PQk(t)数字越小,优先级越高。
无时间窗加锁的情况如图12所示,执行任务carry1(t)的车辆将会与执行carry3(t)的车辆在b1到c1路段发生相向相遇冲突,执行任务carry1(t)的车辆将会与执行carry2(t)的车辆在c3节点发生垂直相遇冲突[11];

图12 无时间窗加锁含优先级路径寻优结果
含时间窗加锁的情况如图13所示,由于经过时间窗的重新排布,任务carry3(t)已经重新规划路线,有效避免与任务carry1(t)相向相遇冲突,且在节点c2进行等待规避,避免垂直相遇冲突,任务carry3(t)将会在节点c3处进行规避等待,有效避免死锁和碰撞[12]。

图13 含时间窗加锁含优先级路径寻优结果
(2)针对第二种仿真对比实验,在不含优先级的算法中我们分别初始化三个任务,这里PQk(t)均为1,即:
carry1(t)={1,0,a1,c5, -1}。
carry2(t)={1,0,g3,b3, -1}。
carry3(t)={1,0,e1,b2, -1}。
算法执行过程如图14所示。

图14 含时间窗加锁不含优先级路径寻优结果
考虑图13和图14所示的两种仿真执行过程,对不含优先级和含优先级的两种调度算法进行路径代价对比,如表1和表2所示。根据目标函数公式计算出:含优先级的调度算法路径成本Cost小于不含优先级的调度算法。

表1 不含优先级队列的调度算法执行分析
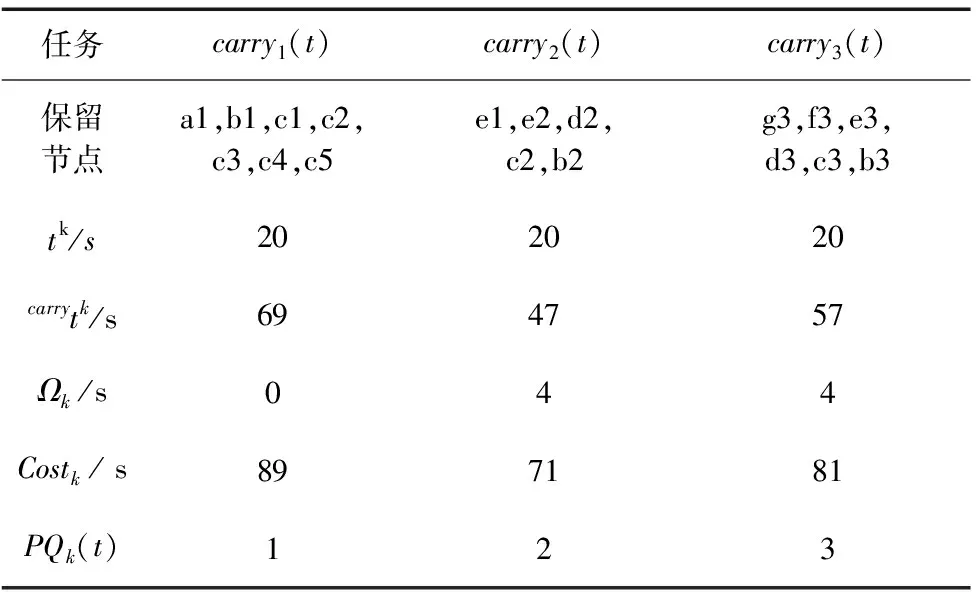
表2 含优先级队列的调度算法执行分析
4 结论
对多AGV路径寻优和调度效率问题,提出基于优先级队列和时间窗模型的调度算法。在多AGV动态路径寻优中,解决了多AGV的碰撞冲突问题,而且通过构建任务优先级队列优先级优化了调度顺序,不仅保证了路径最优,而且可以避免任务饥饿与死锁。最后通过仿真实验得出,算法在保证车辆无碰撞的条件下可使AGV路径成本最低,同时提高了任务和车辆调度的效率。
