基于时间延迟的飞机结构维修优化研究*

2019-01-03余芬，阮峰，张鑫

组合机床与自动化加工技术 2018年12期

余芬，阮峰，张鑫

(中国民航大学航空工程学院，天津 300300)

0 引言

飞机结构维修是维修大纲的重要组成部分。在保证飞机安全适航的前提下，有效减少飞机结构维修费用具有十分重要的意义。可用度是飞机结构重要的功能保障指标，维修费用率是维修工作中重要的经济性指标，这两者都与飞机结构故障检测间隔大小有关，检测间隔过大，将会使结构可用度降低，检测间隔过小，将会使维修费用率增大。

对于飞机结构的故障检测间隔和维修优化，近年来国内外学者都做了大量的研究。Rajiv N Rai等以军用航空可修系统的主要失效模式为对象，提出了一种基于可用度的维修优化模型[1]。C D van Oosterom等基于系统的时间延迟特性提出了延迟更换这一维修措施，从而降低维修成本[2]。Wenbin Wang扩展了时间延迟概念，提出了基于三阶段故障过程的检测模型[3]。Li Yang等基于时间延迟特性针对单部件系统提出了定期和随机相结合的检测策略[4]。蔡景等考虑了故障检测的不完备性，提出了不等间隔检测检测策略[5]，研究了基于有限时间的不完备检测[6]。吕德峰等考虑了结构的不完美维修，建立了基于可用度的故障检测优化模型[7]。陆晓华等针对飞机发动机系统维修提出了一种多目标优化模型[8]。文献[1，7]在建模时引入了役龄回退因子，考虑了维修的不完美性，文献[2]根据所建立的模型给出了延迟更换下的最优检测策略，文献[4]针对两种不同的检测策略提出不同的维修方式，并建立了维修优化模型，但是都将故障检测定义为完备的。文献[3] 考虑了故障检测的不完备性，并将结构工作时的功能状态细分成三个阶段，文献[8]对缺陷延迟时间和维修费用率进行多目标优化，但是都将故障检出概率视为一个定值，与实际不符。文献[5-6]考虑了故障检测的不完备性，并且故障检出概率是随着时间变化的值，但是仅考虑维修费用率的最小化，优化目标过于单一。

本文针对飞机结构维修故障检测的不完备性，考虑了故障检出概率的具体分布，以可用度为约束，以维修费用率为目标，提出了基于时间延迟的飞机结构维修优化模型，通过仿真计算，给出了不同条件下模型的最优解，为实际的维修决策优化提供参考。

1 飞机结构故障检测策略

根据飞机结构损伤容限设计特点，其故障都具有时间延迟性。结构一般首先发生潜在故障，而后再经过一段时间发生功能故障的特性叫做时间延迟[9]。由潜在故障点到功能故障点的这段时间为延迟时间。在延迟时间内结构依然能够维持正常的功能。具有时间延迟特性的结构状态通常可以分为三种：正常状态S1，潜在故障状态S2，功能故障状态S3[10]。飞机结构的故障延迟示意图如图1所示，μ为潜在故障产生时间，τ为延迟时间。

图1 故障延迟示意图

根据MSG-3结构维修要求可知，飞机结构主要采取定期检测的视情维修策略，因此采用首次检测和重复检测的不等间隔检测策略。

(1)结构工作到首次检测间隔kT时进行第一次检测(k为首检期系数，T为重复检测间隔，其中k取正整数)，以后每隔周期T进行一次重复检测；

(2)检测发现结构功能正常，则不进行维修；

(3)检测发现潜在故障，就及时进行预防性维修，以避免潜在故障进一步扩展；

(4)检测发现功能故障，说明结构处于失效状态，立即进行修复性维修。

2 飞机结构维修优化模型

2.1 模型假设

为了便于维修优化模型的建立，作出如下假设：

(1)潜在故障检测是不完备的，由维修大纲知，可以采用三种不同的检测等级。根据研究，潜在故障检出概率服从威布尔分布，其在例行检测时被检测到的概率为：

(1)

(2)结构出现功能故障后就会失效，在检测时一定会发现；

(3)结构的检测和维修工作所占用的时间相对于结构整个寿命周期来说可以忽略不计；

(4)预防性维修和修复性维修可以使结构恢复如新。

2.2 可用度模型

可用度是指结构在某时刻具有或维持其规定功能的概率，可表示为结构可工作时间与预期的寿命周期(可工作时间与不可工作时间之和)之比[12]。

假定飞机结构的潜在故障出现的时间μ的概率密度函数和累积分布函数分别为f(μ)和F(μ)，延迟时间τ的概率密度函数和累积分布函数分别为g(τ)和G(τ)，其中μ和τ相互独立。

定义结构从开始工作到检测到潜在故障或发生功能故障为一个寿命周期。

由于故障检测采用不等间隔检测策略，将检测分为(0,kT)和[(k+n)T,(k+n+1)T]两个阶段，n≥0。

(1)在(0,kT)内潜在故障产生并扩展到功能故障概率为：

(2)

(2)在(0,kT)内潜在故障产生却并未扩展，在kT时刻检测时发现该潜在故障的概率为：

(3)

由式(2)、式(3)得，在(0,kT)内结构可工作的时间为：

(4)

预期寿命周期为：

(5)

(3)在[(k+n)T,(k+n+1)T]内潜在故障扩展到功能故障

潜在故障在[(k+n-m)T,(k+n-m+1)T]内产生，在后来的m次检测中却被连续漏检，最终导致在[(k+n)T,(k+n+1)T]期间内扩展到功能故障的概率为：

(6)

当n-m=-1时，(k+n-m)T取0，表示潜在故障在(0,kT)内产生，以下同理。

(4)在(k+n+1)T时检测到功能故障

潜在故障在[(k+n-m)T,(k+n-m+1)T]内产生，在后来的m次检测中被连续漏检，却没有扩展到功能故障，最后在(k+n+1)T时刻检测到潜在故障的概率为：

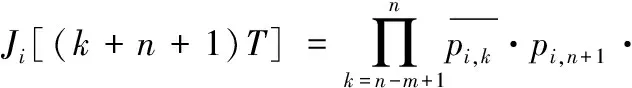
(7)

由式(6)、式(7)得，结构可工作时间为：

(8)

预期的寿命周期为：

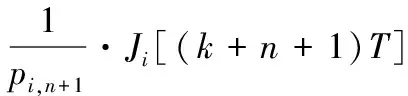
(9)

综合以上分析，由式(4)、式(8)知，结构在一个寿命周期内可工作时间为：

遗传因素对于肉牛的饲料利用率有非常大的影响，因为不同肉牛品种之间存在有很大的遗传差异性，其遗传性状也不尽相同，直接影响了肉牛的饲料利用率。通常肉牛品种还具有生长发育速度快、成熟早、增重快以及饲料利用率高的特点。但是我国目前采用的肉牛品种大多是黄牛，但是黄牛的先天遗传性状也决定其具有生长速度慢、饲料利用率低以及产肉能力过差的问题，在养殖中还需要耗费大量的饲料。通过将一些品种优良的肉牛品种与黄牛进行杂交，其后代还能拥有生长速度快、牛肉品质好的饲养优势，使饲料利用率得到进一步提升[1]。

(10)

由式(5)、式(9)知，预期的寿命周期为：

(11)

根据可用度定义，由式(10)、式(11)知，结构可用度为：

(12)

2.3 维修费用率模型

设一次故障检测的费用为Ci，一次潜在故障的维修费用为Cp，一次功能故障造成的故障损失费用为Cf(包括修复性维修费用和功能故障造成的停机费用以及其他损失)。

将三种费用分开考虑如下：

由式(3)、式(6)、式(7)得，故障检测费用为：

(13)

由式(3)、式(7)得，潜在故障的维修费用为：

(14)

由式(2)、式(6)得，功能故障造成的故障损失费用为：

(15)

综合式(13)～式(15)得，一个更新周期内结构的期望维修费用为：

EC(k,T,i)=Ei(Ci)+Ei(Cp)+Ei(Cf)

(16)

(17)

2.4 飞机结构维修优化模型的建立

为了保证飞机结构的安全性，总是希望潜在故障产生后在下一个检测点就被检测到，因此，首次检测间隔应该在潜在故障出现之前，所以kT≤ΔTμ(ΔTμ为出现潜在故障的平均时间)，同时为了要求潜在故障在扩展到功能故障之前能被检测到，因此重复检测间隔必须小于平均延迟时间，所以T≤ΔTτ(ΔTτ为延迟时间的平均值)。

以首检期系数k，检测周期T和检测等级i为优化变量，以可用度为约束，以维修费用率为优化目标，建立基于时间延迟的不完备检测维修优化模型如下：

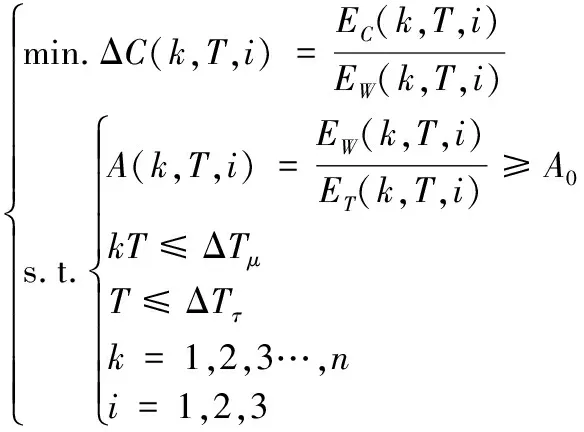
(18)

3 实例分析

以飞机主起落架支撑梁为例，根据某航空公司提供的数据，潜在故障产生的时间和延迟时间的分布函数服从威布尔分布，经过参数估计与假设检验得到其参数如表1所示[11]。

表1 威布尔分布参数

飞机主起落架支撑梁的潜在故障发生时间μ和延迟时间τ的分布函数分别为：

(19)

(20)

每次例行检测的费用Ci按照目视检测、详细检测、特殊详细检测分别为100元、200元、400元。对于三种不同的检测等级，潜在故障检出概率不同，设定α1=0.80，α2=0.75，α3=0.70；β1=0.70，β2=0.50，β3=0.35。预防性维修费用Cp为3000元，功能故障损失费用率Cf为200元/飞行小时。产生潜在故障的平均时间ΔTμ为15330飞行小时，平均延迟时间ΔTτ为1642飞行小时。

将各参数代入式(18)中，用MATLAB对优化模型进行仿真计算，得到不同检测等级下满足可用度的最小维修费用率ΔC(k,T,i)和对应的最优首检期系数k和最优重复检测间隔T。三种检测等级下对应不同可用度的最优解如下表2～表4所示。

表2 目视检测下的最优解

表3 详细检测下的最优解

表4 特殊详细检测下的最优解

由表2～表4中的计算数据可知，当可用度A0分别为0.93、0.98时，最优检测等级均为i=1，即目视检测，此时的首检期系数k和重复检测间隔T分别为k=3，T=330飞行小时和k=3，T=250飞行小时。同时注意到，在目视检测下，可用度A0为0.93时最小维修费用率要比A0为0.98时减少4.3%。

设定可用度A0=0.93，列出三种检测等级下等间隔检测(k=1)和不等间隔检测(k=3)下的最优解如表5～表7所示。

表5 目视检测下的最优解对比

表6 详细检测下的最优解对比

表7 特殊详细检测下的最优解对比

由表5～表7中的计算数据可知，三种检测等级下不等间隔检测策略下的维修费用率比等间隔检测策略下的维修费用率分别减少18.0%、17.3%、18.1%。即不管采用何种检测等级，不等间隔检测策略都比等间隔检测策略要好。

限于篇幅，只列出目视检测下不同首检期系数k的可用度变化图和维修费用率变化图。

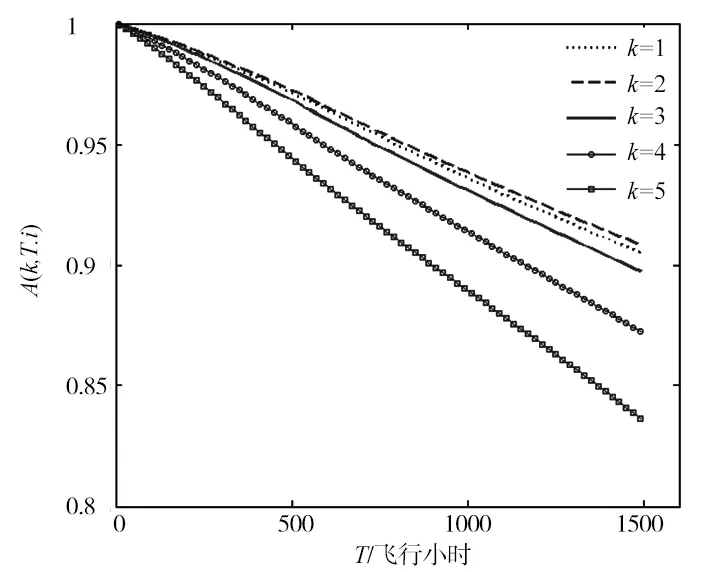
图2 不同k值对应的可用度变化图

图3 不同k值对应的维修费用率变化图

由图2、图3可知，目视检测下，随着首检期系数k的增大，结构可用度整体是不断减小的，最优重复检测间隔T的值也是逐渐减小的；同一首检期系数下，重复检测间隔T越大，可用度越小。对于详细检测和特殊详细检测来说，同样有这样的规律。

三种检测等级下的最优首检期系数(k=3)对应的可用度变化图和维修费用率变化图分别如图4、图5所示。

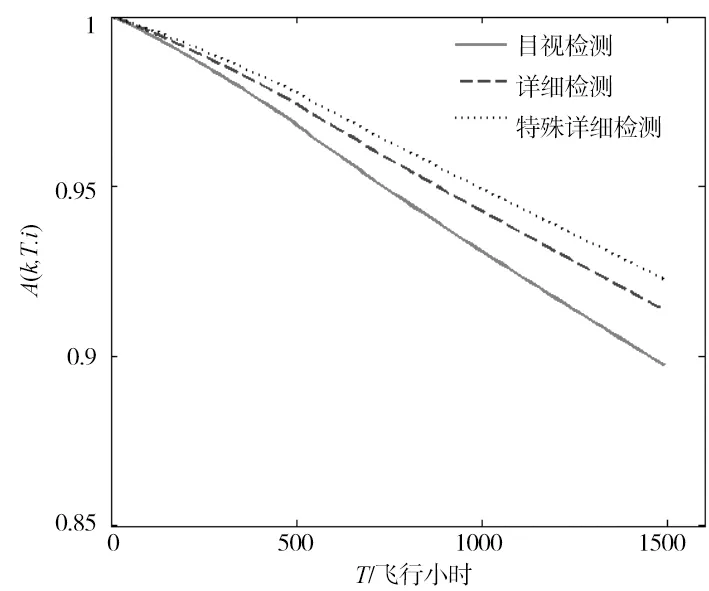
图4 k=3时三种检测等级下可用度变化图

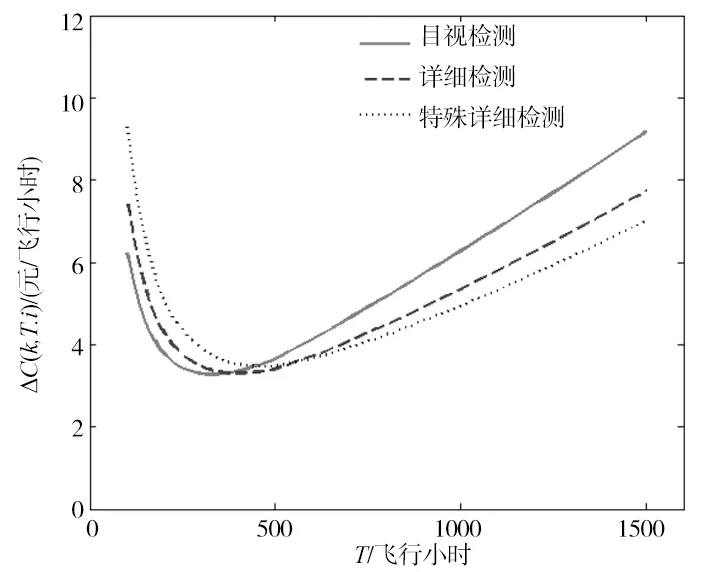
图5 k=3时三种检测等级下维修费用率变化图

由图4可以看出在目视检测、详细检测、特殊详细检测三种不同的检测等级下结构的可用度是逐级递增的，这说明在维修中提高检测等级能够及时发现潜在故障，避免功能故障的产生，提高结构可用度。由图5可知，三种检测等级中目视检测的平均维修费用率最低。在可用度A0取0.93时，最低维修费用率ΔC(k,T,i)分别为：3.2684元/飞行小时、3.2959元/飞行小时、3.4587元/飞行小时，对应的重复检测间隔T分别为：330飞行小时、380飞行小时、480飞行小时。

目视检测下，k=3时的例行故障检测费用E(Ci)、潜在故障维修费用E(Cp)、功能故障损失费用E(Cf)的变化图如图6所示。

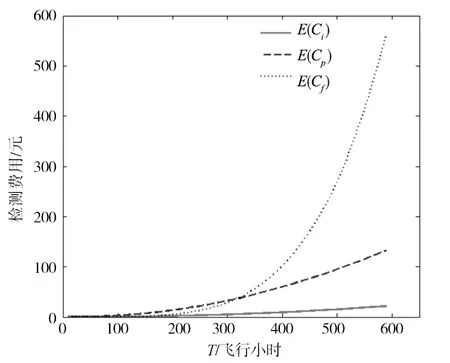
图6 目视检测下三种维修费用变化图

由图6可知，在最优重复检测间隔T值之后，随着重复检测间隔的增大，功能故障损失费用E(Cf)急剧增大，其值远远大于故障检测费用E(Ci)和潜在故障维修费用E(Cp)，由此造成高额的维修费用支出，这是由于在最优重复检测间隔T之后，由于重复检测间隔逐渐增大，结构发生功能故障的概率也就越大，由此造成的功能故障费用损失占总维修费用支出绝大部分，同时还会导致结构可用度的降低。