等基圆锥齿轮的齿面建模与加工仿真*

王 斌，孙 逊，徐爱军，李聚波

(河南科技大学 机电工程学院，河南 洛阳 471003)

0 引言

UG软件将零件加工的几何造型、刀位、图形显示和后置处理等作业过程结合在一起，可以有效地解决复杂零件的编程来源、图形显示、走刀模拟和交互修改等问题，是预防数控加工中机床、刀具、夹具相互之间的干涉碰撞问题的有效手段。

从现有资料及报道可知，借助UG软件，使用球头铣刀加工弧齿锥齿轮、直齿锥齿轮等的仿真加工比较多见，并且已经应用于实际[1-2]。但是未见基于球头铣刀的针对等基圆锥齿轮的相关技术及研究。

根据传统的等基圆锥齿轮理论，加工等基圆锥齿轮时，使用成形指状铣刀，通过控制刀具以及轮坯之间的运动，使二者之间实现特定的运动，从而使齿轮在任意锥距位置处当量齿轮的基圆半径相等，齿廓也不会发生突变[3-4]。从而实现一把铣刀精确加工整个齿面。但是由于该指状铣刀属于专用刀具，其轴截形的廓形精度保证依靠于样板的精度及工人的技术水平，刀具制造精度低，加之大型齿轮加工中由于刀具磨损，必须多次换刀，多把指状铣刀的精度一致性难以保证，导致等基圆锥齿轮加工中刀具制造难度加大，齿轮的加工精度低[5-7]。所以，如果用指状铣刀只对等基圆齿面进行粗加工及半精加工，精加工时使用通用的球头铣刀，是提高其加工精度，降低制造成本的有效途径。

为此，本文以等基圆锥齿轮理论为基础，通过齿面分析及建模，利用UG软件实现对等基圆锥齿轮的仿真数控加工，并利用VERICUT软件，基于UG生成的加工代码，进一步进行了齿面的仿真加工，在此基础上，对理论齿面和实际加工的齿面进行了分析对比。实现了利用标准球头铣刀数控加工等基圆齿面，丰富了等基圆齿面的精加工技术。

1 等基圆锥齿轮特征

针对等基圆锥齿轮而言，用数控方法控制刀具与轮坯实现特定的相对运动，加工出特殊齿线，得到不同锥距处基圆半径相同的锥齿轮—等基圆曲线齿锥齿轮，其特征为：

(1)

式中，z为锥齿轮齿数，mte为锥距Re处端面模数(mm)，αn为齿廓法面压力角(°)，δe为锥齿轮分度角(°)，βe为锥齿轮大端螺旋角(°)。

由式(1)得齿线螺旋角β与锥距R的关系为：

(2)

式中，Re为锥齿轮大端处的锥距。

2 等基圆锥齿轮齿面建模

2.1 加工坐标系的建立

图1为球头铣刀切削等基圆锥齿轮过程中，刀具与轮坯在切齿坐标系中的相对位置关系。当球头铣刀由大端向小端以一定的速度运动时，轮坯按特定规律变速回转，球头铣刀的刀心沿着实际齿线的等距线运动，即包络出等基圆锥齿轮齿面。

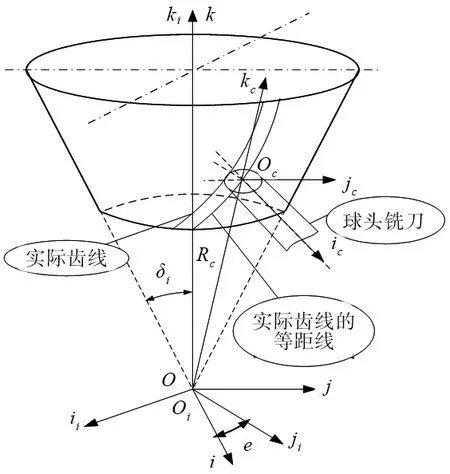
图1 等基圆锥齿轮的切齿坐标系

σi(Oi-iijiki)为固联于轮坯的坐标系，原点Oi位于锥顶，理论齿线的大端在jioiki在平面内。

σc(Oi-iijiki)为固联于刀具的坐标系，用以描述刀具轴截形绕ic轴旋转形成的刀具曲面。切齿过程中，刀具轴线始终垂直于分锥母线，刀具坐标系沿分锥母线平动，Oc位于分锥母线上。

σ(O-ijk)为空间固定坐标系，用以实现σi与σc之间的关系变换，原点O与轮坯的坐标系原点oi重合。切齿过程中，刀具轴线始终在固定坐标系的iok平面内，jc与j保持平行。

σ与σc原点间的矢量关系为：

OOc=Rc=Rc(sinδii+cosδik)

(3)

式中，Rc为刀具中心与轮坯锥顶之间的矢量，δi为被加工齿轮根锥角(i=1,2分别对应小轮，大轮)。

由分锥齿线冠轮平面内齿线的对滚关系，轮坯坐标系的轴与固定坐标系轴的夹角为：

e=θc/sinδi

(4)

式中，θc为刀具中心在锥距Ri处对应的极角。

各坐标系间的变换矩阵为：

(5)

(6)

2.2 齿面方程齿面的离散化处理

等基圆锥齿轮齿面方程的获得最初是基于指状铣刀加工理论的。在刀具坐标系内，刀具曲面和齿轮齿面之间接触点满足啮合方程，通过求解啮合方程得到等基圆锥齿轮的齿面方程：

r(i)=[MiO][MOC]r(c)+[MiO]Rc

(7)

根据上述齿面方程，代入各参数，简化处理后，得到齿面离散点的计算公式：

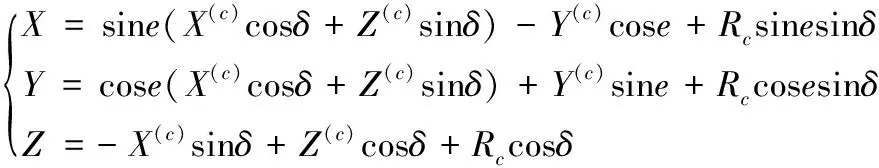
(8)

上式中：

(9)

上式中，sk为半径为rk处的齿廓修形量，rv为当量齿轮分度圆半径，Tk为直线OaK与刀具轴线的夹角，Oa为当量直齿轮中心，γ为刀具轴截形绕其轴线顺时针回转角度。

2.3 齿轮三维模型的建立

在等基圆锥齿轮的齿面方程中，通过锥距参数的一系列不同取值，结合上述离散点计算公式，就可以得到齿面离散点坐标，表1所示为算例齿轮的几何参数，具体计算后得到凹凸齿面离散点坐标，这些瞬时离散点构成齿面的接触线族，通过这一系列接触线族，构成齿轮的空间曲面。对这些离散点进行提取，导入UG中就构成了齿面片体，从而完成对齿轮的三维建模。如图2所示为精加工后的齿面片体。

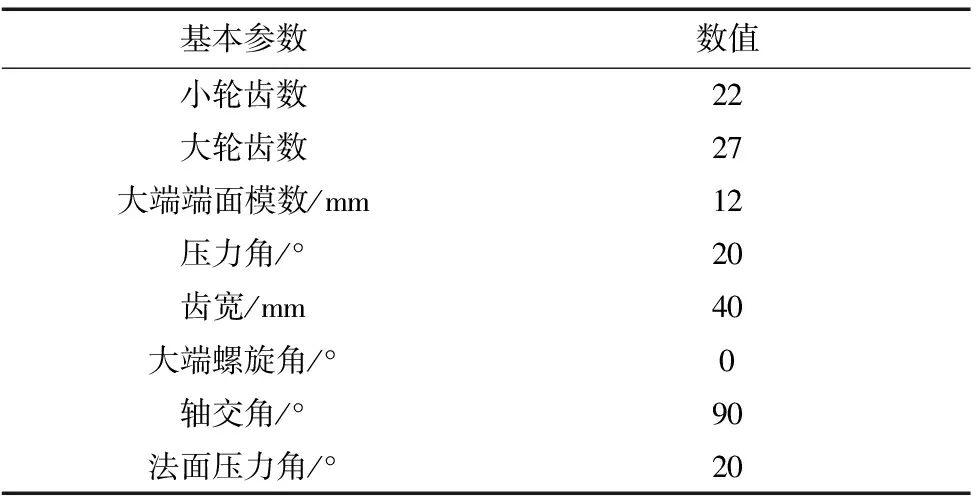
表1 齿轮副基本参数表

图2 齿面片体

而后通过齿面片体生成设计齿轮精确三维模型，如图3所示。

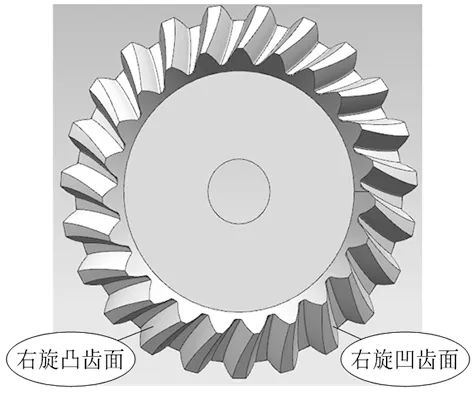
图3 等基圆锥齿轮设计三维模型

2.4 加工仿真

为了提高等基圆锥齿轮的加工效率，球头铣刀只用于最后的精加工，精加工之前的粗加工及半精加工仍采用效率较高的成形铣削。所以，为了提高仿真加工的可视性，对半精加工后的齿轮进行三维建模，将其作为齿轮毛坯，并导入UG软件，具体的仿真加工过程如下：

(1) 将齿轮的设计模型(精加工后的齿轮)和半精加工齿轮模型装配在一起，两个齿轮三维模型在装配后的原点对齐。将半精加工齿轮模型设置为需要进行加工的精加工齿轮毛坯，选取设计模型作为零件，两齿轮轮齿齿面间的距离为预设的加工余量，再导入UG软件加工环境中的齿轮上表面建立图4所示的精加工坐标系[8-10]。

图4 半精加工后齿轮(精加工齿轮毛坯)

(2) 创建精加工刀具，在刀具列表中选择球头铣刀，设置刀具参数，刀具的直径设置为6mm。

(3) 在UG加工环境中设置仿真加工齿轮的方式：选取“型腔铣”(mill-contour)作为本次加工的加工方式，子类型位置中选取“固定轴曲面轮廓铣”。

(4) 选取如图5所示轮齿的凸面为切削区域。

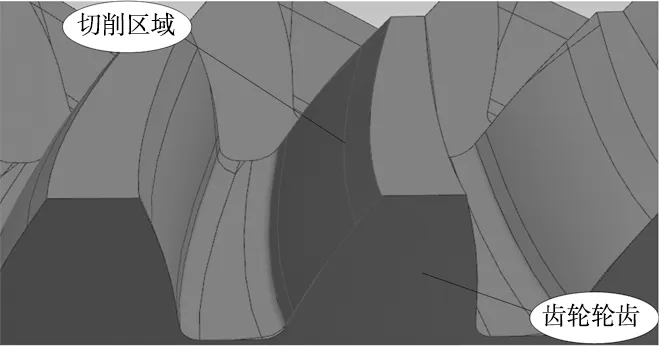
图5 切削区域

(5) 设置驱动方法为“流线驱动”，利用流线驱动方法使刀具在加工过程中的走刀路线沿着径向移动，实现对齿面的精加工过程，同时选取往复切削作为齿面精加工的切削方式[11]，将步距设置为残余高度。

(6) 点击固定轴轮廓铣对话框中的“生成”命令，生成齿轮凸面的精加工的刀具轨迹，如图6所示。

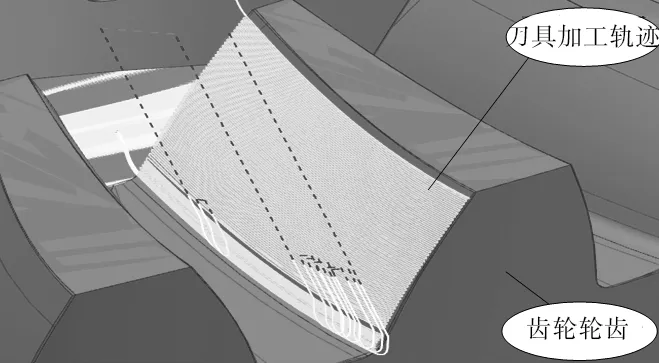
图6 刀具轨迹

(7) 加工仿真如图7和图8所示。

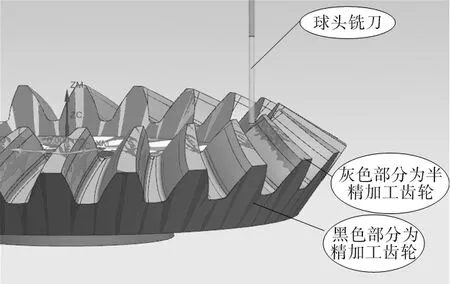
图7 UG软件加工仿真整体视图

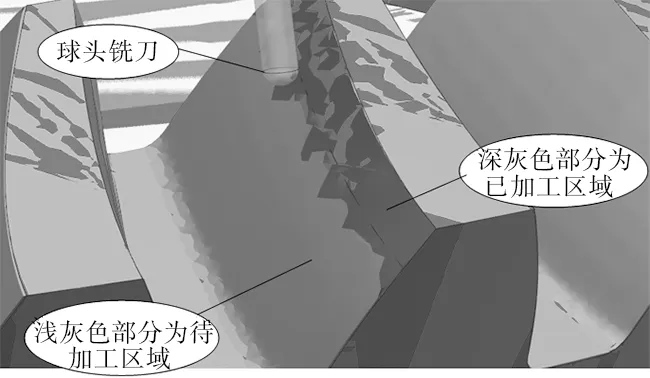
图8 UG软件加工仿真局部视图

(8) 在VERICUT软件中选取合适的机床模型，并将半精加工后的齿轮模型(待精加工件)另存为stl格式导入VERICUT软件中，并安装在机床上，整体效果如图9所示。然后导入利用UG软件生成的数控代码，对半精加工后的齿轮(工件)进行精加工[12-15]。

图9 VERICUT仿真加工图

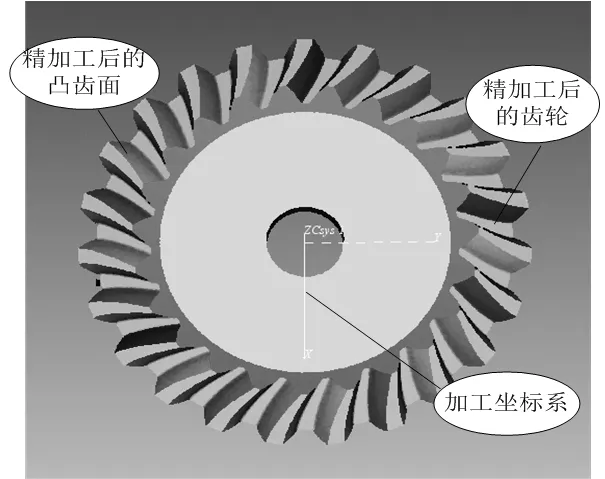
图10 VERICUT仿真加工完成的齿轮

将仿真加工所得的齿面和理论齿面进行比较分析，图10是比较分析的结果图。过切与欠切检测精度设为0.01mm，图中红色区域为过切，蓝色区域为欠切，误差小于0.01mm的显示为绿色。

由图11可知，球头铣刀加工的轮齿凹面小端有稍许过切，大端有少量欠切；加工的凸面大端有少量过切，其余部分和理论齿面重合。图11所示加工齿面与理论齿面间的少许误差，通过控制刀具步距、刀具直径大小，可加以改善。分析比较结果说明，等基圆锥齿轮的齿面建模方法、及其加工方法正确可行。

图11 加工后齿面精度分析

3 实验加工验证

将VERICUT仿真加工验证后的数控代码，导入机床，用数控机床实际加工等基圆锥齿轮来进行精加工验证。本次实验选用的机床如图12所示。将粗加工后的工件安装于夹具之上，夹具与机床的工作台连接。然后进行行对刀，并先进行试切削，试切削没有问题时，启动机床，依次完成凸凹齿面的精加工。

图12 数控雕刻机

图13为球头铣刀按照既定的路径加工齿面中。

图13 切削大轮凸面过程

由于等基圆锥齿轮的特殊性，现有齿轮检测中心没法测量其齿面，故最终加工后的齿面只能通过对滚，观察其接触区来判断切齿精度。如图14为对滚后的齿面接触情况。

图14 最终滚检效果图

可见，加工后的齿面接触区位置、形状正常，说明UG环境下齿面加工路径的规划合理，生成的齿面加工程序正确。

4 结论

根据等基圆锥齿轮理论，通过对等基圆锥齿轮的齿面建模，仿真分析及其数控加工，结果表明：

(1) 基于齿面方程、对等基圆齿面离散点的计算、提取、导入及其三维建模方法正确；

(2) 基于球头铣刀，在UG软件中对等基圆锥齿轮进行的数控加工自动编程，可以实现等基圆齿面的数控加工。