基于主成分分析的四川省城市经济发展水平评价

舒服华

经过改革开发四十年的发展，我国经济社会取得了辉煌的成就，目前已成为全球第二大经济体，不管是城市还是农村，面貌都发生了翻天覆地的变化，人民生活蒸蒸日上，不论是物质生活还是精神生活，都有了显著的改善和提高。但我国地域辽阔，人口众多，受自然条件和历史等因素影响，各地发展还很不平衡，部分地区已经步入小康社会，另有部分地区还相对贫困。党和国家对人民作出了庄严的承诺，要在2020年全面建成小康社会，这一任务既神圣又艰巨。全面建成小康社会是中华民族数千年来的期盼，全面建成小康要求我们创新发展、协调发展，统筹推进经济建设，解决好发展不平衡、不协调、不可持续的问题，使全体人民都能共享经济发展的成果。发展不平衡是由多种原因造成的，如地区的自然环境、自然资源、交通状况、劳动力状况、历史原因、思想观念、领导者水平等。欠发达地区除了靠自身的奋斗外，先发展起来的地区也应该顾全大局，帮助和带动欠发达地区加快发展，最终实现全体人民的共同富裕。

四川省是我国西部地区经济实力最强的省份，经济总量连续多年位居西部榜首。但地区发展也很不平衡，成都平原和长江沿线地区发展较快，西部少数民族聚集区发展较慢。评价地区经济发展水平，对总结地区经济发展的经验，查找不足，激励先进，鞭策落后，形成互帮互学、联手提高的良好局面，促进区域经济均衡发展等具有重要的现实意义。评价地区经济发展水平是一个系统工程，涉及的面广，涵盖的内容多，特别是所选择的评价指标，有些指标数据之间具有一定的相关性，这样，容易导致指标重复使用，影响评价的效率，增加了评价的难度。运用统计分析方法研究分析某一问题时，如果涉及的变量个数多，且变量之间有一定的相关关系，若用原始数据直接建模，就会增加研究分析的复杂性［1］。两个变量之间有很强的相关性，表明它们反映的信息有一定的重叠。主成分分析方法（PCA）［2］就是利用降维的原理，把多指标转化为少数几个综合指标，这些综合指标称为主成分，它们能够反映原始变量的大部分信息，且各自所含信息互不重复，将复杂因素归结为几个主成分，使研究的问题简单化，同时又对决策结果不会产生明显的影响，这在经济、工程领域得到了广泛的应用［3］。由于经济发展水平评价指标中，有些指标具有一定的相关性，导致指标的重叠，使评价的难度增加和效率降低［4］，为了克服这一问题，本文运用主成分分析法评价四川省部分城市经济发展水平。

一、主成分分析法简介

（一）主成分分析基本原理

主成分分析法是指将数据中具有一定相关性的指标，重新组合成一组新的不相关的综合指标来代替原来的指标，将多个相关的指标转化为少数无关指标［5］。新的指标为原指标的线性组合，对于选取的第一个新指标，用方差表示该成分的信息量，理论上而言，它的方差最大，故称为第一主成分，如果选取的第一个新指标不能完全代替原有指标的信息量，则需要选择第二个新指标，由于成分的有效性，上一个主成分的信号不会出现在第二个主成分中。以此类推，选取第三、第四个新指标，直到选择的新指标个数累积能代表原指标信息的85%以上为止［6］。

设有n个评价对象，每个评价对象有m个评价指标，xij为第i个评价对象第j个评价指标的评价值，则可构成评价矩阵 X ＝（xij）n×m，即：

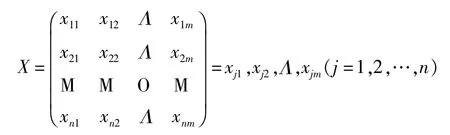
这m个线性相关的评价指标可重新组合成m个线性无关的新指标，即

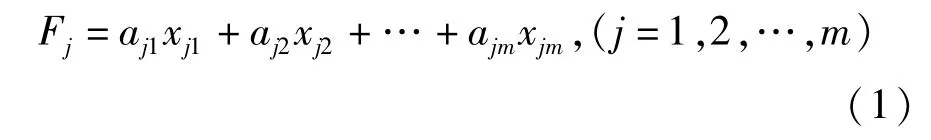
Fj称为第j个主成分，aij为载荷系数。

设λj是Fj特征值，则满足：Fi与Fj线性无关（i≠j）；λ 1＞λ2＞… ＞λm；∑ajk2＝1。

于是，主成分分析模型可表示为：

A称为主成分系数矩阵。

主成分分析方法步骤如下：

（二）主成分分析评价法步骤

1．数据标准化

式中，xij为原始数据，rij为标准化数据，μj为第 j个指标的均值，σj为第j个指标的标准差。

2．构建相关系数矩阵

计算各个指标的相关系数，根据相关系数构造相关系数矩阵。显然，相关系数矩阵为一对称矩阵。根据相关系数矩阵分析指标之间相关性。

3．计算特征值和特征向量

计算协方差矩阵的特征值和对象的特征向量，将特征值从大到小排序，特征值就是主成分的方差，其大小反映了主成分的影响力。

4．计算贡献率和累积贡献率

式中，wi为主成分 Fi贡献率，pi为F1到Fi累积贡献率，λi为Fi的特征值。

5．提取主成分

提取累积贡献率大于85%的特征值λ1、λ2、…、λt，对应的主成分为 F1、F2、…、Ft。

6．计算主成分综合得分

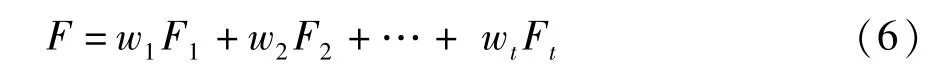
7．作出评价结果

根据综合得分判断评价对象的优劣，综合得分越高，评价对象越优［7］。

（三）主成分分析改进

传统的主成分分析没有考虑到不同的评价指标对评价对象的不同影响，将各评价指标的重要程度均等看待，这样导致了评价结果的不合理性，文中采用指标的权重加以改进，以体现不同的评价指标对评价结果的影响，使评价结果更趋合理。由于地区经济发展水平评价指标较多，文中采用较为简单的环比评分法确定评价指标的权重，这样既容易操作又可以准确表达不同指标重要性的差异。具体方法为：首先根据评价指标对评价结果的影响大小，对每个评价对象的重要程度进行评分，评分可为百分制也可为十分制，也可为小数，也可为分数，根据决策者的喜好自行决定，然后用指标得分的比重表示权重。设评价指标Xi的重要性评分为Pi，则Xi的权重为：

二、四川省城市发展水平评价

在四川省诸多城市中，成都属于副省级城市，经济发展一家独大，2017年GDP达1.4万亿，其他城市与之有较大差距，GDP不及其零头，与之没有可比性。因此，选择经济发展水平相近且GDP排名靠前的10个城市为例，这样比较才更有现实意义［8］。

以四川省这10个城市为研究对象。第三产业占比越大，表明经济越发达，固定资产投资越大，表明经济发展的后劲越大，城镇化水平越高，表明经济发展越快，社会消费品零售越大，表明居民购买力越强，经济越发达，人口数量对社会消费品零售额、住户存款有影响。故本研究选择地区生产总值（X1）、第三产业占比（X2）、城镇化率（X3）、固定资产投资（X4）、人口数量 （X5）、财政收入（一般公共预算收入）（X6）、城镇居民收入（X7）、农村居民收入（X8）、社会消费品零售总额（X9）、住户存款（X10）为评价指标，评价这些城市的经济发展水平［9］。这 10个城市有关的国民经济和社会发展统计数据如表1所示。

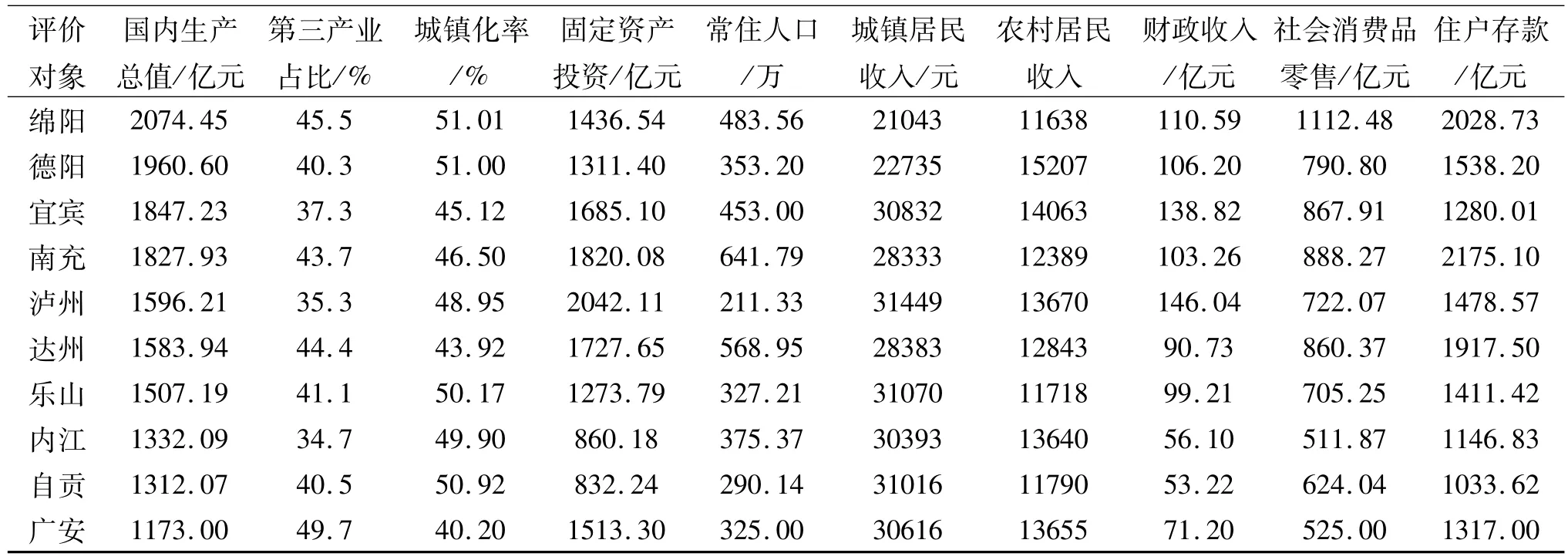
表1 四川省部分城市经济社会发展统计数据

数据规范化。首先消除指标的量纲和方向性。在10个评价指标中，人口数量影响人均GDP、人均存款、人均消费量。其它条件不变的情况下，人口数量越多，则指标数值就越低，因此，它为成本型指标；不难理解，其它指标对经济发展都有正面影响，因此，它们为效益型指标，故 X1、X2、X3、X4、X6、X7、X8、X9、X10为效益型指标，X5为成本型指标，分别按式（3）-（4）规范化，结果如表2所示。

表2 规范化数据

确定指标的权重。根据实际情况和经验，取这10个指标的重要性评分分别为：P1＝10，P2＝9．75，P3＝9．5，P4＝9．25，P5＝8，P6＝8．75，P7＝8．5，P8＝8．25，P9＝8．0，P10＝7．75。根据式（9）求得 10 个评价指标的权重分别为：w1＝0．1227，w2＝0．1098，w3＝0．1070，w4＝0．1042，w5＝0．1014，w6＝0．0896，w7＝0．0958，w8＝0．0930，w9＝0．0901，w10＝0．0874。于是可得到加权规范化数据，结果如表3所示。

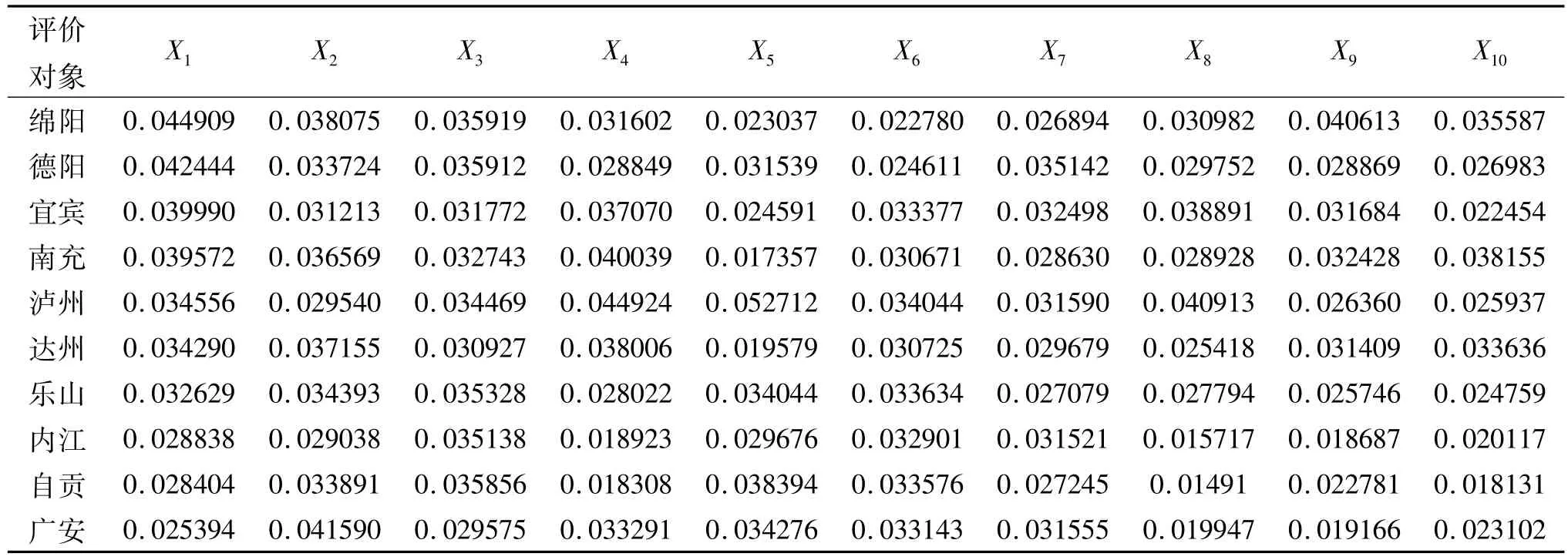
表3 加权规范化数据

然后，将规范化数据按式（5）转换为均值为0，标准差为1的分布，结果如表4所示。

表4 规范化

求指标的相关系数矩阵。结果如表5所示，从表4知，许多指标的相关系数大于0.5，X1与X9最大，达0．89573，说明这些指标存在很强的相关性，适合于运用主成分分析方法。

表5 相关系数矩阵

求相关系数矩阵的特征值、主成分的贡献率、累积贡献率。首先求相关系数矩阵的特征值，然后按式（6）-（7）主成分的贡献率、累积贡献率，结果如表6所示。从表6知，主成分与指标个数相等，一共10个，前几个的贡献率较大，越往后，贡献率越小。

表6 主成分特征值及贡献率

提取主成分。按累积贡献率大于90%提取主成分，从表6可见，提取的主成分只有1、2、3、4个，分别记为 F1、F2、F3、F4，它们的载荷系数如表7 所示。

表7 主成分载荷系数

因此，提取的主成分可表示为：

F1＝0．28528X1＋0．15938X2＋0．43892X3＋0．43793X4-0．35113X5-0．1822X6-0．04751X7-0．27993X8＋0．46819 X9＋0．29211X10；

F2＝-0．30836X1-0．49513X2-0．17814X3＋0．149447X4-0．13001X5-0．10512X6-0．39972X7-0．38671X8-0．00328X9＋0．51843X10；

F3＝0．45954X1＋0．28909X2-0．23495X3＋0．09935X4-＋0．33701X5-0．69126X6＋0．13217X7-0．06182X8-0．11927X9＋0．11293X10。

F4＝-0．20159X1＋0．04122X2-＋0．12038X3-0．12533X4-0．36379X5-0．17917X6＋0．78913X7-0．29309X8-0．15027X9-0．17876X10。

主成分 F1、F2、F3、F4为综合新变量，它们由原10个指标线性组合而成，且线性无关，互不重复，可替代原指标X1、X2、…、X10对评价对象进行评价，并包含了原指标90．8016%的信息。

计算评价对象的综合得分。评价对象的综合得分为提取主成分与对应贡献率积之和，即：

F ＝0．410971F1＋0．206890F2＋0．191093F3＋0．099056F4

由此求得各评价对象的综合得分结果如表8所示，从表7知，泸州市的经济发展水平最好，内江市的经济发展水平最差。评价结果直观图如图1所示。

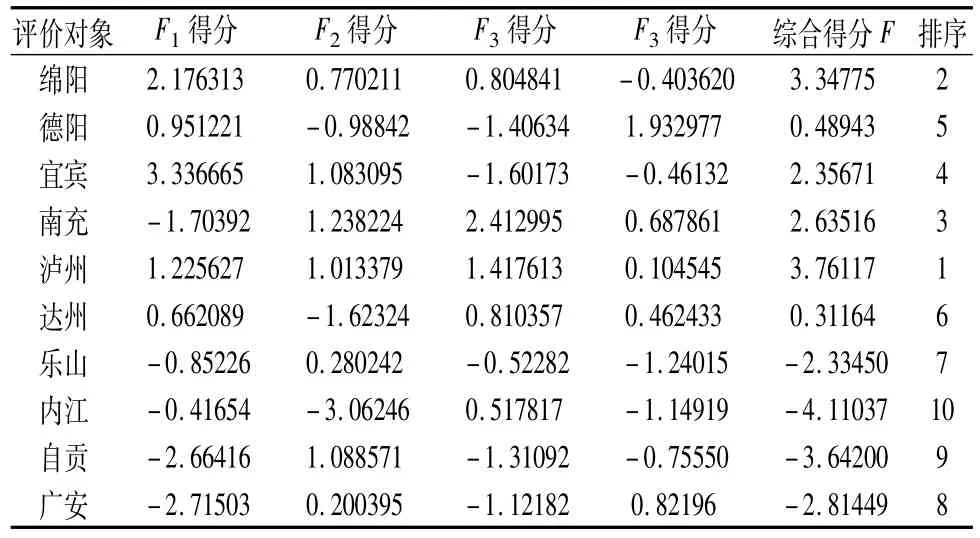
表8 评价对象的综合得分

图1 评价结果直观图

三、结语

区域经济发展不平衡，将会制约我国经济的全面和充分发展，阻碍我国全面小康社会目标的实现，因此，必须采取有效的措施，协调区域经济发展，把改革创新作为第一推动力，推进区域经济的共同发展［10］。首先，经济欠发达地区，要解放思想，改变观念，在体制机制上改革创新，转变政府职能，切实解决政府缺位、错位、越位等问题，加强经济建设，树立自尊自强，不等不靠、自力更生意识，主动作为、真抓实干，创造性地开展工作。其次，经济欠发达地区，要充分利用本地资源优势，合理布置产业结构，扬长避短，走差异化发展道路。选择最具比较优势的产业，充分放大特色产业优势，培育若干各具特色、竞争力强的产业群及产业链，以优势资源带动区域经济的发展。再次，经济欠发达地区，要提高开放水平，加强招商引资，扩大利用外资的规模。政府要增强为企业服务的思想，优化本地区投资环境，简化办事程序，提高办事效率，为外资的引进提供优越、宽松、便捷的环境，形成重商、亲商、安商、旺商氛围。同时，国家要加大对经济欠发达地区的支持，加快欠发达地区的发展。尤其要加大对欠发达地区基础教育的投入，改善欠发达地区的教学设施和教师待遇，加快欠发达地区人力资源开发。采取优惠政策，鼓励和支持优秀教师去落后地区任教支教，为经济欠发达地区的经济发展培养更多的人才。还有，经济欠发达地区，要处理好经济发展与生态环境保护的关系，树立绿水青山就是金山银山的思想，把生态环境保护放在首要位置，把生态优势变为发展优势，积极发展生态经济，以生态文明建设促进区域经济高质量可持续发展。最后，经济发达地区，要树立全局观念，无私帮助经济欠发达地区。要在资金、物质、人才、技术、管理上大力给予支持，以自己的发展经验和发展道路，作好传帮带，不仅要“输血”，也要帮助其“造血”，增强欠发达地区的自我发展能力，促进欠发达地区经济发展的内生动力。

评价区域经济发展水平，对促进区域经济平衡发展，共同走向富裕具有积极的意义。主成分分析是通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，删去重复冗余的变量，建立尽可能少的新变量，所得到的这些新变量是两两不相关的，互不重复，而且它们能保持原有的大部分信息［11］。这样，能将复杂的多项指标转化为少数几个综合指标，使问题的求解简单化，同时又不失真实性，是解决冗杂多变量决策问题的有效工具。文中运用主成分分析法评价四川部分城市经济发展水平，较好地解决了评价指标相关性和评价工作复杂的问题，使评价工作更为便捷高效。对促进我国各地均衡发展、高质量发展、全面发展、可持续发展，早日实现全面建成小康社会的目标具有重要意义。