基于残差修正GM（1，N）的成都市社会消费品零售额预测

王洪平

生产是消费的目的。生产的终极目标是为了满足人们对物质文化生活的需要，不断提高人民的生活水平和质量，促进社会的文明、进步和发展。消费是生产的动力，生产的产品只有被消费者有效消费掉，再生产才能延续和扩大，否则，如果消费不畅或消费萎缩，则势必造成生产者产品积压，资金无法回笼，因缺乏购买生产资料的资金，生产无法延续下去。可见，消费是生产的重要环节，是推动经济发展的重要力量。在我国经济从旧常态向新常态转化的历史阶段，消费在经济发展中具有引领作用，是打开我国经济高质量发展的钥匙。消费目前已成为推动我国经济从高速增长迈向高质量增长的关键要素，积极培植和壮大消费市场，打好扩大内需这张牌，是今后我国经济转型发展的主要突破口，也是解决我国经济发展中出现深层次的问题，尤其是资源环境矛盾，促进物质与生态协同发展、经济社会均衡发展的根本途径。社会消费品零售总额是判断一个国家和地区的内需和消费能力以及经济运行状况的一个重要指标，研究社会消费品零售总额影响因素，对制定宏观经济政策，调整产业结构，贯彻扩大内需政策，积极发展消费经济，保持市场供需平衡，维护经济平稳发展等具有重要意义。

关于社会消费品零售总额预测问题，国内一些学者进行了研究，主要预测方法有：自回归滑动平均模型［1］，多元线性回归［2］，logistic 模型［3］、灰色模型［4］、支持向量机［5］、神经网络等［6］。这些方法都有各自的特点，但也存在一定的不足。灰色GM（1，N）预测模型，反映了（N-1）个变量对某一个变量1阶导数的影响。该模型由于（N-1）个因子的作用，不仅可以反映分析对象本身随时间的动态变化，还可以了解整个系统的变化规律。在工程控制、管理决策和社会经济等许多领域得到了广泛的应用［7］。但如果GM（1，N）模型使用不当，预测效果往往不尽如人意。本研究对GM（1，N）模型进行了多方面的改进，并以城镇居民人均可支配收入，农村居民人均纯收入、地区人口数量、城镇化率为驱动因子，社会消费品零售总额为考察因子，运用修正后的灰色GM（1，N）预测成都市居民社会消费品零售额。

一、灰色 GM（1，N）模型

（一）传统 GM（1，N）模型

灰色GM（1，N）模型用于刻画n个相关联的变量之间的联系和变化，其中，1个变量作为主要考察对象（因变量），其它变量作为驱动因子（自变量），考察变量的变化发展趋势以驱动因子为基础，因变量表示为自变量的指数函数形式，从而实现对考察对象的预测［8］。

对于n个变量：x1，x2，…xn，如果每个量都有 m个相互对应的数据，则可形成n个时间序列Xi（0）（k），即 Xi（0）（k）＝｛xi（0）（1），xi（0）（2），…，xi（0）（m）｝，i＝1，2，…，n；k＝1，2，…，m；其中，x1（0）（k）为系统行为序列，xi（0）（k）为驱动变量，i＝2，3，…，n；k＝1，2，…，m。

对xi（0）进行累加生成n个数列xi（1）＝｛xi（1）（1），xi（1）（2），…，xi（1）（m）｝，

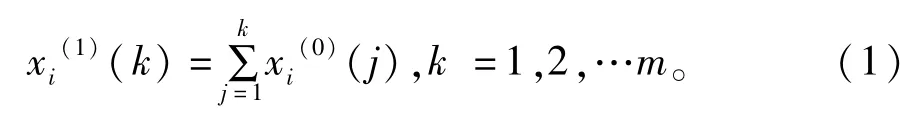
生成x1（1）（k）的紧邻均值序列 Z1（1）（k）＝｛z1（1）（2），z1（1）（3），…，z1（1）（k）｝，k ＝2，3，…m。

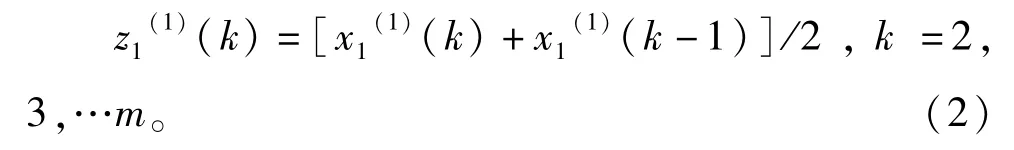
则 GM（1，N）模型为［9］：

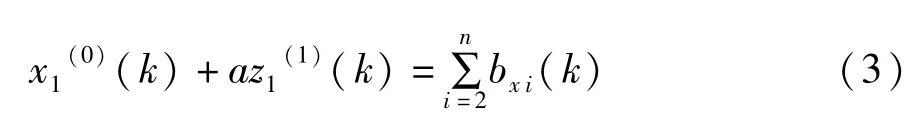
GM（1，N）模型的白化方程为：

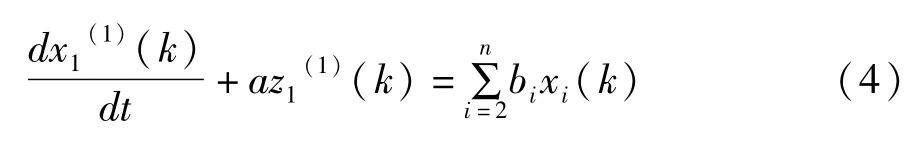
根据最小二乘法，可得到参数列A的估计：

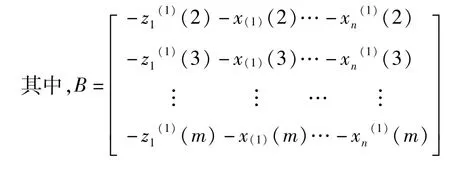
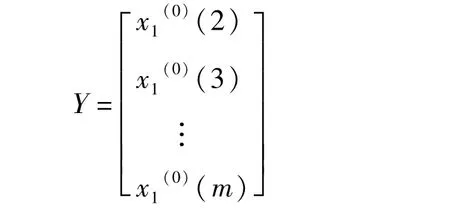
则GM（1，N）模型的近似时间相应为：

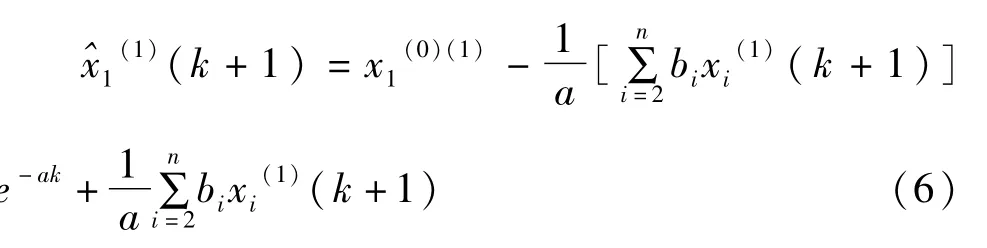
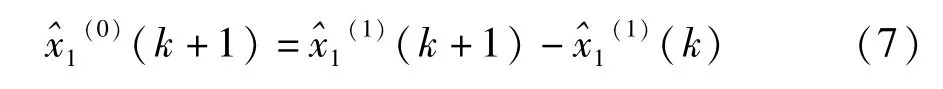
（二）GM（1，N）模型的改进

由于GM（1，N）模型的驱动变量的量纲和数量级不同，影响模型的广泛应用，同时，也难以合理辨别驱动变量对系统行为变量的客观影响。系统行为变量的背景值影响预测精度，传统GM（1，N）模型系统行为变量的背景值为积分函数的近似表达，存在一些误差，影响预测效果［10］。因此，本研究采取对驱动变量进行初始化和对行为变量背景值进行优化的方法对传统GM（1，N）模型进行改进。

1.驱动变量初始化

2.背景值优化

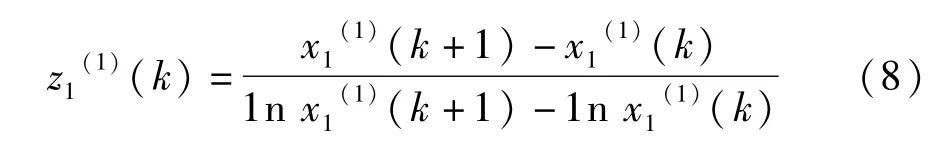
3.残差修正 GM（1，N）模型

残差修正GM（1，N）模型基本思想就是将预测误差再通过一次GM（1，N）模型运算，得到新的预测残差，最后将其加到原预测值中，以提高预测的精度。

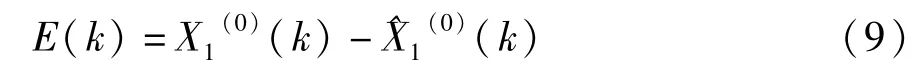
为行为序列的残差。

残差E（k）有正有负，为了便于建模，需要将残差序列全部变为正数，转化为新残差序列E1（k）。

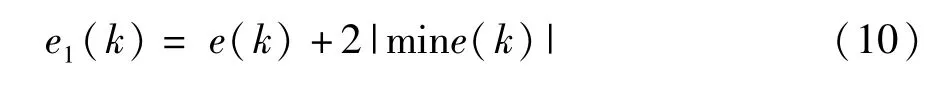
即将残差序列都加上2倍绝对值最小的残差。

虽然新残差序列E1（k）都为正数，但不一定具有单调性，此时还要将其转化为具有单调性的残差序列（单调上升），转化采用波形数据生成法，生成一个与 E1（k）有关的序列 D（k）＝｛d（1），d （2），…，d（m）｝。

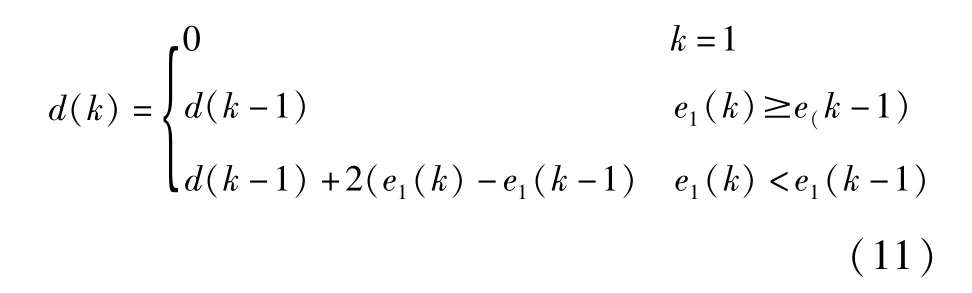
则可得到具有单调性的残差序列E2（k）。

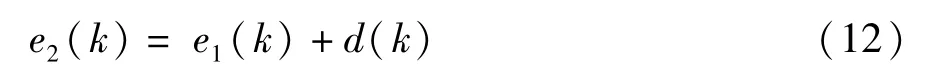
以E2（k）行为序列，驱动变量不变，运用改进的GM（1，N）模型预测 E2（k）值，然后还原为 E（k）的预测值，即：

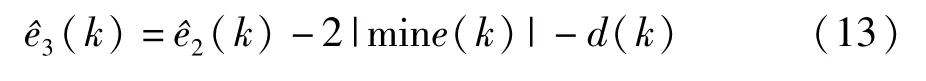
则最终得到残差修正GM（1，N）模型对行为序列X1（0）（k）的预测值。

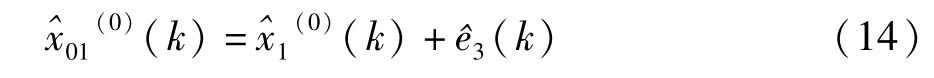
二、成都市居民社会消费品零售额预测

成都市是四川省省会，西南地区唯一一个副省级城市，特大城市，国家重要的高新技术产业基地、商贸物流中心和综合交通枢纽，西部地区重要的中心城市。在国家实施西部大开发战略以来，成都凭借科教、人才、信息等在中西部地区具有得天独厚的优势条件，经济发展迅猛，2017年成都市实现地区生产总值13889.39亿元，在全国副省级城市排名第三，比上年增长了8.1%，高于全国1.2个百分点。人民生活水平不断提高，消费需求旺盛。图1为2007年—2017年成都市社会消费品零售额统计数据（数据来源于成都市统计年鉴），从图1可知，成都市社会消费品零售额从2007年的610.8亿元增长到2017年的2444亿元，增幅达371.81698%，平均年增幅37.18170%，增长速度惊人，充分说明成都市11年来经济社会发展取得了夺目的成绩，居民收入快速增长，人民生活富裕，消费旺盛，有力地推动了成都市经济的持续快速发展。

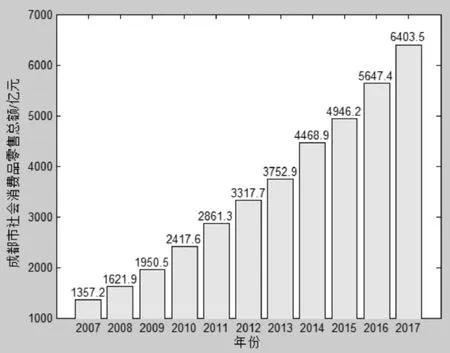
图1 成都市居民社会消费品零售额统计数据

影响社会消费品零售总额的因素较多，有政治方面、经济方面、社会方面，有些因素可以量化，有些因素不能量化，有些因素比较具体，有些因素比较抽象。本着最直接、最有效、可操作、可量化性的原则，本研究选取人口数量、农村居民收入、城镇居民收入、城镇化率为驱动变量，预测社会消费品零售总额变化规律，即社会消费品零售总额为行为序列。

图1为2007年—2017年成都市社会消费品零售总额、城镇居民收入、农村居民收入、人口数量、城镇化率统计数据。

表1 成都市社会消费品零售额、居民收入、人口、城镇化率

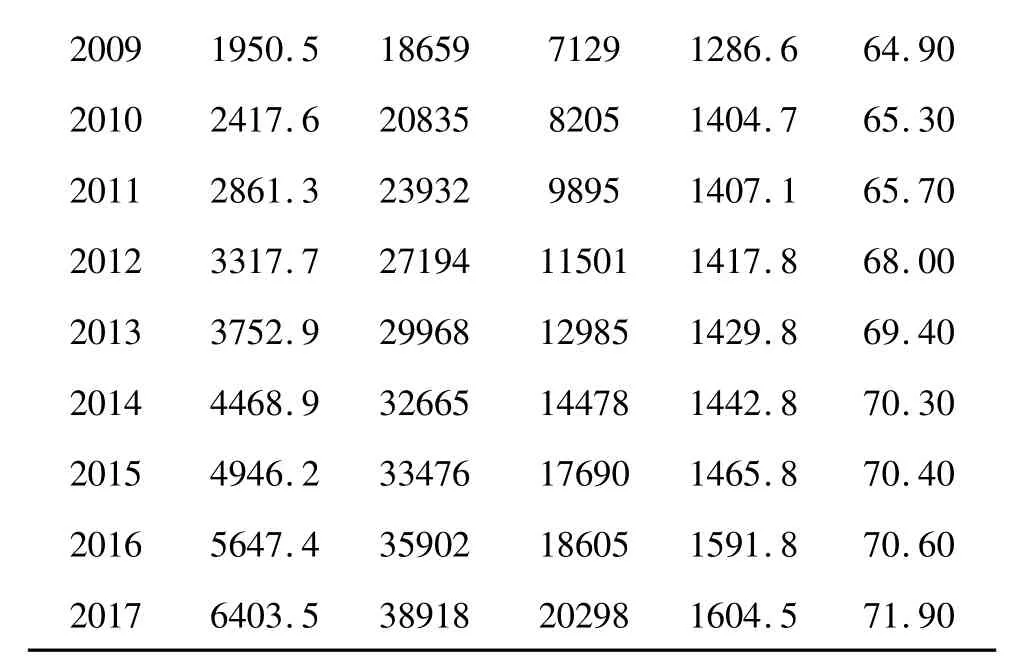
2 0 0 9 1 9 5 0.5 1 8 6 5 9 7 1 2 9 1 2 8 6.6 6 4.9 0 2 0 1 0 2 4 1 7.6 2 0 8 3 5 8 2 0 5 1 4 0 4.7 6 5.3 0 2 0 1 1 2 8 6 1.3 2 3 9 3 2 9 8 9 5 1 4 0 7.1 6 5.7 0 2 0 1 2 3 3 1 7.7 2 7 1 9 4 1 1 5 0 1 1 4 1 7.8 6 8.0 0 2 0 1 3 3 7 5 2.9 2 9 9 6 8 1 2 9 8 5 1 4 2 9.8 6 9.4 0 2 0 1 4 4 4 6 8.9 3 2 6 6 5 1 4 4 7 8 1 4 4 2.8 7 0.3 0 2 0 1 5 4 9 4 6.2 3 3 4 7 6 1 7 6 9 0 1 4 6 5.8 7 0.4 0 2 0 1 6 5 6 4 7.4 3 5 9 0 2 1 8 6 0 5 1 5 9 1.8 7 0.6 0 2 0 1 7 6 4 0 3.5 3 8 9 1 8 2 0 2 9 8 1 6 0 4.5 7 1.9 0

设成都市社会消费品零售额、城镇居民人均可支配收入、农村居民人均纯收入、人口数量、城镇化率的时间序列分别为：x1（0）（k）、x2（0）（k）、x3（0）（k）、x4（0）（k）、x5（0）（k），则

x1（0）（k）＝［1357．2，1621．9，1950．5，2417．6，2861．3，3317．7，3752．9，4468．9，4946．2，5647．4，6403．5］；

x2（0）（k） ＝［14849，16943，18659，20835，23932，27194，29968，32665，33476，35902，38918］；

x3（0）（k）＝［5642，6481，7129，8205，9895，11501，12985，14478，17690，18605，20298］；

x4（0）（k）＝［1257．9，1270．6，1286．6，1404．7，1407．1，1417．8，1429．8，1442．8，1465．8，1591．8，1604．5］；

x5（0）（k）＝［63．00，63．58，64．9，65．3，65．7，68，69．4，70．3，70．4，70．6，71．9］。

首先对x2（0）（k）、x3（0）（k）、x4（0）（k）、x5（0）（k）进行初始化处理，于是有：

y2（0）（k）＝［1．0，1．14102，1．256583，1．403125，1．611691，1．831369，2．018183，2．199811，2．254428，2．417806，2．620917］；

y3（0）（k）＝［1．0，1．148706，1．263559，1．454272，1．753811，2．038462，2．301489，2．566111，3．135413，3．29759，3．59766］；

y4（0）（k）＝［1．0，1．010096，1．022816，1．116702，1．11861，1．127117，1．136656，1．146991，1．165275，1．265442，1．275539］；

y5（0）（k）＝［1．0，1．009206，1．030159，1．036508，1．042857，1．079365，1．101587，1．115873，1．11746，1．120635，1．14127］。

以x1（0）（k）、y2（0）（k）、y3（0）（k）、y4（0）（k）、y5（0）（k）为样本，建立灰色 GM（1，5）模型，利用 matlab 工具求得参数列估计值为：

即：a＝0．61166，b2＝5317．64530，b3＝-4593．64749，b4＝-1940．71445，b5＝1761．43814；由此可得到成都市社会消费品零售额的时间相应式为：

进行一次累减，得到成都市社会消费品零售额的预测值，结果如表2所示。

计算残差序列，结果为：

E（k）＝［0，175．8802，-597．391，-760．1934，-826．3877，-770．2357，-707．3465，-383．9502，-1100．99，-719．9136，-453．5895］。

将残差序列转化为正数序列，结果为：

E1（k）＝［2202．0，2377．9，1604．6，1441．8，1375．6，1431．7，1494．6，1818．0，1101．0，1482．1，1748．4］。

计算波形数据转化参考序列，结果为：

D（k）＝［0，0，1546．542，1872．147，2004．536，2004．536，2004．536，2004．536，3438．615，3438．615，3438．615］。

计算单调性残差序列，结果为：

E2（k）＝［2201．98，2377．86，3151．13，3313．93，3380．13，3436．28，3499．17，3822．57，4539．61，4920．68，5187．01］。

以 e2（k）、y2（0）（k）、y3（0）（k）、y4（0）（k）、y5（0）（k）为样本，建立灰色GM（1，5）模型，利用matlab工具求得参数列估计值为：

即：a1＝061166，b12＝5317．64530，b13＝-4593．64749，b14＝-1940．71445，b15＝1761．43814。由此可得到残差的时间相应式为：

进行一次累减，得到残差序列的预测值，结果为：

Ê2（k）＝［2201．98，2359．501，4002．625，4294．775，4421．79，4536．281，4549．408，4469．376，7129．426，5922．495，5978．951］。

最后进行逆操作运算操作得到残差的实际预测值，结果为：

Ê2（k）＝［0，157．521，254．1028，220．6478，215．2741，329．7646，342．892，262．8605，1488．83，281．8999，338．3557］。

将先前的预测值和残差预测值相加，最终得到行为序列的预测值，结果如表2所示。

表2 预测结果及比较

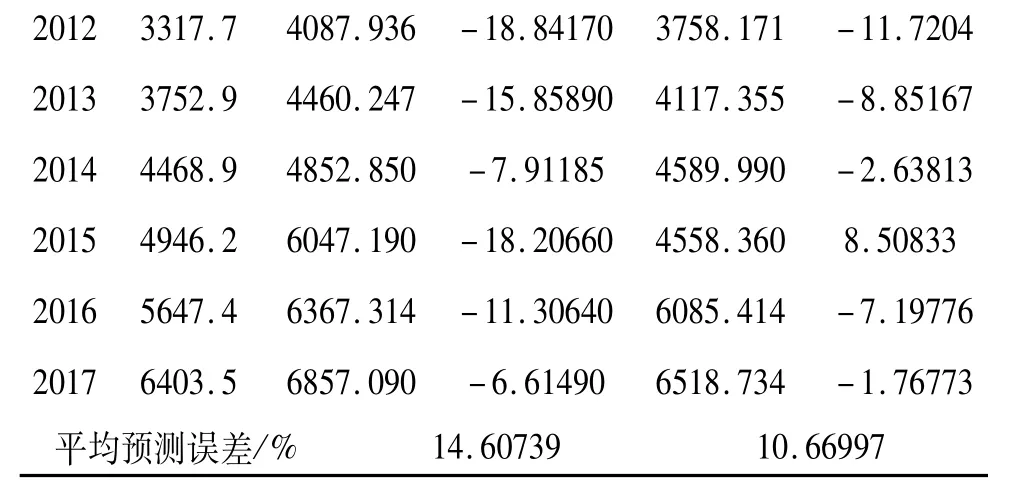
2012 3317.7 4087.936 -18.84170 3758.171 -11.7204 2013 3752.9 4460.247 -15.85890 4117.355 -8.85167 2014 4468.9 4852.850 -7.91185 4589.990 -2.63813 2015 4946.2 6047.190 -18.20660 4558.360 8.50833 2016 5647.4 6367.314 -11.30640 6085.414 -7.19776 2017 6403.5 6857.090 -6.61490 6518.734 -1.76773平均预测误差／% 14.60739 10.66997

从表2可见，GM（1，N）模型的平均预测误差为14.60739%，残差 GM（1，N）模型的平均预测误差为10.66997%，残差 GM（1，N）模型的平均预测误差比GM（1，N）模型的平均预测误差减小了26.95499%，看起来误差不小，但残差修正GM（1，N）模型的误差主要为前期贡献，后期误差精度越来越高，2017年的预测误差小于2.0%，而预测模型的价值在于对将来未变化趋势进行准确预判，前期数据仅用于建模，误差大小无关紧要，后期预测误差才是衡量模型优劣的重要指标。前期之所以误差较大，这是模型为了提高后期的预测精度自我调整的结果。从这两个方面来看，残差 GM（1，N）模型还是有比较大的优势。两种模型的预测结果对比如图2所示。

此外，根据驱动系数的大小，我们还可以分析各驱动因子对成都市社会消费品零售总额的影响程度，由于b2＞b5＞b4＞b3，因此，对成都市社会消费品零售总额影响由大到小的因素为城镇居民人均可支配收入、城镇化率、人口数量、农村居民人均纯收入。城镇居民人均可支配收入影响最大，农村居民收入影响最小。这与成都市经济社会发展情况基本吻合。城镇居民收入比农村居民收入大，2017年，成都市城镇居民收入是农村居民收入的1.9173倍，城镇居民有一定的消费基础，目前属于消费提档升级，主要为品质型、个性化、享受型消费，商品价值高，加之城镇居民消费观念新，不仅有当前消费，还有超前消费，因此，城镇居民收入对社会消费品零售额影响最大，而农村居民消费基础差，大多属于生存型消费，以生活必备品的消费为主，商品价值低，再加上农民消费观念陈旧，生活方式节俭，喜欢存钱，为省钱尽量压缩开支，所以农村居民收入对社会消费品零售额影响最小。两种模型的预测曲线如图2所示。

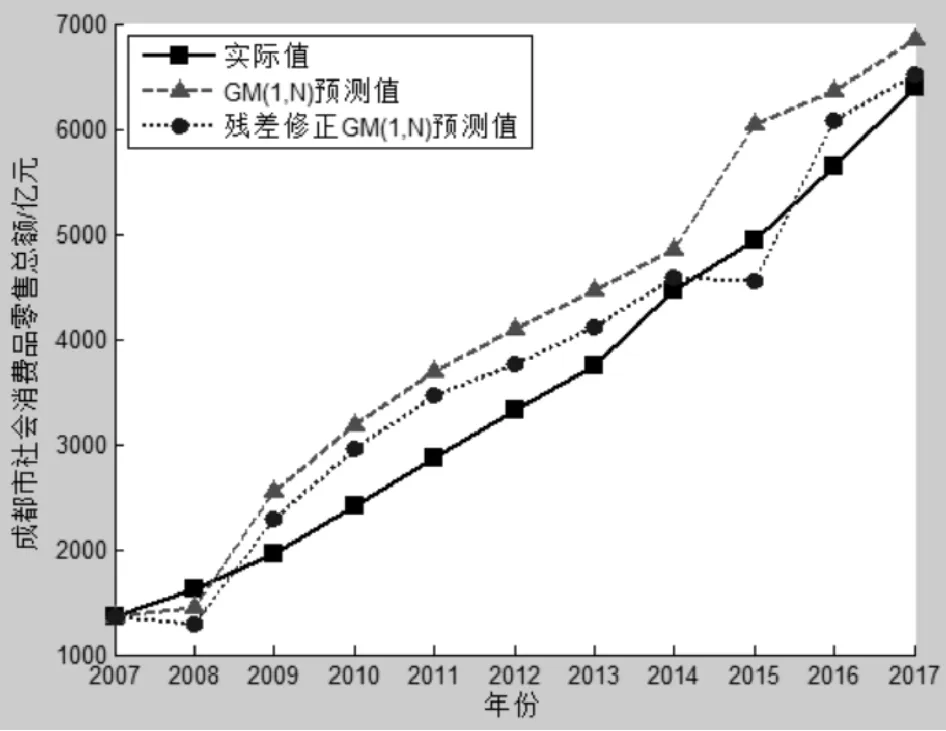
图2 成都市社会消费品零售额预测曲线

三、讨论

在我国经济从高速发展向高质量发展转化的历史阶段，消费在经济发展中具有无可替代的地位，是推动经济持续发展的生力军。积极培植消费市场，认真贯彻落实扩大内需的政策方针，是今后我国经济转型发展的主要方向。促进消费必须从以下几个方面入手：第一，保证居民收入的稳固增长。要建立职工工资与经济增长相适应增长的长效机制，降低个体劳动者的赋税，大力推进乡村振兴工程，促进农民增收致富；第二，健全社会保障体系。要完善养老保险、医疗保险、失业保险等社会保障制度，提高社会保障的覆盖面和保障水平，消除老百姓的后顾之忧，让老百姓敢于花钱、放心花钱。第三，营造良好的消费环境。要加强市场监督管理，严厉打击制假售假行为，维护消费者的利益，维护食品安全卫生，让老百姓用得放心、吃得放心。第四，丰富商品和服务，提高产品质量和服务水平。要以市场为导向，开发适销对路的产品和服务，不断提高产品和服务的质量，使民众对国货有信心，喜欢上中国造，爱上中国造。第五，畅通消费渠道。要合理布局商业零售网点，方便民众购物，积极搭建电商平台，拓宽销售渠道，让消费者能在线上线下自由选择消费。第六，积极创造消费条件。要出台相关政策措施，引导金融等机构为大众消费提供优越的条件和服务，采取消费贷款、分期付款等灵活多样的方式，鼓励消费者超前消费。总之，要不断优化消费环境，增强消费者的信心，保证商品的质量，让消费成为经济增长不竭的动力。

消费是经济增长的“稳定器”和“压舱石”。中国人口众多，中国经济经过几十年持续高速发展，不仅面貌发生了翻天覆地的变化，人民生活也逐步富裕，盼望提高生活质量和品质，有着巨大的消费市场和消费潜力。尤其是广大农村，消费底子还很薄弱，随着新农村建设的快速推进，巨大的市场等待我们去挖掘。今后，在经济建设中要突出消费在经济发展中的重要地位，积极调整需求结构，转变经济发展方式，经济增长要从过度依赖投资和出口转变到消费、投资、出口协调拉动，增强消费对经济增长的拉动作用，增强中国经济的抗外部干扰能力、韧性和活力，让居民消费成为助推中国经济腾飞的翅膀。

四、结语

社会消费品零售总额揭示了国内消费品零售市场的变动规律，反映了国内宏观经济运行状况的好坏，同时揭示了社会总需求和总供给之间的变化情况。一个地区社会消费品零售总额的大小，在一定程度上能体现其市场的繁荣状况，居民购买能力和消费水平的高低。在经济新常态下，合理的消费是保持经济高速和高质量发展的核心。各地必须高度重视消费在经济发展中的重要性，坚持消费在经济中的引领作用，倡导消费者优先的原则。抓住居民消费升级契机，努力增加高品质产品和服务供给，满足消费者不断提高的消费要求，大力培育新兴消费，不断激发潜在消费。树立消费者主体意识，加大消费者合法权益保护力度，提升消费者获得感、幸福感、安全感。研究社会消费品零售总额变化趋势和影响因素，对进行消费体制改革，调整产业结构，促进有效消费，满足人民群众日益增长的对美好生活的追求，实现新旧动能转换，保持国民经济健康运行，促进物质文明、精神文明，生态文明建设等具有重要意义。

GM（1，N）模型是考察（N-1）个变量对某一个变量关系和影响的预测模型。由于（N-1）变量量纲不同，应用受到一定的限制，本课题对传统的GM（1，N）模型提出了多项改进，并以城镇居民人均可支配收入，农村居民人均纯收入、地区人口数量、城镇化率为自变量，社会消费品零售额为因变量，运用改进的灰色GM（1，N）模型预测成都市社会消费品零售额，取得了较好的效果：平均预测误差为10.66997%，比非残差修正的灰色GM（1，N）模型的平均预测误差14.60739%减小了26.95499%，近期预测误差更小，2017年预测误差仅为1.76773%。研究还发现，对成都市社会消费品零售额影响由大到小的因素为城镇化率、城镇居民人均可支配收入、地区人口数量、农村居民人均纯收入等。