纯钒在冲击加载下的动态拉伸断裂和弹性波衰减特性*

李雪梅，俞宇颖，胡昌明，张祖根，彭建祥，王 为

(中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳 621999)

钒具有熔点高、延展性好、高温强度高的特点，被广泛应用于航天、医药等领域，是铁、钛等多种合金材料的重要添加元素。同时，由于具有中子辐照活性低、抗辐照肿胀能力强、与液态金属锂相容性好的优点，纯钒是国际热核聚变反应堆第一壁的重要候选结构材料[1-2]。

已有的静态和准静态实验研究表明，纯钒的力学性能强烈依赖于材料纯度和制备方法，初始微结构差异对其屈服强度、断裂强度和断裂韧性等力学性能具有重要影响[2-7]。同时，材料的力学特性往往与加载压力和加载应变率密切相关，而当前对纯钒动态冲击性能的研究较少，且以低压冲击下的流动特性[8-12]、高压冲击相变[13-14]为主。近几年来，高应变率下纯钒的变形和动态断裂已引起学术界的重点关注。例如，Zaretsky等[15]、Kanel等[16]针对纯钒在平板冲击和斜波加载下的弹性波衰减特性开展了实验研究，分析了温度对纯钒屈服强度和层裂强度的影响；Saveleva等[17]采用化爆加载分析了纯钒的弹塑性衰减特性及层裂断裂对应变率的依赖性；Ashitkav等[18]则利用超短激光脉冲研究了高应变率下纯钒的损伤断裂。上述研究为纯钒在动压高应变率环境下的应用提供了重要依据，但缺乏不同材料制备方法下纯钒的高应变率响应特性的比较研究。

本文中，以热等静压法(hot isostatic pressing, HIP)制备的国产纯钒为研究对象，采用一维平板撞击技术和激光干涉测速技术对冲击加载下纯钒的动态拉伸断裂开展实验研究，分析加工工艺、应变率对纯钒动态拉伸断裂的影响；此外，通过对弹塑性加载速度剖面的分析，给出纯钒弹性前驱波的衰减规律。

1 实验原理及材料参数

实验原理见图1，以∅100 mm口径的一级轻气炮为加载平台，采用对称碰靶方式，使纯钒飞片以预定的弹速撞击纯钒样品，在飞片和样品内分别产生左行和右行弹塑性加载波。它们分别到达飞片后界面和样品自由面后，经反射在样品内产生相向传播的两簇中心稀疏波，两者在样品内相遇后产生拉应力区。当拉伸应力幅值足够大，则样品将发生层裂，并在层裂断面处形成新的自由面，使样品自由面速度发生回跳，形成回跳层裂信号。利用激光干涉测速技术DISAR(displacement interferometer system of any reflector)[19]监测弹速和纯钒样品的自由面速度历史，便可以获得纯钒的层裂强度和冲击Hugoniot参数，分析纯钒的弹性波衰减效应。

纯钒试样与文献[13-14]中的为同批次，采用粉末冶金工艺，由热等静压法(HIP)制备而成(以下简称HIP纯钒)，其平均晶粒尺寸小于70m，纯度为99.93 %，主要杂质成分及含量见表1。纯钒的密度为6.104 g/cm3，实测零压纵波声速和剪切波速分别为cL=6.053 km/s和cs=2.770 km/s，由此得到其零压体波声速cb=5.139 km/s，泊松比ν=0.364。实验采用两种不同的飞片厚度，以分析不同拉伸应变率对纯钒层裂强度的影响。

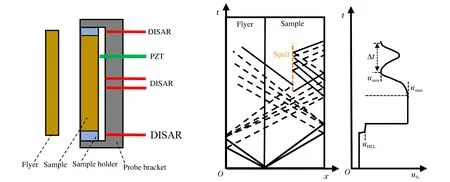
图1 层裂实验装置及实验原理Fig.1 Schematic of the experimental configuration

杂质元素a)CNOAlFeCrSi质量分数/%0.00520.00260.0200.016<0.005<0.0050.018

注：a) 除Al和Si外，其余杂质含量均优于GB4310-84≪钒≫中V-1牌号熔炼钒的指标。

2 实验结果及分析

2.1 实验参数和主要结果

表2 纯钒对称碰撞层裂实验参数及结果Table 2 Summary of experimental parameters

注：a)括号内的值为不考虑回跳速度修正得到的层裂强度。

图2为HIP纯钒的自由面速度剖面测量结果汇总。由图2可以看出：在加载段，波剖面具有典型的弹性波-塑性波双波结构；在卸载段，由两相向传播的稀疏波相互作用引起的层裂回跳信号特征明显。

图2 纯钒的自由面速度剖面汇总Fig.2 Measured free-surface velocity profiles of HIP vanadium at different impact velocities

2.2 纯钒的动态拉伸断裂特性

利用图2所示的自由面速度剖面数据, 便可以计算纯钒的层裂强度σsp。由于平板撞击下加载波为梯形脉冲，样品和层裂片内的弹塑性波及其相互作用将导致速度剖面畸变，使得由σsp=ρ0cbΔufs/2计算得到的层裂强度偏离真值。为此，本文采用下式给出的层裂强度公式计算σsp，以计入材料弹塑性特性效应引入的回跳速度修正[21]：

(1)

层裂强度σsp对应的平均拉伸应变率为：

(2)

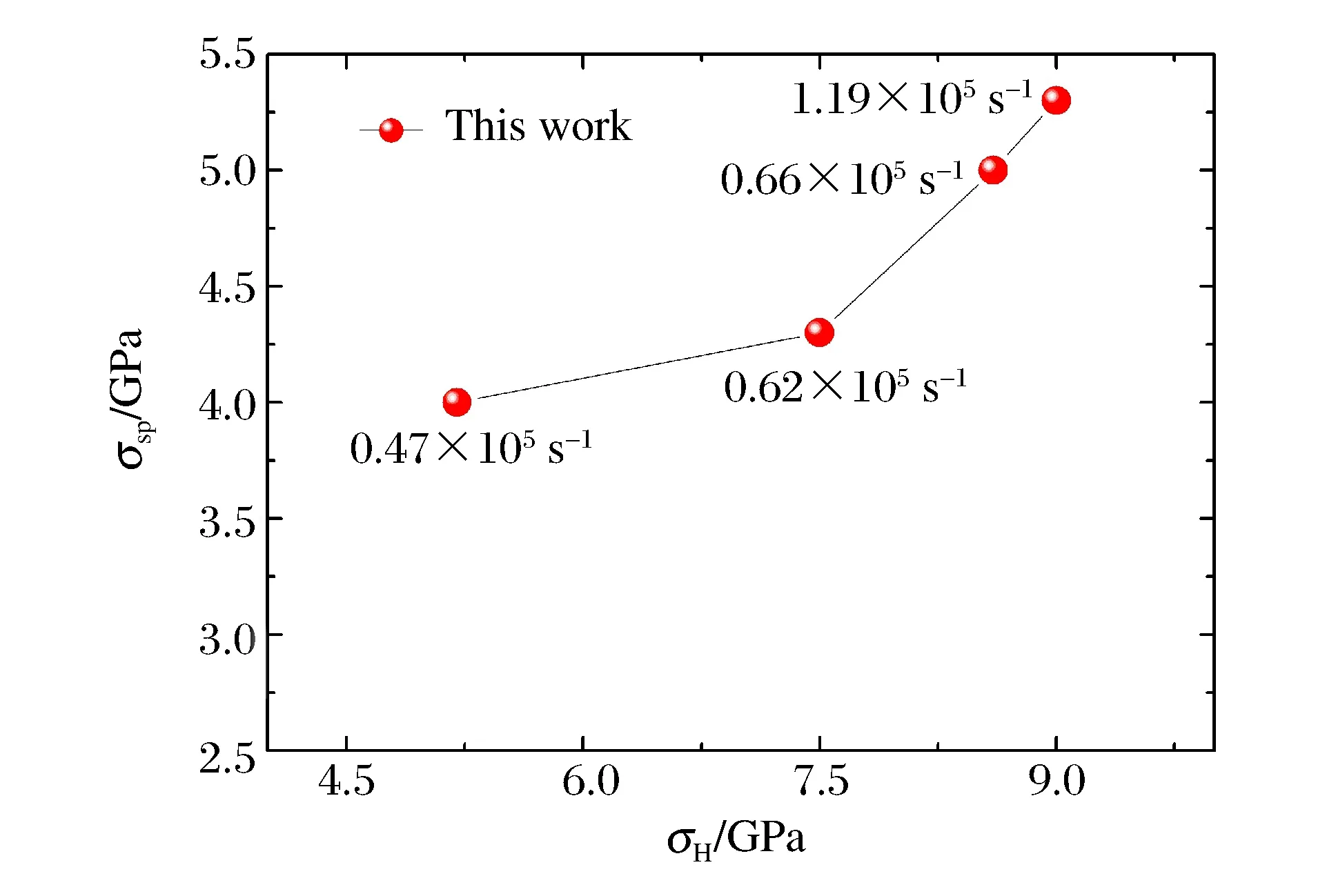
图3 HIP纯钒层裂强度随加载压力和应变率的变化关系Fig.3 The dependence of spall strength for vanadiumon shock pressure and tensile strain rate

图4 不同实验给出的纯钒层裂强度比较Fig.4 Comparison of spall strengths obtainedby different experiments for pure vanadium

从表2可以看出，在一维平面冲击加载下，国产HIP纯钒具有较强的抗拉伸断裂能力，计入材料弹塑性特性导致速度剖面畸变引入的速度修正时，其层裂强度高达4.0～5.3 GPa。同时，纯钒的层裂强度对冲击压力和拉伸应变率均比较敏感。从实验No.1～No.3的结果来看，在平均拉伸应变率变化不大的情况下，冲击压力从5.2 GPa升高到8.6 GPa时，纯钒的层裂强度升高了1 GPa；而比较实验No.3和No.4发现，虽然冲击压力十分接近，但当拉伸应变率从0.66×105s-1升高到1.19×105s-1时，纯钒的层裂强度也升高了0.3 GPa。本文HIP纯钒层裂强度对压力和应变率的依赖关系见图3。纯钒层裂强度对应变率的依赖性在文献[15]和[17]中也有报道。这两篇文献采用与本文相同的层裂强度计算方法，前者在1.5×105～5.1×105s-1(平板冲击加载)应变率下得到的纯钒层裂强度在2.6～3.9 GPa范围，后者在～107s-1(化爆加载)应变率下得到的层裂强度升高至～6.4 GPa，高应变率的影响更明显。图4直观地给出了不同应变率实验下纯钒的层裂强度汇总。

此外，从图4可以看出，在相近加载条件下(平板冲击)，本文HIP纯钒的层裂强度明显高于Zaretsky等[15]给出的熔炼纯钒实验结果，在～105s-1应变率下平均相差～1.3 GPa。上述差别的原因可以归结于不同加工工艺下材料初始缺陷的差异。一方面，图2中较光滑的速度回跳信号显示出纯钒韧性断裂的典型特征，其损伤演化是在拉伸脉冲作用下孔洞成核、长大和聚合的过程。另一方面，与熔炼法纯钒相比，本文中采用HIP法制备的纯钒纯度较高(>99.93%)，晶粒较细(晶粒大小<70m)，组织更均匀，钒基体晶界结合更紧密，影响其力学性能的内缺陷(特别是晶间孔隙)更少。上述原因使得HIP纯钒损伤成核较困难，导致其抗动态拉伸断裂的能力更强。

总体看来，HIP纯钒具有较强的抗动态拉伸断裂能力，其层裂强度对冲击压力和拉伸应变率均比较敏感。

2.3 纯钒的弹性波衰减特性

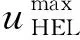
图6 纯钒的Hugoniot弹性极限随样品厚度的衰减规律Fig.6 Decay of elastic wave with sample thickness for pure vanadium

为了更好地分析纯钒的弹性波衰减特性，图6给出了Hugoniot弹性极限随样品厚度变化的现有实验数据汇总。初步看来，尽管s材料制备工艺不同，但本文中所得到的3、6 mm厚HIP纯钒样品的Hugoniot弹性极限与文献[15]和[20]中给出的2.5～5.0 mm范围内的熔炼纯帆实验结果整体趋势一致，材料制备工艺对纯钒Hugoniot弹性极限的影响并不明显。

从图6可以看出，纯钒的弹性前驱波幅值σHEL在样品厚度低于2 mm时的衰减较显著；当样品厚度大于2 mm后，样品厚度对σHEL的影响逐渐减弱，至hs>6 mm后趋于稳定。对图6中的全部实验数据采用指数衰减函数进行拟合，得到其最佳拟合方程为：

σHEL=3.246(hs/h0)-0.386hs≤6 mm

(3)

式中：h0为单位长度。为便于比较，图6中同时给出了Zaretsky等[15]由0.25 mm≤hs≤2 mm范围内的纯钒实验数据拟合得到的对数衰减曲线,σHEL=3.2-1.74 ln(hs/h0)。由图6可以看出，两种拟合曲线在hs≤2 mm内基本一致；本文中给出的指数衰减函数式(3)对于0 mm≤hs≤6 mm范围内纯钒的弹性波衰减特性均可以较好地进行描述；而Zaretsky等[15]给出的对数衰减函数仅能描述2 mm厚度范围内纯钒弹性波幅度的快速松弛，随着样品厚度的增大，该曲线与实验结果偏离越来越大，使用时需要谨慎。

3 结 论

纯钒的动态冲击响应特性与材料加工工艺密切相关。本文中采用平板冲击加载技术，实验获得了国产热等静压(HIP)纯钒在冲击压力5.2～9.0 GPa、拉伸应变率0.47×105～1.19×105s-1的层裂强度, 并对其弹性波衰减特性进行了分析。主要结论如下：

(1)国产HIP纯钒具有较强的抗动态拉伸断裂能力，一维平板加载下其层裂强度位于4.0～5.3 GPa范围，明显高于相似加载条件下文献给出的熔炼钒实验结果。分析认为这与热等静压加工工艺下纯钒杂质含量低、内缺陷(特别是晶间孔隙)较小、钒基体晶界结合更为紧密有关；

(2)纯钒层裂强度对冲击压力和拉伸应变率均比较敏感。冲击压力从5.2 GPa升高到8.6 GPa时，纯钒的层裂强度升高了1 GPa；而在相近压力下，当拉伸应变率从0.66×105s-1升高到1.19×105s-1时，纯钒的层裂强度也升高了0.3 GPa。随着应变率的升高，纯钒层裂强度对应变率的依赖性更显著；

(3)纯钒的弹性波幅值随样品厚度增大而逐渐衰减。在6 mm样品厚度范围，其雨贡纽弹性极限σHEL随样品厚度hs的衰减规律可采用指数函数σHEL=3.246 (hs/h0)-0.386较好地近似，其中h0为单位长度。