破片撞击起爆柱面带壳装药的临界速度修正判据*

王 昕，蒋建伟，王树有，门建兵

(北京理工大学爆炸科学与技术国家重点实验室,北京 100081)

采用高速破片对来袭弹药进行可靠引爆是有效拦截的重要手段。其问题实质则是破片对带壳装药的冲击起爆问题。学者们针对这一问题已进行了广泛的研究，大多以破片冲击平面带壳装药的简化模型为基础开展分析，包括不同材质、形状破片[1-3]对不同厚度壳体、炸药冲击起爆的影响规律，以及建立的诸多半经验的起爆判据，如著名的Held经验判据[4]、Jacobs-Roslund经验准则[5]、Picatinny冲击引爆解析计算式[6]及非均相炸药起爆判据[7]等。也有学者对经典判据的适用条件进行补充修正，包括张先锋等[8]依据Held[9]起爆裸装药的射弹临界速度计算模型，得到射弹起爆带壳装药判据[9]；方青等[10]以Jacobs-Roslund准则为基础，将该准则向斜碰撞上扩展；陈卫东等[11]则推导了不同材质破片冲击起爆屏蔽装药的理论判据等。这些判据能较好预测平面带壳装药的冲击起爆。而实际应用中导弹战斗部多为圆柱形，杜茂华等[12]提到战斗部壳体曲率会影响毁伤元对带壳装药的冲击起爆。已有的数值模拟初步结果也表明，柱面带壳装药与平面带壳装药的冲击起爆特性存在差异[13]。基于平面带壳装药模型的判据已无法准确描述破片对实际弹药的冲击起爆，因此研究适用于柱面带壳装药的临界起爆速度判据非常必要。

本文中采用AUTODYN-3D数值计算软件，对球形破片以不同入射角起爆柱面带壳装药(简称柱壳装药)问题进行数值计算。在对数值模拟数据分析的基础上，通过建立入射角、柱壳装药形状系数的修正因子，得到基于Picatinny工程判据的柱壳装药临界起爆速度修正判据，并与已有的实验数据和数值模拟结果进行对比，验证该判据的普适性。

1 柱壳装药冲击起爆控制参量分析

现役弹药形状多为圆柱形，将破片对来袭弹药战斗部的相互作用简化为破片对柱壳装药的冲击起爆。图1所示为破片撞击柱壳装药的物理模型图，其中柱壳装药壳体厚度为h，装药曲率半径为r；破片着速为v，入射角为θ。

破片对柱壳装药的冲击起爆与破片、装药壳体、炸药以及两者交汇条件等因素相关，主要影响参量如下：

(1)破片：直径d，长度l，密度ρp，弹性常数Ep、γp，屈服极限Yp，形状系数N1；

(2)壳体：厚度h，密度ρt，弹性常数Et、γt，屈服极限Yt，形状系数N2；

(3)炸药：炸药密度ρe，单位质量炸药释放的化学能Ee，膨胀系数γe；

(4)弹靶相互作用条件：破片入射角θ，攻角β。

因此，带壳装药的临界起爆速度vcr可写成以下函数表达式：

vcr=f(d,l,ρp,Ep,γp,Yp,N1;h,ρt,Et,γt,Yt,N2;ρe,Ee,γe;θ,β)

(1)

选取h、ρe、Ee为基本量，根据量纲分析π定理，对上式进行无量纲化，得到：

(2)

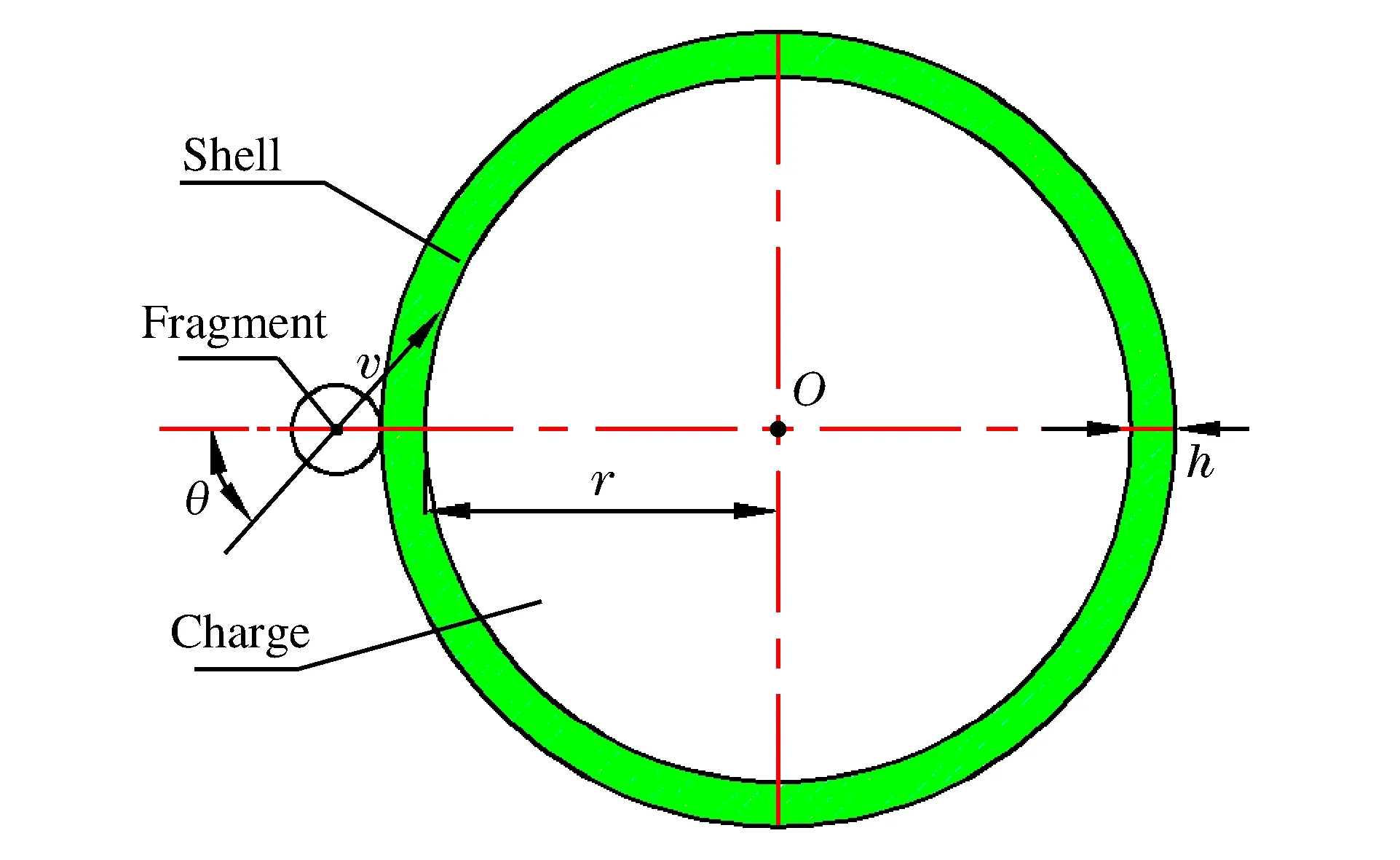
图1 破片对柱壳装药作用剖面Fig.1 Tungsten fragment impact cylindrical shell charge at collision point

在破片和柱壳装药材料不变的情况下，上式可简化为：

(3)

因本文中所研究的破片质量较小，忽略破片尺寸变化引起的冲击起爆阈值的差异，并假定破片与柱壳装药交汇时攻角β=0°，则临界起爆速度值只与破片入射角θ和柱壳装药形状系数N2这2个无量纲函数相关。

无量纲形状系数N2表征柱壳装药的形状对冲击起爆阈值的影响，可用壳体厚度h和曲率半径r组合表示:

(4)

上述分析表明，在壳体厚度保持不变的情况下，对柱壳装药的冲击起爆产生影响的破片入射角θ和装药曲率半径r为相互独立的影响参量。下文中基于此开展修正判据的建立。

2 判据建立

Picatinny工程判据基于屏蔽炸药的敏感系数Kf、屏蔽板厚度h、破片质量m这3个参数建立破片临界起爆速度计算式:

(5)

该式能够较好预测破片垂直撞击平面带壳装药的起爆阈值。本文研究在该工程判据基础上添加入射角和基于曲率半径的柱壳装药形状系数修正项，以期预测破片起爆柱壳装药的临界速度。

在应用中提出如下假设：

(1)Picatinny判据适用于小质量规则破片引发的炸药冲击起爆[14]，不考虑破片形状变化引起的炸药冲击起爆差异；

(2)壳体为钢壳，暂不考虑柱壳装药壳体材质变化引起的炸药冲击起爆差异；

(3)破片运动速度与装药轴线垂直，仅考虑撞击位置的变化引起的入射角的改变；

(4)忽略破片与柱壳装药作用时，装药绕轴心转动引起的临界起爆速度误差。

基于上述假设建立判据修正项，记v0为破片以入射角θ=0°起爆平面带壳装药(r=∞)时的临界速度；定义v(N2,θ)为破片以入射角θ≠0°起爆同等壳体厚度、装药曲率半径r≠∞的柱壳装药临界速度。

定义δ表示破片起爆炸药的临界速度增量，称为修正因子，即：

(6)

变换式(6)得:

v(N2,θ)=(1+δ)v0

(7)

式中:v0采用Picatinny工程判据公式计算，v(N2,θ)则由数值计算获得。

采用入射角θ和柱壳装药形状系数N2来反映破片与柱壳装药交汇条件和柱壳装药结构对临界起爆速度的影响，即δ=f(θ,N2)，因θ、N2相互独立，则δ可表示为：

δ=f(θ)f(N2)

(8)

即

δ=f(θ)f(h/r)

(9)

式中:f(θ)为特定装药曲率半径r*条件下，不同入射角θ时的δ值，即：

f(θ)=δ(r*,θ)

(10)

保持壳体厚度不变，f(h/r)即为特定碰撞角度θ*条件下，不同曲率半径r时的δ值与特定曲率半径r*时δ值之比，即：

(11)

以上为基于Picatinny工程判据应用在柱壳装药上的修正判据建立方法。

3 修正因子获取

式(10)～(11)为构造修正因子函数的方法，为获得具体表达式，针对破片与柱壳装药的作用过程进行数值模拟，采用数据拟合方法得到修正因子函数表达式。

数值模拟采用AUTODYN-3D软件，图2(a)为破片撞击柱壳装药轴对称数值模型，依据典型预制破片战斗部结构，选取破片为质量3g的钨球，柱壳装药，长度80 mm，壳体厚度6 mm，装填Comp-B炸药。图2(b)为钨球、壳体和炸药的离散化网格模型。首先开展网格收敛性及优化工作，考虑CPU机时及计算精度，网格数量选取为2 048、2 800和19 200，采用Lagrange方法开展计算。

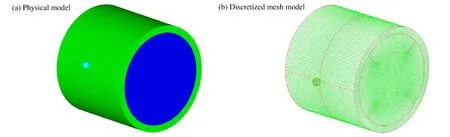
图2 钨球与柱壳装药作用过程的物理及离散化网格模型Fig.2 Physical model and discrete model of tungsten fragment impact cylindrical covered charge

为描述炸药在冲击作用下的起爆过程，其状态方程采用Lee-Tarver[15]状态方程：

(12)

式中:F为燃烧质量份数，它在模拟爆轰过程中控制炸药化学能的释放；参数a是临界压缩度参数；参数I和x为点火量冲击强度及持续函数；参数G1和d控制点火后早期增长函数；参数G2和z为高压反映率相关函数。表1为Comp-B炸药材料模型参数。

表1 Comp-B炸药材料参数Table 1 Material parameters of Comp-B explosive

破片和壳体选用能较好描述材料大应变、高应变率及高温状态的Johnson-Cook强度模型，材料强度模型、状态方程和侵蚀准则列于表2。参数均取自AUTODYN标准数据库。

材料参数的正确与否与计算结果正确性直接相关。采用经典的Picatinny工程判据对已建立的数值模型行验证，表3为2种质量钨球垂直撞击起爆平面带壳B炸药的临界速度数值模拟与理论值的对比。可看出计算值与理论值误差约5%，即认定数值算法的正确性。

表3 临界起爆速度的数值模拟与理论值对比Table 3 Comparison of critical initiation velocities between simulation and theory

为得到柱壳装药受破片撞击后的起爆特性，设计30种工况开展计算，即钨球以入射角θ=0°,15°,30°,45°,55°分别撞击装药曲率半径r=40,60,75,100,200 mm,∞时的柱壳装药。图3所示为典型装药曲率下钨球以v=2 826 m/s，不同θ撞击柱壳装药t=8 μs时刻应力图。可以看出，当v相同时，柱壳装药中的初始传入冲击波及压力随θ的增加而减小，θ=0°时炸药已完全爆轰，而其余入射角条件下无法发生稳定爆轰。而破片撞击起爆不同曲率半径的柱壳装药的过程与平板装药的起爆基本一致，本文中主要从临界起爆速度角度来说明柱壳装药与平面带壳装药的差异。

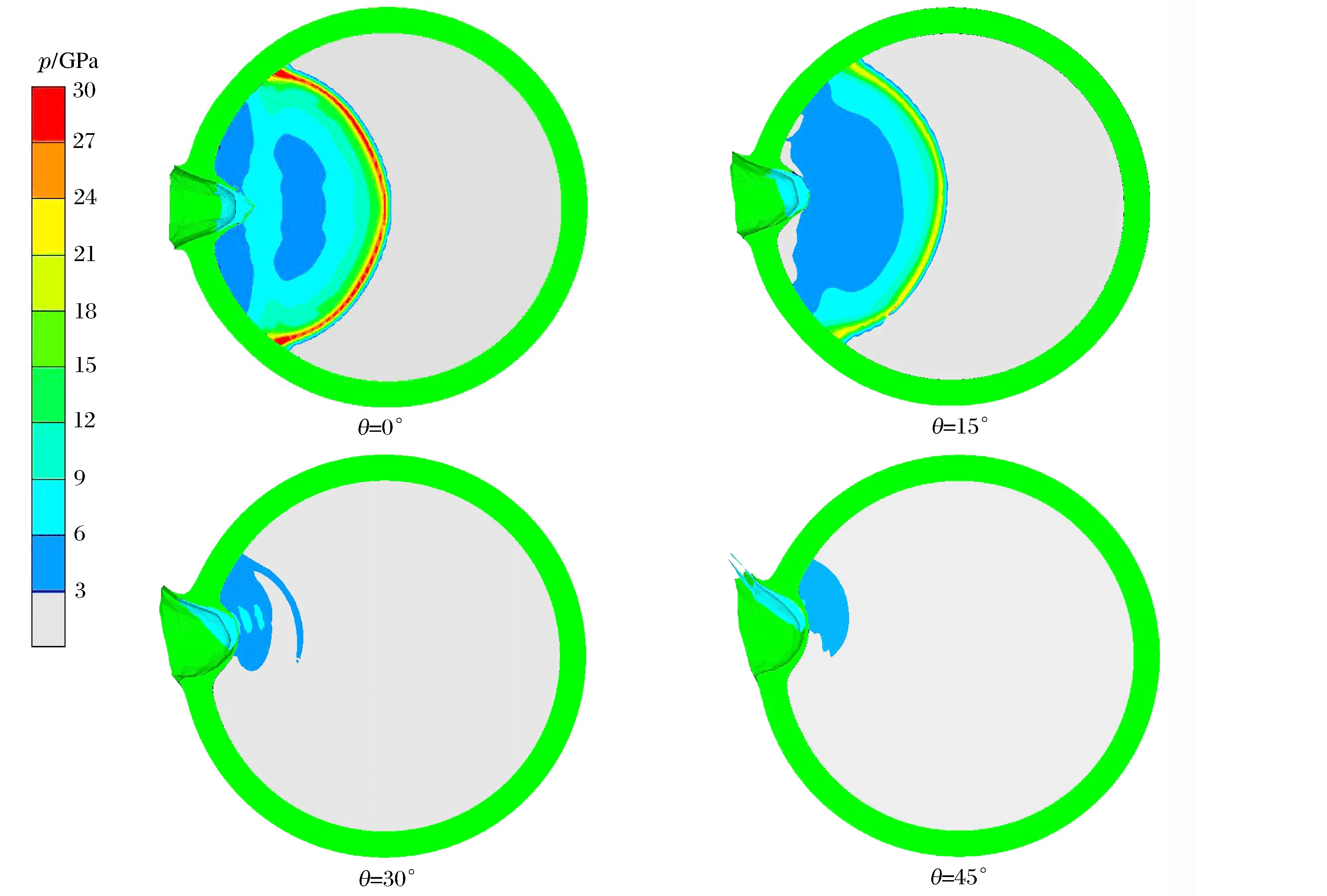
图3 钨球以不同入射角撞击柱面带壳装药应力图Fig.3 Stress of tungsten fragment impact cylindrical shell charge with different incidence angles

采用升降法获得表4中炸药起爆的临界破片速度，对比各临界起爆速度可得出如下结论：

(1)入射角θ对柱壳装药冲击起爆影响较大。临界起爆速度随θ的增大而增加，装药曲率r=40 mm条件下，θ=55°时的起爆速度较θ=0°时增加35.6%，较平面带壳装药增加31.5%。

(2)装药曲率半径r对柱壳装药的冲击起爆有一定影响。除个别点外，临界起爆速度随r增加基本呈现非线性增大，入射角θ=0°条件下，r=∞时起爆速度较r=40 mm时提高3.2%。

在平面和柱壳装药(r=∞、r=40 mm)内距壳体炸药边界4、8、12 mm处设置观测点，编号分别为1、2、3。将破片以入射角θ=0°起爆带壳装药时各观测点的压力进行对比，分析平面与柱壳装药冲击起爆阈值的差异。图4为v=3 000 m/s时观测点的压力时程曲线。冲击波到达平面带壳装药的时间早于柱壳装药，但相同位置处柱壳装药内的压力值高于平面装药。

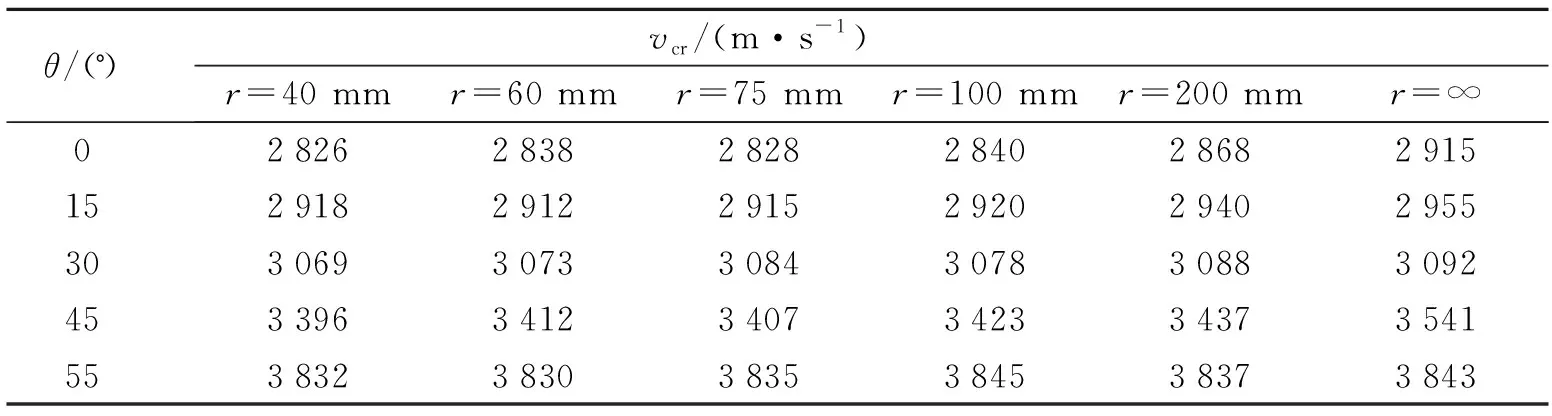
表4 各工况下炸药起爆的破片临界速度Table 4 Critical detonation velocity under various conditions

定性分析柱壳装药冲击起爆速度低于平面带壳装药的原因。破片撞击柱壳装药时，会在壳体和炸药界面处发生波系的反射和透射，在炸药中传入透射波。由于柱壳装药曲率半径小于平面带壳装药，传入的波系会因曲率的存在而发生汇聚。相同撞击条件下、炸药内同一位置处的压力值高于平面带壳装药，因此，起爆柱壳装药易于起爆平面带壳装药。

根据式(6)、(10)～(11)将表4中临界起爆速度进行归一化处理，以获得柱壳装药临界起爆速度修正项，修正项的获取按文献[16]的方法进行拟合。当r=∞(平面带壳装药)时，令f(h/r)=1，此时比较入射角对临界起爆速度的影响，即δ=f(θ)。图5所示为f(θ)随入射角正弦sinθ的变化关系，可以看出，其f(θ)随sinθ的增大呈现指数增加。当入射角度大于55°时破片将发生跳飞，临界起爆速度趋于无限大。进一步通过最小二乘法得出f(θ)随sinθ的变化关系：

(13)

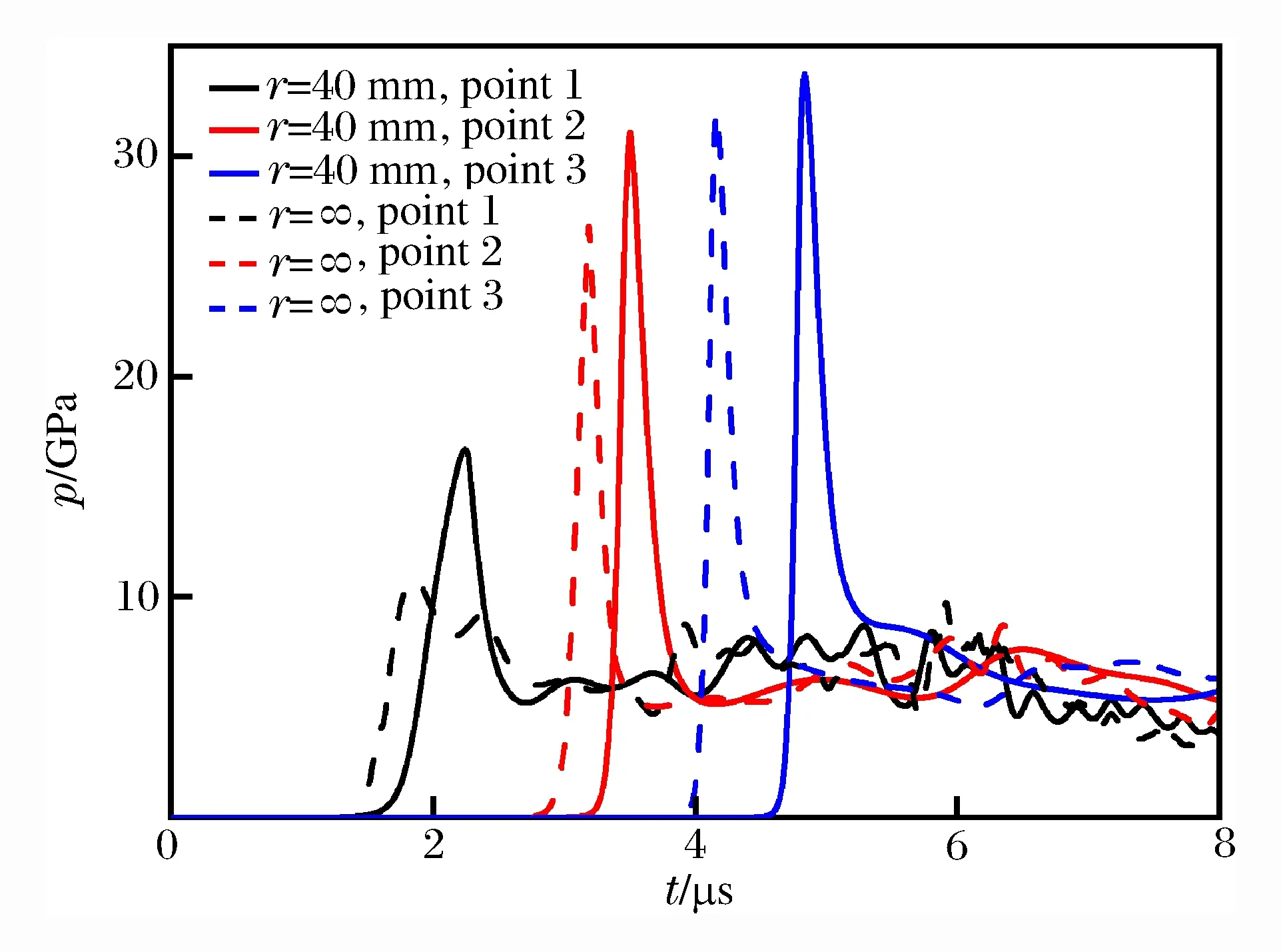
图4 柱壳和平面带壳装药内相同位置观测点压力时程曲线Fig.4 Histories of pressure at same point in cylindrical charge and plate charge

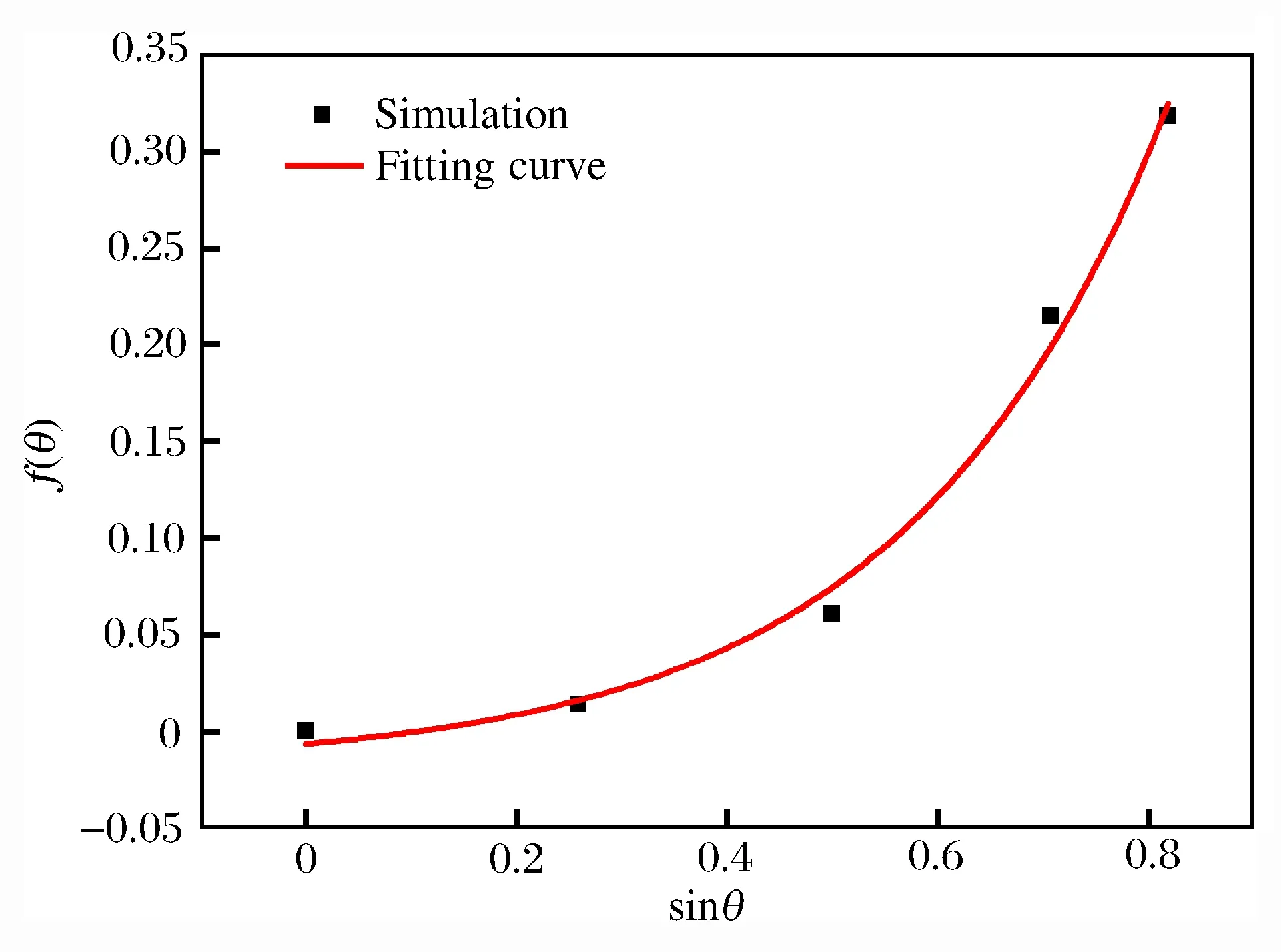
图5 f(θ)随入射角度正弦值的变化曲线Fig.5 Relation between f(θ) and sinθ

图6～7分别为不同入射角θ时的f(h/r)和其平均值随壳体厚度与装药曲率半径比值(h/r)的变化关系。由图7可以看出f(h/r)随h/r的增加而减小，但减小量在2%以内，说明曲率半径对柱壳装药的临界起爆速度有一定影响但影响不大。进一步得出f(h/r)随壳体厚度与装药曲率半径比值的变化关系，采用最小二乘法得到拟合公式为:

(14)

综上，得到考虑破片入射角和壳体形状系数的临界起爆速度修正因子的δ的计算公式(9)、(13)～(14)，将系数应用于式(5)，则得到基于Picatinny工程判据的临界起爆速度修正模型：

0<θ<55°， 0≤h/r<0.15

(15)

图6 f(h/r)随壳体厚度与曲率半径比值的变化关系Fig.6 Relation between f(h/r) and h/r

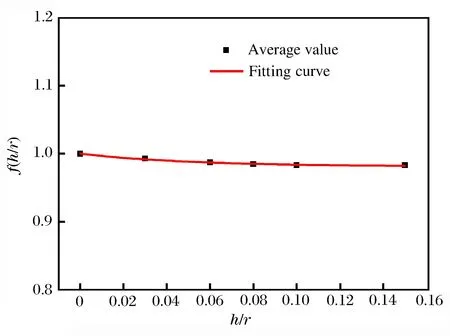
图7 f(h/r)平均值随壳体厚度与曲率半径比值变化关系Fig.7 Relation between average value of f(θ) and sinθ

4 判据校验

由于式(15)为特定破片质量条件下的装药临界起爆速度计算判据，为检验判据是否具有普适性，与文献已公布实验结果及部分计算数据进行对比。

首先将判据修正值与文献[14]公布的实验数据进行对比，质量为4.65 g破片撞击起爆平面带壳装药的实验值在2 231～2 522 m/s之间，修正判据计算的起爆阈值为2 347 m/s，修正判据计算值与实验数据吻合较好。

进一步开展不同质量破片撞击不同壳体厚度柱壳装药的数值模拟计算。表5为各工况下的临界起爆速度计算值及判据计算值。可以看出，计算值与判据修正值误差在7%以内，可认定修正的修正判据普适性良好。该判据同样适用于其他材质破片对柱壳装药的冲击起爆阈值的计算。

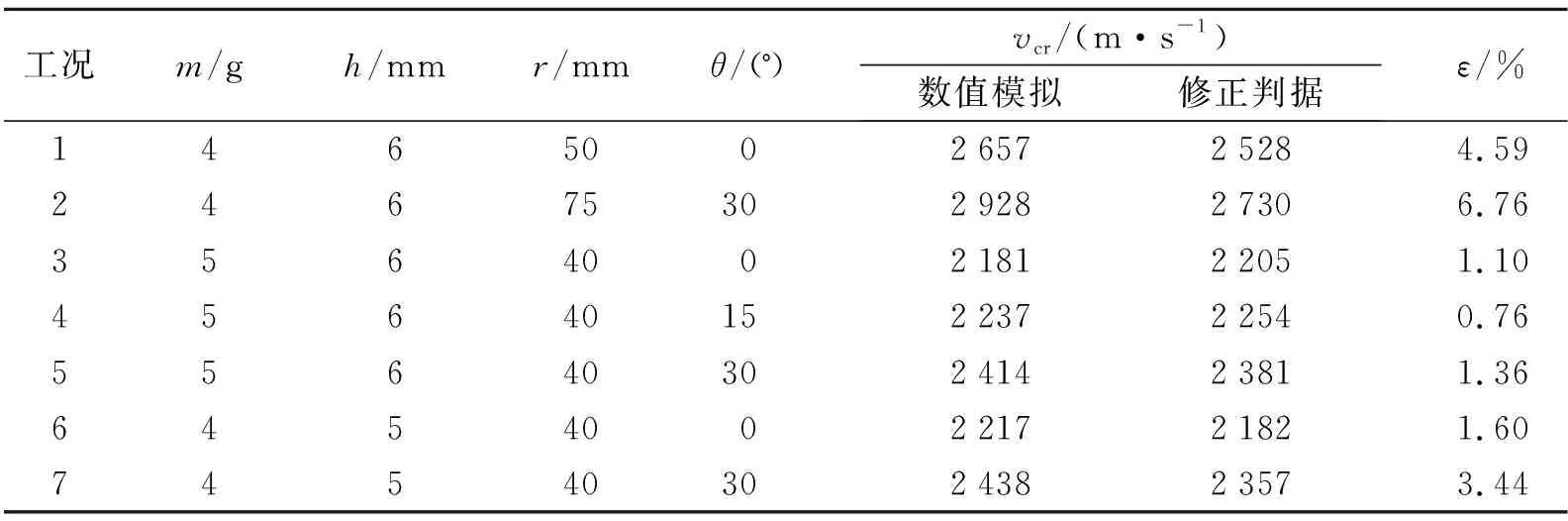
表5 不同质量破片临界起爆速度数值模拟与修正判据对比Table 5 Comparison of critical initiation velocities between simulation and rectified criterion value

5 结 论

采用数值模拟的方法，获得了破片以不同入射角起爆不同曲率半径柱壳装药的临界速度。通过对数值模拟结果的分析，建立了基于柱壳装药冲击起爆的修正判据，结论如下：

(1)入射角对柱壳装药冲击起爆影响较大，临界起爆速度随入射角的增大而非线性增加，装药曲率r=40 mm条件下，θ=55°时的起爆速度较θ=0°时增加35.6%；装药曲率对柱壳装药的冲击起爆有一定影响，临界起爆速度随曲率半径增加基本呈现非线性增大，入射角θ=0°条件下，r=∞时起爆速度较r=40 mm时提高3.2%。

(2)通过引入包含入射角θ和柱壳装药形状函数h/r的修正因子，对Picatinny工程判据进行修正，建立了适用于起爆柱面带壳装药临界破片速度的修正判据，判据校验表明修正判据与实验值与数值计算值误差小于7%，能较好的预测柱壳装药的冲击起爆。