数学模型在CT成像中的应用

徐旭华，雷 宇，黄旭东，廖平凯

（1.四川大学锦江学院数学学院,四川成都610207；2.四川大学锦江学院土木工程学院,四川成都610207）

一种典型的二维CT系统如图1所示，平行入射的X射线垂直于探测器平面，每个探测器单元看成一个接收点，且等距排列。X射线的发射器和探测器相对位置固定不变，整个发射-接收系统绕某固定的旋转中心逆时针旋转180次。对每一个X射线方向，在具有512个等距单元的探测器上测量经位置固定不动的二维待检测介质吸收衰减后的射线能量，并经过增益等处理后得到180组接收信息。现有均匀固体介质组成的标定模板，吸收率［1］具体数据见文献［2］，模板几何信息如图2所示。根据这一模板及其接收信息建立数学模型，确定探测器单元之间的距离以及该CT系统X射线的180个方向。

图1 CT系统示意图

图2 模板示意图（单位：mm）

1 模型分析与建立

为确定X射线的二维图像空间分布情况与椭圆固体介质的关系，根据模板示意图2，建立直角坐标系xoy，坐标原点为O，右边为X轴的正方向，上边为Y轴的正方向，X射线一次射入方向如图3所示，则根据简单的数学知识，可得到椭圆的方程

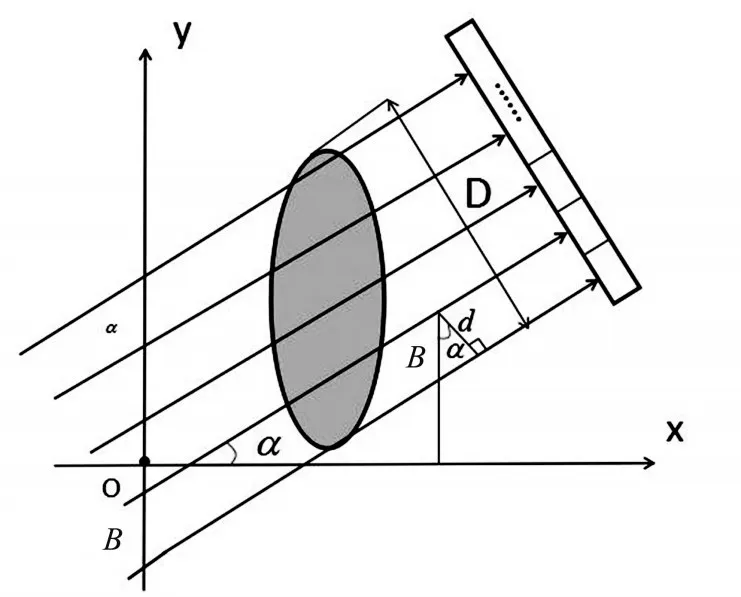
图3 X射线方向

为确定CT系统探测器单元之间的距离以及该CT系统使用的X射线的180个方向，文章首先依据面积优化模型得到对应的未知参数，再结合X射线的透射长度实际值与理论值建立优化模型。上述物体为均匀介质，查阅文献［3］可知CT所用的X射线与物质之间相互作用的衰减规律可用以下定律描述：

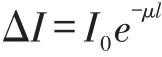
其中l为物体中的透射长度；μ为物体对X射线的衰减系数；I0是入射物体前的X射线强度；ΔI是射线强度的入射物体后的衰减量。结合X射线与检测器之间的对应关系，可得到检测器吸收到的强度I为：

根据上式即可求得实际透射长度l的表达式为：

根据极限的思想，当n→+∞时，第n-1条射线与第n条射线及椭圆所围成的面积可以近似成一个小矩形的面积，记成Sn-1=ln-1d，其中ln-1是第n-1条X射线透射长度，d是探测器单元之间的距离，整个椭圆可以近似看成是n-1个矩形构成，由简单的数学知识可知椭圆的面积为πab，其中a、b分别为椭圆的长半轴、短半轴的长。设lik是第i次旋转方向上第k条射线所透射的实际长度，那么可以得到X射线一个入射角度的优化模型：

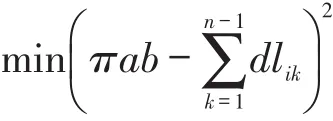
整个发射-接收系统绕某固定的旋转中心逆时针旋转180次，从而有180个射入角度上的优化模型：

面积优化模型

根据图3可以得到X射线与椭圆固体介质相切的第一条直线的方程式为y1=xtanα+L，然后可得到任意两条X射线在y轴上的截距之差B与探测器单元之间的距离d之间的关系式为：

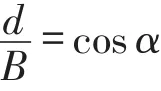
显然X射线的方程为：

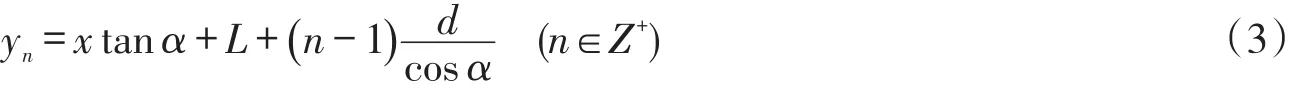
设Am(xm,ym)(m=1,2...n-1)，Bj(xj,yj)(j=1,2...n-1)是椭圆介质与 X射线的两交点，联立（1）式与（3）式可求出Am，Bj之间的距离为：

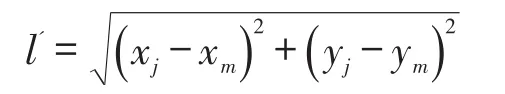
根据以上分析，l′可以看成是射线透射介质中的理论长度，考虑到射线透射介质中的实际长度可以由（2）式求出，设是第i次旋转方向上第k条射线所透射的理论长度，可建立射线透射的理论长度与实际长度的优化模型：

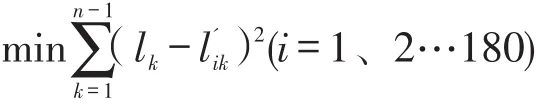
整个发射-接收系统绕某固定的旋转中心逆时针旋转180次，从而有180个角度上的优化模型：

长度优化模型

2 模型求解

对于探测器单元之间的距离及X射线的180个方向的求解问题可采用最小二乘法［4］加以解决，利用Matlble数学软件进行编程求解［5］。首先采用椭圆面积优化模型求解得到部分参数，其次结合透射长度的理论值与实际值的优化模型对剩余参数进行求解，求解步骤如下：

Step1：将接收信息数据［2］带入式（2），可求解得到透射长度；

Step2：近似将X射线与椭圆所围成的图形看成是n-1个矩形，则用实际透射长度值lik乘以探测器单元之间的距离d，得到其中一个矩形的面积，记成likd；

Step3：将面积likd代入到椭圆面积优化模型中，根据接收信息数据［2］可得到一组最优化的参数d、I、μ；

Step4：将求解得到的优化参数代入长度优化模型中，原有五个参数d、I、μ、α、L减少至两个参数α、L，根据接收信息数据［2］，可以得到参数α、L的最优解。

根据上述步骤求解得到探测器单元之间的距离d=0.2810mm，CT系统使用的X射线的180个方向如表1所示。

表1 模型测量方向

3 方差、回归及残差分析

该问题的实际数据如表2所示。

表2 实际方向

根据上述模型计算出的结论前10个方向上和实际数据是有所差异的，但从第11个方向开始，理论模型的数据就和实际数据很接近了，从第11方向开始用SPSS软件对实际数据和理论数据进行方差分析。

表3 单因素方差分析

从表3可以看出P=0.998955＞0.05，可以认为从第11个方向开始上述模型算出的方向角和实际方向角没有显著差异。通过SPSS软件，容易求得R2=0.999977431，说明在置信度为95%的条件下，上述模型对数据的解释总体令人满意，如表4、5所示。

表4 回归统计

表5 方差分析

如表6所示，设实际方向角为因变量y，模型计算结果为自变量x，由上述回归分析可得出其一般回归方程为：

表6 回归分析

同理，可以利用SPSS软件进行残差分析，如表7及图4所示。

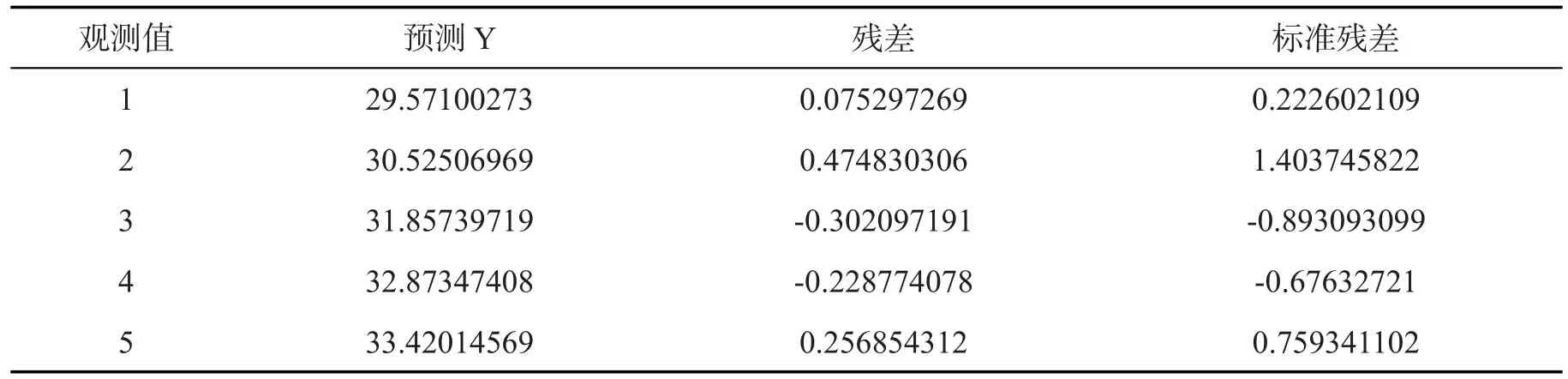
表7 残差输出

观测值 预测Y 残差 标准残差6 7 8 9 1 0 11 34.49242522 35.44649218 45.09316926 118.1362328 207.4039468 208.5189443 0.15387478 0.199807816-0.296469262-0.692532849 0.242353187 0.116855708 0.45490163 0.590693947-0.876455194-2.047342138 0.716471274 0.345461757

图4 残差图

从图4可以看出残差没有完全落在一条水平带之间，说明模型是有误差的，但总体来说，模型的结果是可以接受的。

4 总结

文章试图利用数学模型解决现实生活中的问题，在面积优化模型建立的过程中，假设X射线将椭圆无限分割成可数个矩形，但实际上CT探测器上只有512个接收点，除去和椭圆相切的两条，X射线最多将椭圆分割成511个小区域，并且这些有限的小区域并不能保证是矩形，这给后来的运算带来误差。在对模型结果与实际数据分析中，是从第11个方向开始进行方差分析，而忽略了前10个方向，这都无疑会直接影响到模型的真实性与实用性，但该模型在一定程度上说明了X射线的大致方向，在解决实际生活中的优化问题时有一定借鉴意义。