电选粉煤灰颗粒图像识别与烧失量预测模型

陈师杰 ，李海生 ，1b，陈英华 ，1b，温晓龙 ，章新喜 ，1b，孙 猛 ，陈 明

（1.中国矿业大学 a.化工学院；b.煤炭加工与高效洁净利用教育部重点实验室，江苏徐州 221116；2.中国平煤神马集团一矿，河南平顶山 467000）

煤炭资源是目前世界上最主要的能源之一，我国煤炭利用率占能源总量的一半以上。粉煤灰是一种因煤炭燃烧不完全而产生的污染物，大量未经处理就直接排放的粉煤灰对大气环境造成了严重的污染。

粉煤灰中未燃尽炭粒的含量高，吸水性大，强度低，将不利于粉煤灰的资源化利用[1]，因此，需要进行脱炭处理。粉煤灰的脱炭技术主要有湿选法和干选法，电选脱炭技术是干选法的典型方法之一，主要用于缺水地区，不会对环境造成二次污染，是一种物理方法，且不污染粉煤灰产品，设备简单，投资较小，效率高。

烧失量是表征粉煤灰中未燃烧完全有机物的重要指标。为了实现粉煤灰的重复利用以及评估煤炭的燃烧效率，需要对粉煤灰的烧失量进行检测[2]。传统的检测法需要人工取样、灼烧和称重。检测需要的时间周期较长，无法实现全天连续实时检测。

本文中运用图像特征信息快速分析法和极限学习机神经网络，探索由图像特征信息识别电选粉煤灰烧失量的可行性，为粉煤灰烧失量的快速在线检测提供了一种新的方法。

1 实验

1.1 材料

为了配置多组烧失量各不相同的粉煤灰样品，分别在不同地区的电厂采集原始的粉煤灰样品，其烧失量分别6%和35%。通过质量配比的方式，获得40组不同烧失量梯度的粉煤灰样品。使用粉碎机将配置好的粉煤灰粉碎为粒径小于75 μm的粉尘颗粒，统一放在马弗炉中脱除水分并保温24 h以上备用。

1.2 实验系统

由于光照对图像的特征参数有较大的影响，因此要通过图像特征参数准确预测粉煤灰的烧失量，要求实验在稳定的光照环境下进行。图像的获取选择在一个暗室中进行，暗室内部有固定的光源，通过计算机控制工业摄像头对不同烧失量的粉煤灰进行拍摄，从而获得不同梯度烧失量粉煤灰的样品图片。

1.3 图像的获取

将配比得到的40个不同的粉煤灰样品根据烧失量的大小依次放入暗室中进行拍摄，暗室内的光源选择固定的白光，光照强度为400 lux，每个样品连续拍摄5组图片，选择图片效果最佳的一组作为该样品所对应的图片。如图1所示为在同一光源的暗室内不同烧失量的粉煤灰样品的样张。

由图1可知，烧失量大小不同的粉煤灰存在视角上的明显差异，烧失量越大，图像越暗，其对应的图像特征参数也会存在差异[3]。通过MATLAB软件对图像进行处理来识别这些差异，就可以获得与其对应的烧失量[4-5]。

图1 不同烧失量粉煤灰样品的样张Fig.1 Samples of different LOI of fly ash

2 图像的特征提取

通过工业相机拍摄到的图片为最常见的RGB图片，为了获得图像的灰度特征参数需要先将图片灰度化，将RGB图像转换为灰度图像。一般灰度图像的灰度级从0～255，总共256种取值，每个颜色深度代表一个灰度级。一般通过灰度直方图来描述一幅图像的灰度级，灰度直方图的定义[6]为

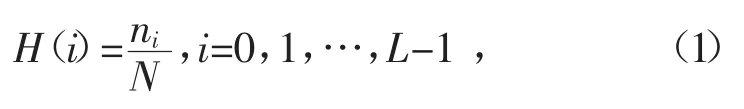
式中：N表示灰度图像的像素点总个数；ni表示某个灰度级i的像素点数量。对于灰度直方图而言，其横坐标代表灰度级，纵坐标代表该灰度出现的频率。

图2 所示为烧失量为7.84%的粉煤灰样品图像归一化后的灰度直方图。可以看出，由于粉煤灰内部成分对光照反射的差异，导致灰度图像灰度分布区域不同。以烧失量为7.84%的粉煤灰为例，灰度级分布范围在100～200，灰度级在150～180的像素点所占比例较大，超过整张图的50%，通过灰度直方图可以估计图像的灰度平均均值为150～180。

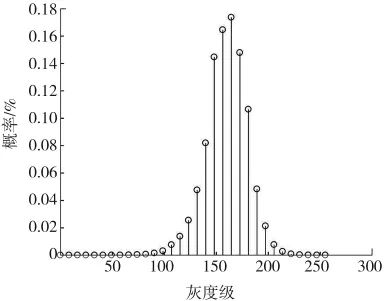
图2 粉煤灰归一化灰度直方图Fig.2 Fly ash normalized histogram

图像的灰度均值是反应整个灰度图像纹理平均亮度的度量。粉煤灰烧失量越高，光照的反射也会变得越弱，图片也会显得越暗，图像的灰度均值也会越低。对于一幅归一化后的灰度直方图，图像灰度均值表示为

图像的灰度方差反映了灰度图像的灰度数值的离散程度，图像的标准方差是图像纹理平均对比度的量度。在粉煤灰的烧失量检测中，灰度图像的方差也具有一定的数据意义。图像各个像素点的灰度方差可表示为

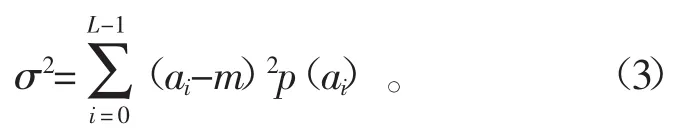
图像的能量反映了灰度图像灰度值的均匀程度，通常情况下，图像的灰度值分布越均匀，图像的能量越大；反之，图像的能量便会越小。图像能量在粉煤灰烧失量检测中能够反映粉煤灰的碳与灰的分布均匀情况以及样品混合的均匀程度。图像能量表示为

图像的熵值反映了灰度直方图分布的均匀性，熵值越大表明图像的随机性也越大；反之，图像的随机性越小。这里给图像的熵值定义为

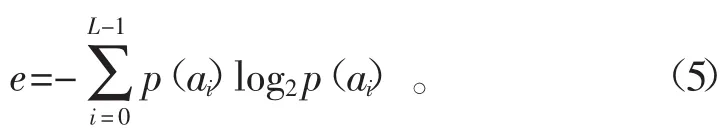
根据上述公式，通过使用MATLAB软件对图像进行处理，借助MATLAB强大的数值分析能力和运算能力，可以分别对不同烧失量的粉煤灰的各个参数进行提取和分析，由此可以获得不同烧失量的粉煤灰的图像灰度均值、图像灰度方差、图像灰度熵值以及图像能量的关系图，如图3—6所示。

通过分析发现，随着粉煤灰烧失量的增加，图像逐渐变暗，灰度图像的灰度均值有明显减小的趋势。粉煤灰的烧失量大小与其他3个特征参数的关系比较微妙，通过单个特征量与输出量进行拟合来进行预测往往不能达到精度要求。本研究中，运用极限学习机将多个图像特征参数同时作为输入来对粉煤灰的烧失量进行回归预测，实现对粉煤灰烧失量的准确预测。

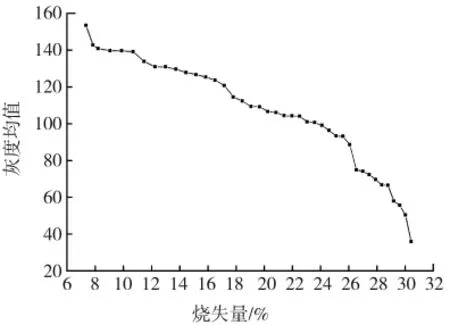
图3 灰度均值与粉煤灰烧失量关系图Fig.3 Relationship between average gray value and LOI of fly ash

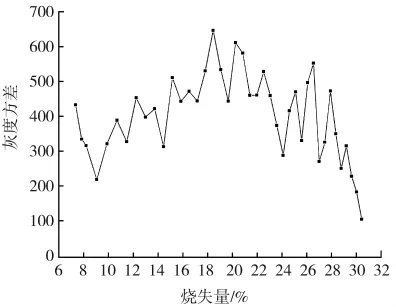
图4 灰度方差与粉煤灰烧失量关系图Fig.4 Relationship between gray variance and LOI of fly ash

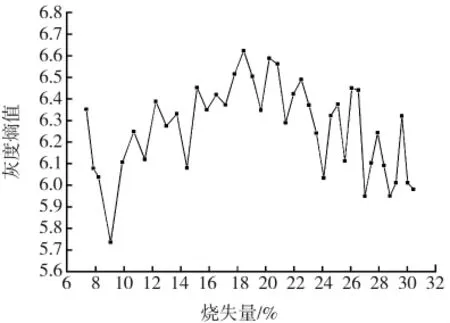
图5 灰度熵值与粉煤灰烧失量关系图Fig.5 Relationship between gray entropy and LOI of fly ash

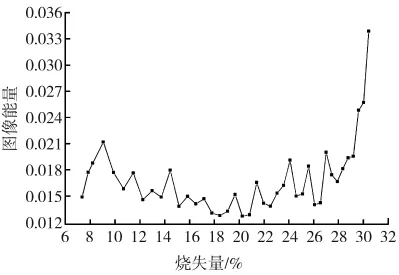
图6 图像能量与粉煤灰烧失量关系图Fig.6 Relationship between image energy and LOI of fly ash

3 极限学习机建模

极限学习机是一种针对前馈神经网络的新型算法[8]。该算法随机产生输入层与隐含层之间的连接权值和隐含层内的阈值，在训练过程中，不需进行调整且能快速找到唯一最优解[9]。极限学习机网络结构图如图7所示。

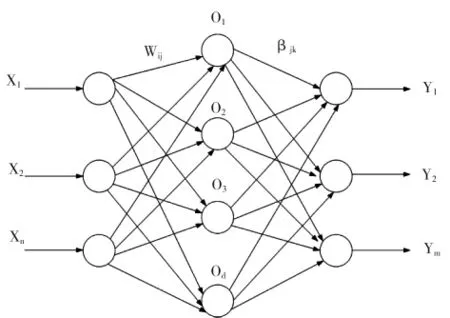
图7 极限学习机网络结构图Fig.7 Extreme Learning Machine Network Structure

由图7可得，若设输入层与隐含层的连接权值[10]为

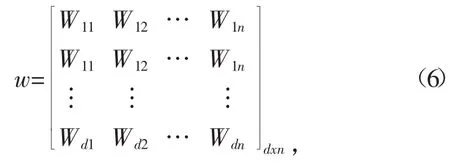
设隐含层与输出层的连接权值

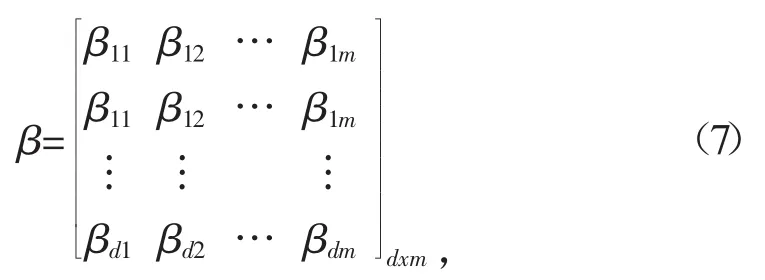
可得当输入样本集为Q时，设隐含层神经元的个数为d，隐含层神经元的阈值为

若设神经网络的激活函数为g（x），极限学习机神经网络的输出为

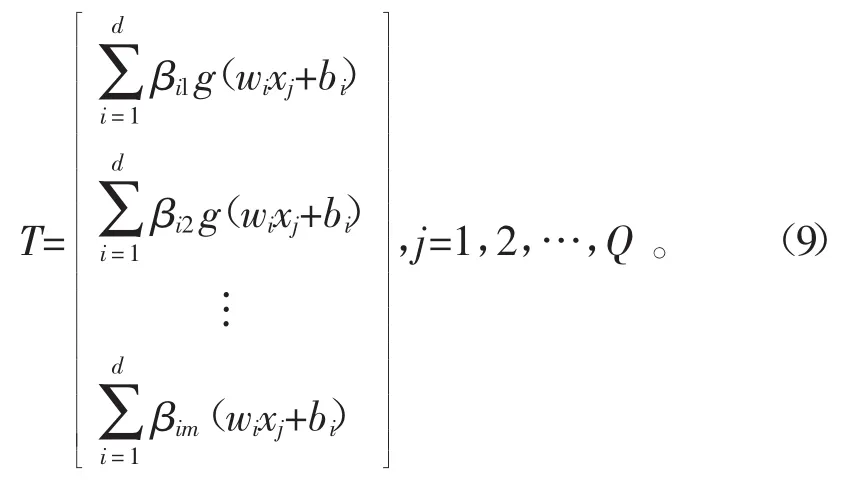
由黄广斌等[11，12]人提出的关于极限学习机的两大定理，可得当极限学习机的样本个数与隐含神经元个数相等时，对于任意的权值w和阀值b而言，测试集都可以零误差逼近样本值。通常情况下，为减少计算量，隐含神经元的个数取值要小于训练样本的个数[13-14]。

4 极限学习机模型训练与预测

要利用极限学习机对粉煤灰的烧失量进行训练与预测，需要将极限学习机的基本算法程序输入MATLAB中，通过MATLAB来进行运算建立模型，极限学习机实施的主要步骤如下：

1）将100组精选后粉煤灰灰度图像所对应的灰度均值、灰度方差、图像熵值和图像能量组成的向量作为输入样本，粉煤灰的烧失量作为输出。极限学习机的训练样本为100组，测试样本为5组。

2）取隐含层节点初值L=10，逐步增加获得ELM隐含层最佳节点的个数。

3）选择最佳的g（x）激活函数，通过比较3种激活函数的神经网络均方误差，选择合适的激活函数[15]。

由于ELM在建立模型的过程中，隐含层节点的选择对实验预测的结果影响很大[16]，因此首先应该先确定隐含层节点的个数，取隐含层节点初值为10，逐步增加，并计算对应的神经网络的均方误差作为参考，不同隐含层节点所对应的均方误差如表1所示。

表1 不同隐含层节点所对应的均方误差Tab.1 Mean square error corresponding to different hidden layer nodes

由表1可以看出，随着隐含层节点的逐步增加，极限学习机的均方误差MSE也逐渐减小，ELM的学习能力就越强，隐含层节点的个数增加到一定值时，所对应的MSE就趋于一个稳定的值。为了对粉煤灰的烧失量进行较为精准的预测，选择隐含层神经元节点数为25。

在神经元节点数为25的前提条件下，需要选择一个误差最小的激活函数g（x）。

选择最常见的3种激活函数sig函数、sin函数和hardlim函数分别进行比较分析，3种函数对同一测试样本组的神经网络均方误差（σMSE×10-4）如表2所示。

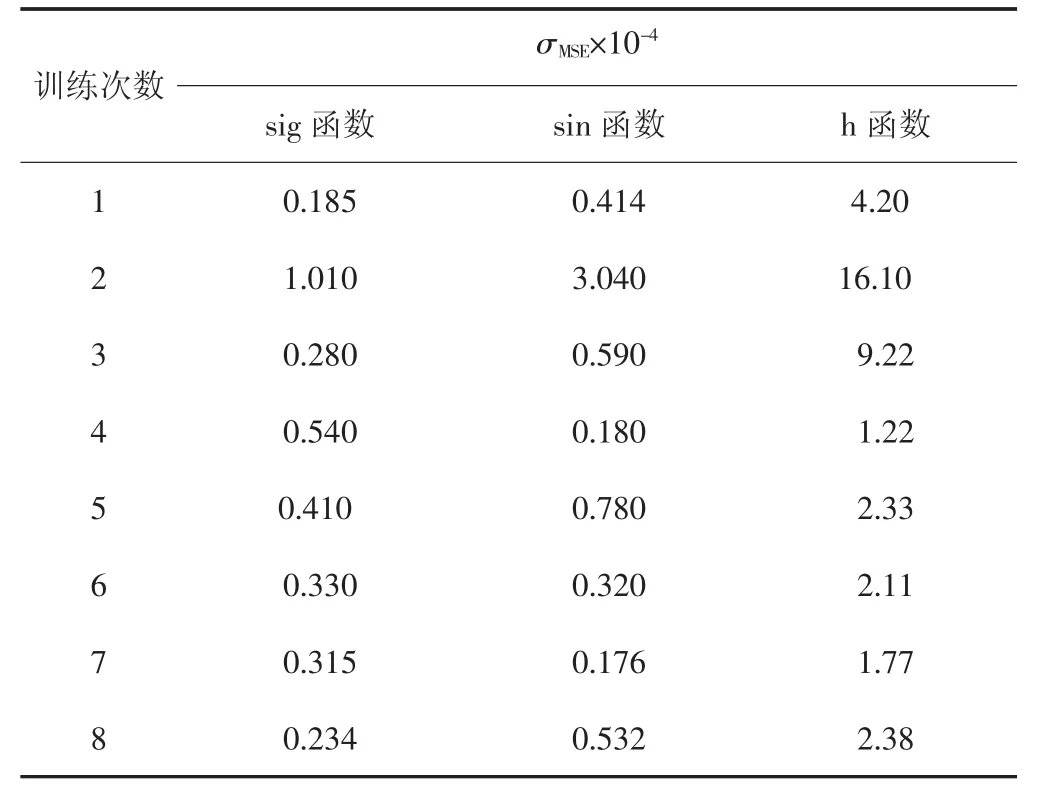
表2 3种激活函数预测样本对应的均方误差Tab.2 Mean square error of three activation functions

由表2可知，通过极限学习机来对同一粉煤灰的测试样本进行多次训练，可以得到当激活函数为sig函数时，神经网络的平均均方误差为4.013×10-5；当激活函数为sin函数时，神经网络的平均均方误差为7.54×10-5；当激活函数为hardlim函数时，神经网络的平均均方误差为49.16×10-5，因此通过比较3种函数的预测效果，可知在相同的隐含层节点条件下对同一样本的烧失量进行预测，sig函数的预测效果比其它两种激活函数的预测效果要好。

5 应用与评价

配置10组与训练样本集烧失量完全不同的粉煤灰样品，通过MATLAB软件提取出10组样品的特征参数，将10组样品的特征参数作为神经网络的输入，使用极限学习机对10组样品的烧失量进行预测。选择sig函数作为神经网络激活函数，隐含层的节点个数为25，分别获得10组样品预测烧失量。把10组样本分别放入马弗炉中加热灼烧，获得粉煤灰的实际烧失量，将10组样品的预测值与实际值进行对比，结果如图8、9所示。

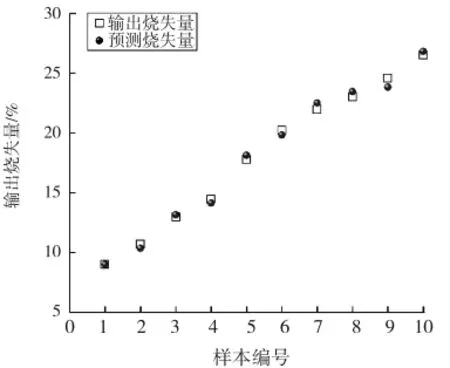
图8 粉煤灰样品烧失量的预测值与实际值对比图Fig.8 Prediction and actual of fly ash LOI

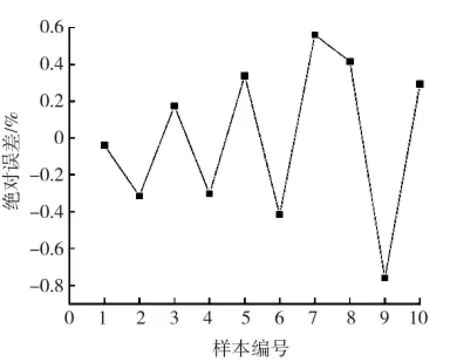
图9 粉煤灰烧失量预测值的绝对误差Fig.9 Absolute error of predictive value of fly ash LOI

通过图8、9可以得出，极限学习机对粉煤灰的烧失量进行预测，预测样品的最大绝对误差都低于1.5%，说明极限学习机在对粉煤灰烧失量的预测效果极好，对多个样品进行多次预测，并比较预测值与真实值的大小，如表3所示。

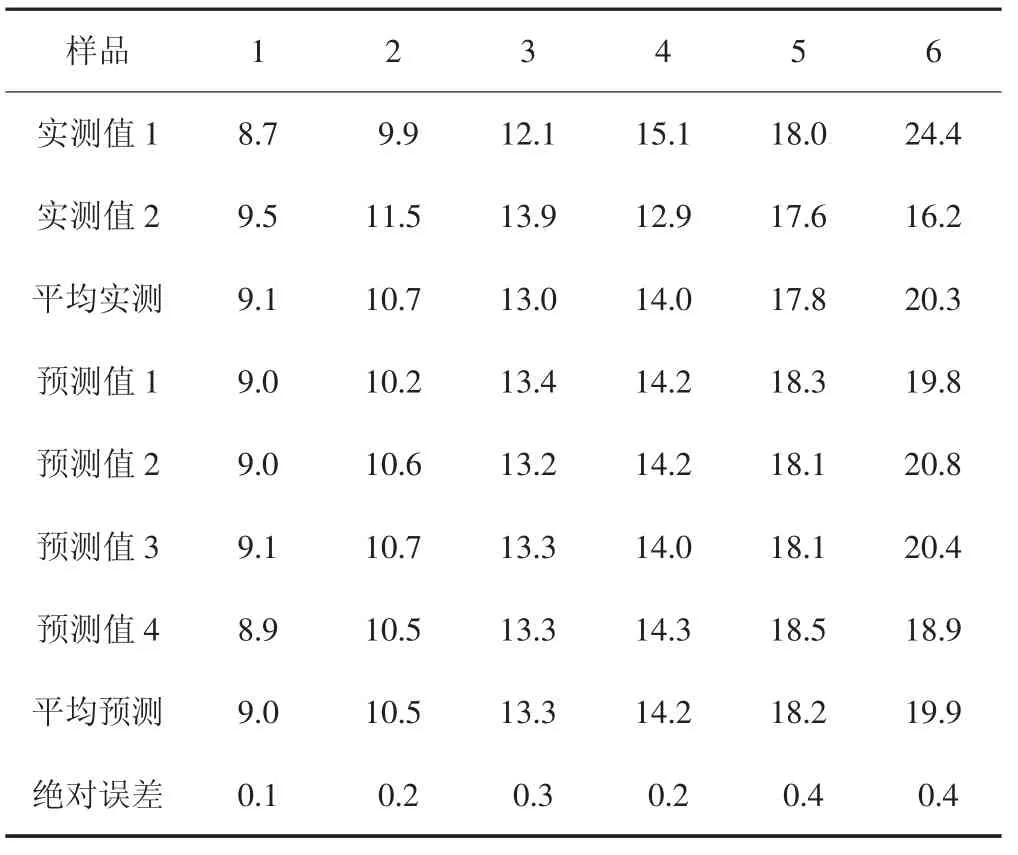
表3 电选粉煤灰烧失量的实测值与预测值比较结果Tab.3 Comparison of the measured and predicted values of the LOI of fly ash

6 结论

1）应用极限学习机构建了粉煤灰烧失量预测模型以及粉煤灰图像识别系统的技术方案，能够快速准确地对粉煤灰的烧失量进行预测，方案切实可行，准确度高，为工业生产中电选粉煤灰烧失量的快速在线检测提供了技术参考。

2）通过对比电选粉煤灰烧失量的实测值与图像预测值，表明极限学习机神经网络模型符合粉煤灰烧失量在线预测的技术要求，该模型应用sig激活函数，选择合适的节点数，可以实现最佳预测效果，达到高精度预测要求，并能够准确反映电选粉煤灰烧失量与不同组分图像特征的数学模型，可以用于工程技术应用。