随机跳风险与随机强度组合模型的欧式期权定价

2019-01-02

金融经济 2018年22期

一、引言

自从由Black和Scholes[1]提出期权定价理论，该理论在股票价格变化分析方面得到了有效应用。针对扩散模型，需假设价格连续变化。伴随着后续研究的不断深入，人们发现在实践运用过程中，Black-Scholes模型分析结果与实际情况存在出入。一旦有重大事件发生，如认识变动、灾难等，会有重大信息出现。此时，股票市场上将出现价格大幅度波动，呈现出跳跃性的特点。出现这种情况，主要是由于以往模型采用的是纯粹的假设因素。针对这一问题，后续学者不断进行模型改进，以便使Black-Scholes 模型得到更好的推广运用。从实践研究来看，在股票市场上，不连续波动的发生，主要是受到了利率跳变的影响[2-6]。

本文通过分析股票市场结构，联合分析随机跳风险与随机强度，并提出了相应的组合模型。在此基础上，通过对以往的傅里叶反变化、Feynman-Kac公式等进行联合运用，则能更好的完成欧式期权定价分析。从模型特点上来看，跳风险的引进，同时加强市场利率跳变，使得股票波动与随机变化相关性更加显著，因此得到的结果更具普遍性。

二、市场模型

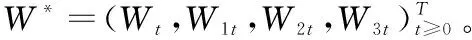
因为Poisson跳过程存在，同时存在V1,V2这两个无法交易因素，因此市场不完全。受这一因素影响，尽管存在等价鞅测度，却不止一个。为加强风险中性定价，还要采用最小熵测度等.假设Q为特选测度，可以得到短期利率r(t)满足

r(t)=V1(t)+V2(t)，

(1)

其中

(2)

Λ指的是股票跳跃强度，满足式(3)

(3)

以及股价S无连续红利支付并满足

(4)

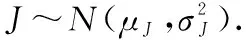
三、主要结果及证明

首先，T为到期日，可知无风险债券价格能够利用引理1推导.

引理1 (1)、(2)为利率模型，对无风险债券进行分析可得

P(t,T)=P(t,V1,V2,T)=exp(A(t,T)-B(t,T)V1-B1(t,T)V2)，

其中

(5)

(6)

(7)

b2=r2-a2,a3=2+μ1r1+μ1a1,b3=μ1r1-2-μ1a1,a4=-2+μ2r2+μ2a2,

b4=μ2r2+2-μ2a2.证明：根据Feynman-Kac公式得出P(t,V1,V2,T)满足下列P.D.E：

(8)

以及P(t,V1,V2,T)=1

由于模型(1)，(2)均是仿射结构的，于是T期无风险债券P(t,T)有指数形式的解：

P(t,T)=P(t,V1,V2,T)=exp(A(t,T)-B(t,T)V1-B1(t,T)V2)

(9)

将(9)代入(8)，得：

(10)

且

A(T,T)=0,B(T,T)=0,B(T,T)=0.

化简得

(11)

比较V1,V2前面的系数可以得出下列O.D.E：

求解(12)、(13)得B(t,T)、B1(t,T)代入(14)式，能够得到A(t,T).

通过推导，可知无风险债券价格P(t,T)应该达到S.D.E.

在欧式期权定价分析时，需要先确定看涨期权.

根据无套利原理，条件为T，K为执行价，可以得到t时看涨期权价

(15)

IA为示性函数.

在对条件期权进行计算时，需要完成新概率测度Q1、Q2的定义，以S(t)为计价单位，实现测度Q1的变换，以P(t,T)为计价单位，完成测度Q2变换：

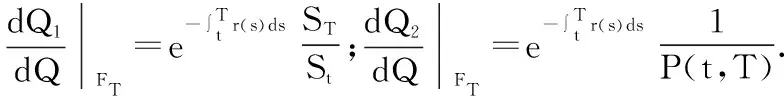
(16)

由Q1、Q2为概率测度且等价于Q，则

VC(t,S;V1,V2)=StQ1(ST>K)-KP(t,T)Q2(ST>K)

=StQ1(lnST>lnK)-KP(t,T)Q2(lnST>lnK)

(17)

为了得到概率Q1、Q2闭式解，需要导出其相应的特征函数式，定义

(18)

则

(19)

以及

(20)

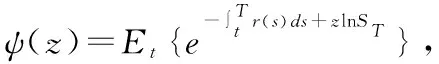
从而

(21)

(22)

定理1 在(1)，(2)，(3)，(4)模型应用基础上，在T时刻，执行K，可得欧式股票看涨期权价格：

(23)

证明：由Fourier反变换和分布函数的关系知

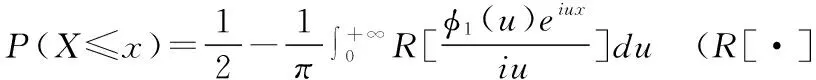
(24)

从而

(25)

(26)

将(25)、(26)代入(17)中，得证定理.

推论1 在金融市场模型(1)，(2)，(3)，(4)下，T时刻，执行K，可得欧式股票看跌期权价：

（3）树立危机意识。危机意识是企业财务管理人员必须时刻具备的，正所谓“生于忧患”，企业财务管理人员在新时期更需要重视自身理论观念的充实、丰富与发展，培养接纳新事物，勇于挑战的心理素质，要充分意识到经济开放性所带来的机遇与挑战，梳理企业发展面临的困难，树立危机管理意识，积极向外开拓新的业务与对外合资渠道，全方位、多层面的促进企业资本的多元化发展，将“鸡蛋”放在尽可能多的“篮子”里，降低企业财务风险。

(27)

从(23)式可看出，期权价格的计算依赖于特征函数φ1(u)、φ2(u)的表达式，而有(21)、(22)式，故只需计算ψ(z)的表达式如下：

(28)

于是

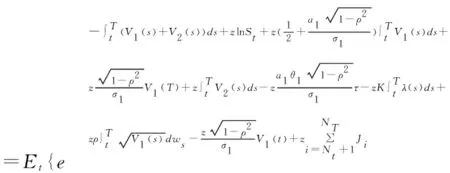
(29)

其中

在(29)式中，

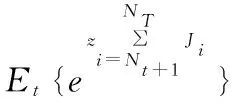
(30)

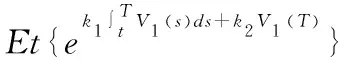
(31)

其中

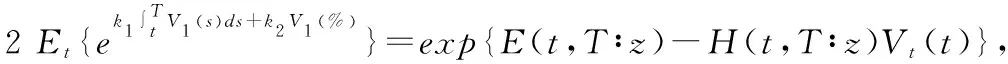
(32)

(33)

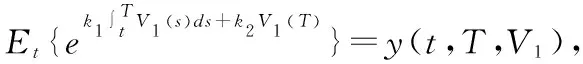
则由Feyman—Kac定理可知，知y(t,T,V1)是下面向后PDE方程的解

由于v1满足仿射结构形式，故y(t,T,V1)有指数形式的解，设y(t,T,V1)=exp{E(t,T∶z)-H(t,T∶z)V1(t)}，将其代入上述PDE方程并求解即可得证。

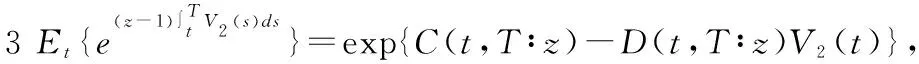
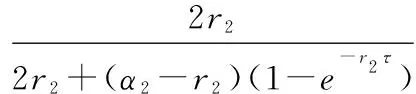
(34)

(35)

证明：证明过程类似引理1。

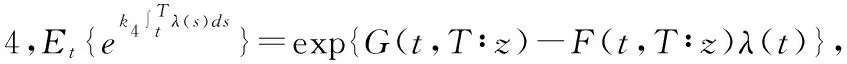
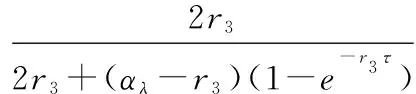
(36)

(37)

证明：证明过程类似引理1。

综合上述引理2—4，得

ψ(z)=exp{E(t,T∶z)-H(t,T∶z)V1(t)}·exp{C(t,T∶z)-D(t,T∶z)V2(t)}·exp{G(t,T∶z)-F(t,T∶z)λ*(t)}·ezk3=exp{E(t,T∶z)-H(t,T∶z)V1(t)+C(t,T∶z)-D(t,T∶z)V2(t)+G(t,T∶z)-F(t,T∶z)λ(t)-zk3}

(38)

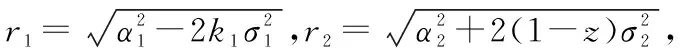
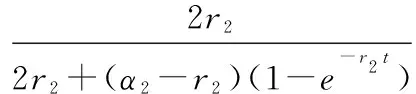
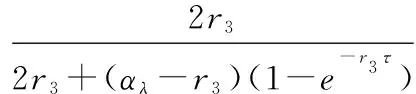
于是有

引理5 定理1中的两个特征函数、φ2(u)的表达式分别为：

φ1(u)=exp{(E(t,T∶1+iu)-E(t,T∶1))-(H(t,T∶1+iu)-H(t,T∶1))V1(t)+(C(t,T∶1+iu)-C(t,T∶1))-(D(t,T∶1+iu)-D(t,T∶1))V2(t)+(G(t,T∶1+iu)-G(t,T∶1))-(F(t,T∶1+iu)-F(t,T∶1))λ(t)+iuk3},

(39)

φ2(u)=exp{(E(t,T∶iu)-E(t,T∶0))-(H(t,T∶iu)-H(t,T∶0))V1(t)+(C(t,T∶iu)-C(t,T∶0))-(D(t,T∶iu)-D(t,T∶0))V2(t)+(G(t,T∶iu)-G(t,T∶0))-(F(t,T∶iu)-F(t,T∶0))λ(t)+iuk3}.

(40)