混合多处理机任务作业车间调度问题的仿真研究
2018-12-29
(北京林业大学 经济管理学院,北京 100083)
0 引言
制造车间调度是排序问题研究体系的一个重要组成部分,它关系到企业整个生产系统的正常运转,关系到制造企业的成本和利润,一直以来都是学者们研究的热点问题。其中,钢结构件制造车间,因其加工工艺的特殊性,使车间调度系统比典型的作业车间调度(Jobshop Scheduling Problem,JSP)更为复杂。其作业以组对、焊接为主,基本流程为:下料→组对→焊接→修整,每道工序都需多位技工共同加工完成。不同于传统车间调度要求每个工件的每道工序只需在一台处理器上加工,钢结构件制造车间需要多个处理机(机器或人)同时进行加工,使得这类生产车间目前还主要根据调度人员的经验来排产,严重企业影响生产效率。
从上世纪90年代末开始出现了专门针对车间调度中的多处理机任务问题(Multiprocessor Task Scheduling,MTS)的研究[1]。研究初期还是主要集中于针对只有一道加工工序的工件的MTS问题,Drozdowski[2]根据机器有无差异对MTS问题从无差异的并行机和有差异的专用机这两方面进行了详尽的综述。
进入21世纪后,逐渐出现了一些针对工件具有多道加工工序的多处理机任务调度方面的研究,并逐渐成为研究者关注的热点,其中流水车间涉及的比较多(可看作是JSP问题的特例)。但由于作业车间相对于流水车间来说更加复杂,有关具有多处理机任务约束的混合作业车间调度(Hybrid Job-Shop Scheduling with Multiprocessor Task, HJSMT)问题的研究成果仍然很少。Brucker & Kramer[1]证明了即使只有两台处理机的HJSMT问题也为NP-hard难题。Huang 等[3]针对四台处理机只考虑一道加工工序,即HJSMT的简化MTS问题,提出一种线性时间内的近似算法。Gröflin等[4]对具有工件插入的多处理机任务作业车间调度进行了研究,但该研究是基于已有可行的调度策略的假设,只对插入策略进行研究,并没有实现对于HJSMT的调度方案设计。
随着制造业市场的不断发展,为提高生产效率,越来越多的企业对复杂工序采取多台处理机同时加工以减少生产时间提高生产效率的生产方式,但是目前对于这种具有多处理机任务约束的混合作业车间调度的研究较少,而这类问题也确实广泛存在于钢结构制造企业的生产过程中。因此本文主要针对具有多处理机任务约束的混合作业车间调度建立仿真模型,并根据运用遗传算法进行优化求解,以获得更有效率的生产调度方案。
1 HJSMT调度问题建模
不同于JSP问题每道工序只需一台处理机进行加工操作,HJSMT问题每道工序都需要不少于一台处理机同时进行加工操作,即相当于对JSP问题增加了MTS问题的约束,故对于HJSMT问题的一般性描述如下:有n个工件通过m台处理机进行制作,每个工件都需多道工序,同一工件的各工序间存在先后顺序,且必须按照该顺序生产(工艺路线约束)。每道工序都需不少于一台处理机同时进行加工操作,每台处理机同一时刻也只能进行一项加工工作(有限资源约束)。目标是找到一种调度方案,将所有工序在满足工艺路线和有限资源约束的前提下,分派到各处理机上处理加工,并且总加工时间Cmax最小。
对于HJSMT模型有以下假设:
1)所有处理机在开始时都是可用的;
2)订单情况已知,包括处理机数、工件数以及工件的加工工序和时间;
3)每道工序同一时刻需要不少于一台处理机同时加工;
4)下一工序必须在上一工序完成后进行;
5)每台处理机同一时刻只能对一个工件进行处理;
6)处理机加工过程不可打断,不可插入其他工件。
为了便于问题的讨论和描述,对于HJSMT问题的相关符号和参数进行定义:
N:工件数量;
m:处理机数量;
Ji:工件i,i = 1, 2, ..., n;
|Ji|:工件i所包含的加工工序的数量;
Mk:处理机k,k=1,2,...,m;
tij:工件i的第j道工序的加工时间;
eij:工件i的第j道工序的完工时间;
Cmax:完成所有工件加工的最大完工时间。
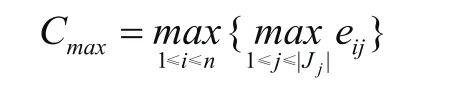
根据优化目标,建立数学规划模型:
目标函数:

约束条件:
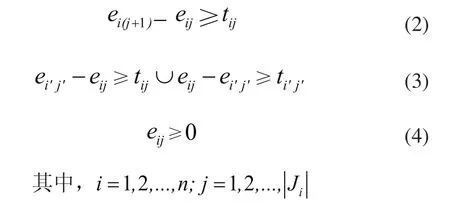
其中,式(2)表示工艺约束,第j+1道工序必须在第j道工序结束后进行,保证各工件可以按照既定的加工先后顺序进行加工;式(3)表示机器约束,确保每台处理机在同一时刻只能对一个工件进行加工,并且安排了各工件在同一处理机上的加工顺序。
2 遗传算法优化
1975年,Holland J H通过模拟生物进化的机制,提出了遗传算法(Genetic Algorithm,GA)框架[5]。GA是一种群智能算法,通过随机化搜索过程在解空间中进行最优解搜寻。在搜寻最优解时,要求搜寻过程不仅要尽可能覆盖全局最优解(求泛能力),还要能够不断向当前局部最优解逼近(求精能力),而GA在求解过程中,并不擅长微调搜寻,故在GA中嵌套启发式算法,形成混合遗传算法。

图1 混合遗传算法构成示意图
在启发式方法中调度规则由于简单易实施、花费时间少等特点,更利用在实际生产中应用,因此本研究将调度规则嵌入到GA中,GA负责种群的进化,而调度规则根据GA得到的染色体构造与之所对应的解,设计出混合遗传算法。
根据Gere[6]的定义,调度规则是一个或者多个优先规则(启发式规则)的组合,调度规则用来将工件按照一定的排序准则或策略分配给机器。考虑实际生产排产的实施性,选取先到先服务调度规则(First In First Service,FIFS)进行混合遗传算法的设计。
2.1 编码解码策略
使用GA求解时,首先要选择合适的编码策略,将问题的解用染色体表示出来。为便于调度员安排生产调度,采用基于工件的编码方法。每个染色体都由n个代表工件编号的基因组成,所有工件的任意排列即构成一个可行调度,表示工件排产的优先次序。解码过程则按照编码中工件的先后次序进行生产,当一个处理机前有多个工件等待加工,采用FIFS规则进行加工。
2.2 种群的设计
每个染色体由n个代表工件编号的基因组成,解空间即为所有工件任意排列组成的序列。从这有n个基因组成的染色体中,随机生成一定数目的个体,选择表现较好的个体构成初始种群。对于种群规模的设置,太小会导致形成欺骗问题或陷入局部最优;而过大,虽然可以防止局部最优,但也会导致计算量的增加,降低算法效率。王小平和曹立明提出根据实际个体数量将种群规模设置为[20,100][7]。
2.3 选择操作
选择算子通过淘汰劣质个体,保证了种群在迭代过程中处于进化的状态。本文采用比例选择算子,计算某代群体中个体染色体的适应值在群体总适应值中所占的比例,即为该个体被选中的概率,根据轮盘赌选择方法进行选择,根据每轮产生的随机数[0,1],将多轮随机数作为选择指针来进行个体的选择,最后共同组成新种群。
2.4 交叉操作
交叉算子体现了生物进化过程中的基因重组过程,该过程保证群体中个体的品质得以提高。根据基于工件的编码策略,一个个体的染色体中不允许有相同的基因码,而基本遗传算法的交叉操作生成的个体一般不能满足约束,故采用部分匹配交叉的方法。
交叉概率pc决定交叉操作的频率,越大越易于收敛到最优解区域,但太高则会导致早熟收敛,一般在0.4~0.9的范围内进行取值[8]。
2.5 变异操作
在GA进化过程中,变异算子在一定程度上保证了种群的多样性。变异算子是一个单个体遗传操作算子,根据选定的变异概率pm对交叉后代集中的每个后代的每一位基因都进行变异操作,一般随机生成随机数r∈[0,1],根据r的取值将基因进行变异操作。
变异概率pm的选取可以增加样本模式的多样性,但是不能过高,以防退化为随机搜索,引发不稳定,所以通常设置较小,取值范围在0.001~0.1[8]。
3 钢结构车间HJSMT问题仿真研究
3.1 仿真流程设计
HJSMT是MTS问题和JSP问题的组合,既要求每道工序同时需要多台处理机进行加工(MTS问题的特点),又必须按照既定的加工先后顺序来进行(JSP问题的特点)。对于HJSMT问题的仿真,由于在仿真的过程中,工件使用移动对象MU进行表示,处理机使用SingleProc对象来表示,而要求一个实体同时占用多个处理机,这在仿真过程中是无法实现的。因此,如何实现一个实体同时占用多台处理机成为了HJSMT问题的仿真难点。
Yang, Pulat & Guan在对于MTS问题进行仿真求解的过程中,针对MTS问题需要同时占用多台处理器的问题,设计了通过复制实体的方法进行处理机的占用[9]。
但是对于MTS问题的研究都只有一道加工工序,而HJSMT问题则是有序的多道加工工序,因此在每道加工工序结束后,增加删除复制实体创建原实体的操作,以便根据作业实体完成有序的多道工序的加工。
流程图如图2所示。

图2 HJSMT问题仿真流程
3.2 仿真模型建立
1)规划项目的组织结构
新建仿真项目和HJSMT文件夹。如图,在文件夹中复制JOB对象,来定义JOBList中Job的类型。对JOB增加自定义属性Mnum,记录每道工序所需的处理机数量;Numorders属性记录每个工件的总的工序数量;step属性记录工件的工序;start属性则用来记录工序开始加工的时间。

图3 HJSMT仿真组织结构设计
2)建立仿真模型
仿真模型包含控制区和模型区。控制区用来控制整个模型的运行,在Frame中插入一个用来绘制模型外观的DrawRect方法,完成模型的外观绘制,同时添加控制区所需对象。模型区由CreateMode方法根据numMachines快速建立。
由于HJSMT的仿真过程存在多处理机任务问题,需要复制实体和删除复制体,因此根据零件的名字,由程序Init方法建立创建复制体的BFJi和删除复制体创建原实体的TMJi,加工时间均设置为0,BFJi的出口有方法PutA进行控制;当仿真结束后,由EndSim方法删除BFJi和TMJi。故BFJi和TMJi只在模型运行中出现,运行结束后删除。以numMachines=5为例,其仿真模型运行如图4所示。
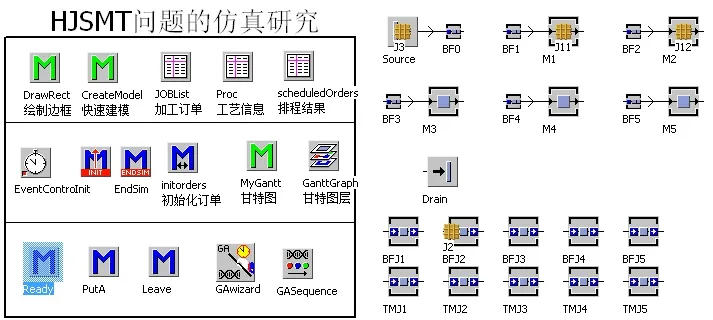
图4 HJSMT问题仿真模型
Ready方法控制BF0的输出,目的是将Source产生的工件对象送到对应的BFJi中,根据其加工所需的机器数量进行实体的复制;PutA则是判断是否所需处理机集合可用,然后将复制实体送到对应的处理机,完成工序的加工操作,同时将加工信息记录到scheduledOrders中。
工序加工结束后,处理机Mi在出口控制处调用Leave方法,复制实体前往对应的TMJi中,删除复制实体同时创建原实体,判断工件的下道工序。
JOBList表用来记录订单信息,即所需加工的零件信息,包含零件的类别、数量、名称等。Proc表用来记录零件的加工信息,包括每个零件的加工顺序、所需加工处理机、以及所需加工时间等。由于HJSMT问题每道工序需要多台处理机同时进行加工,且根据仿真流程,需要在加工前判断所有处理机是否可用,故Proc表设计如图5所示:第一列记录工件信息,第二列使用table类型来记录具体加工信息。加工信息表包含工序步骤、加工时间、加工所需处理机数量以及加工所需的具体处理机。

图5 Proc表设计
4 实验仿真与分析
4.1 算例验证
以一个n=5,m=5的HJSMT问题为例,其加工工序和所需加工时间如表1所示,括号中的数值即为该道工序所需加工时间,通过该算例对模型的有效性进行验证。
得到未进行优化前,即这5个工件按照顺序生产时,总的加工完成时间为340,调度甘特图如图6所示,利用本文提出的混合遗传算法,种群代数设置为100,采用De Jong[10]的经验数据对相关参数进行设置:种群规模为50,交叉概率pc为0.6,变异概率pm为0.001,对HJSMT问题进行优化求解。得到调度优化后总的加工时间为270,比优化前缩短了20.1%,得到新的生产顺序为:3 4 5 2 1,此时调度甘特图如图7所示。优化前后各处理机的设备利用率也都明显提高。
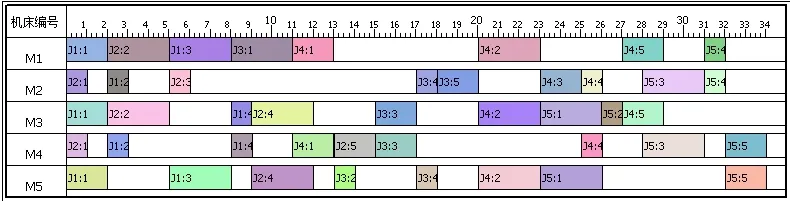
图6 初始调度甘特图
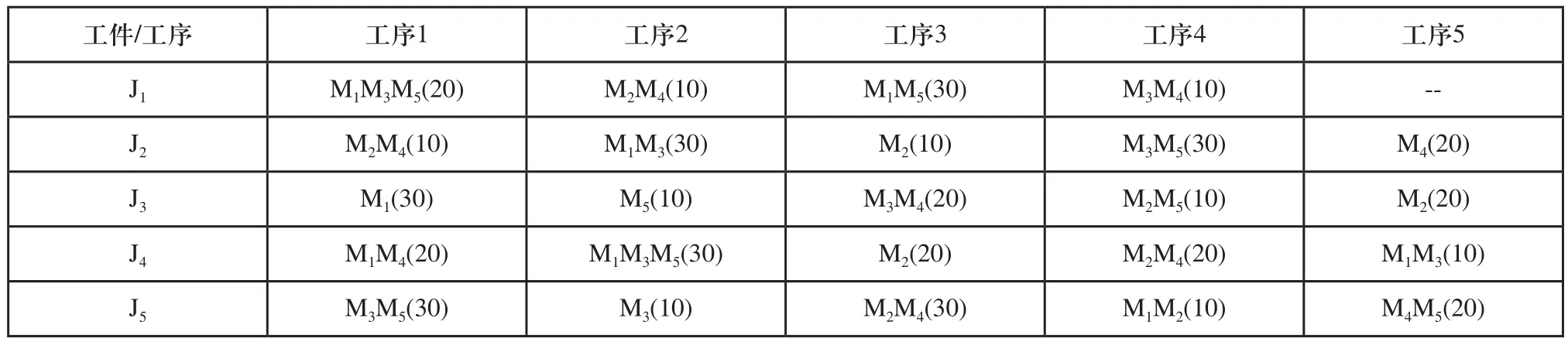
表1 n=5,m=5的HJSMT问题示例

图7 优化后甘特图
实验表明,该模型可以模拟具有多处理机任务约束的混合作业车间的生产过程,且可以利用遗传算法提供合理的优化调度。
4.2 实例模拟
T制造企业是一家以生产钢结构产品为主的制造企业,其结构车间以工人加工为主,生产中一般采用班组的划分形式,每个班组一般由6~8人组成,主要为焊工和铆工,也会增加1~2个打砂喷漆工,在实际生产中,车间会根据订单的数量、工作量的大小来调整运行的处理机的数量。
以吊梁机金属结构的部分零件为例,表2给出了其零件加工工艺信息。
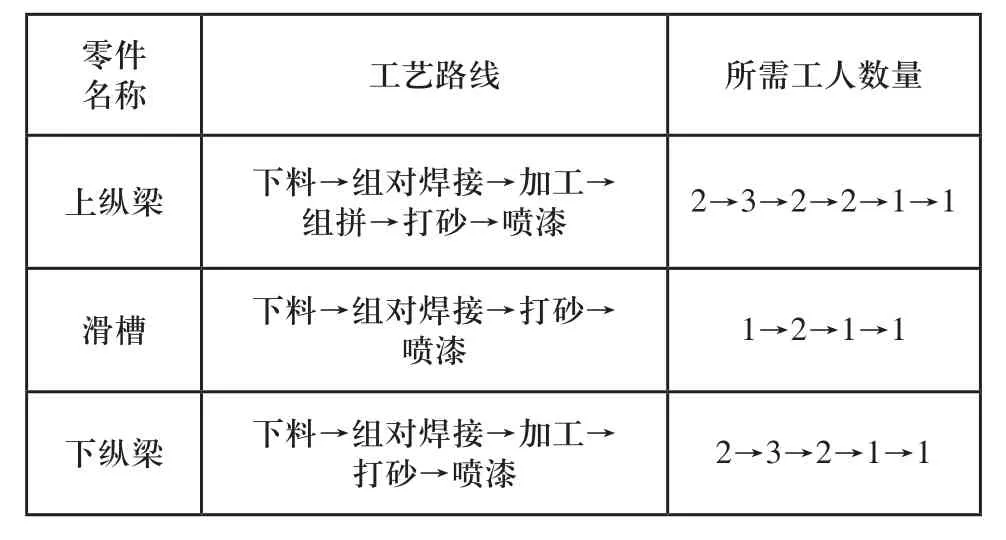
表2 金属结构部分零件加工工艺信息
根据车间生产情况,令仿真模型numMachines=6,即班组工人为M1-M6。这3个零件记为J1-J3,其加工工艺路线如表3所示,括号内的数字代表其加工时间(单位:h),将其输入本文建立的仿真模型中。
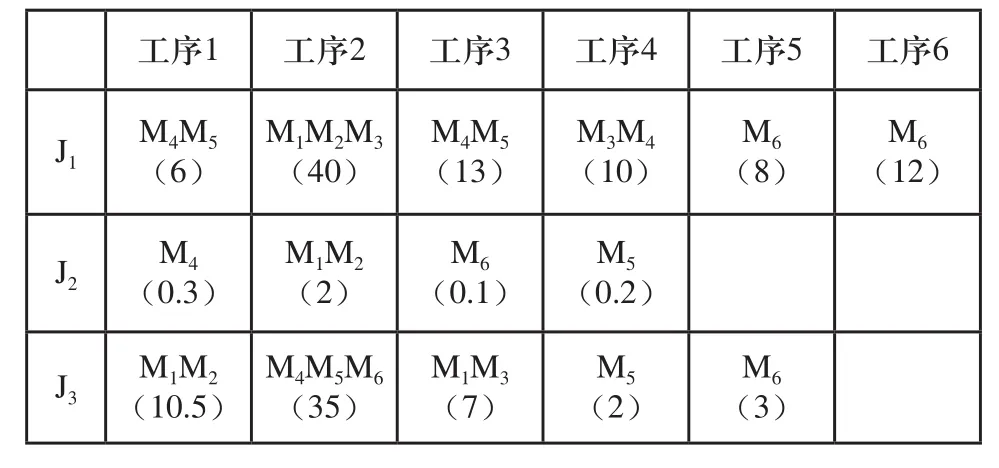
表3 金属结构大型零件工艺信息表
按照企业原来顺序生产计划,其时间安排为3月17日~3月29日,共13天完成生产。按照每天工作时间8小时,完成这3个零件的制作共需104小时,而采用本文的仿真优化模型,得到新的调度安排为:2 3 1,调度甘特图如图8所示,总完工时间为95.5小时,生产时间缩短8.2%。
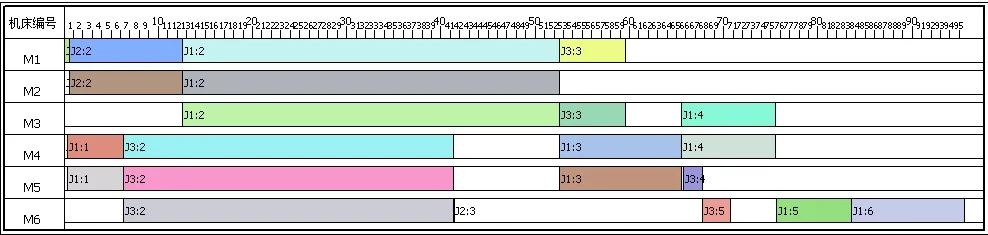
图8 调度甘特图
5 结束语
随着越来越多的制造企业通过采用多处理机任务的生产方式来提高生产效率的车间制造,对于混合多处理任务的作业车间调度研究具有十分重要的意义,而多处理机任务作业车间调度是多处理机任务调度和作业车间调度问题的结合,由于问题的复杂性导致直至目前研究成果仍然较少。
本文针对钢结构车间具有多处理机任务约束的混合作业车间调度(HJSMT)问题进行仿真研究,对JSP问题增加多处理机任务(MTS)的约束,针对HJSMT问题进行抽象,建立数学规划模型,然后结合JSP和MTS问题的特点,建立HJSMT仿真优化模型,并通过算例对模型的有效性进行验证。结果表明,该优化模型能对HJSMT问题进行有效排产,提高企业生产效率。同时,为了适应制造企业车间变化的生产环境,设计快速建模方法,根据处理机数量快速生成问题的仿真模型,模型使用操作简单,且基于工件编码的调度结果便于理解与实施。本文的仿真模型基于特定假设,然而实际生产中往往会有各种不确定因素,如机器故障、工件插入等,后续也将不断完善模型,更好地服务制造生产。
