金属螺旋波导中几何相位对SPP本征模的调制

蒋 然 易向东

(首都师范大学物理系，北京 100048)

0 引 言

金属表面等离子体(surface plasmon polariton，简称SPP)是一种在金属—电介质界面附近的表面波，它沿着金属表面传播，离开界面迅速衰减.由于SPP的奇特性质，近年来它成为了一个重要的研究方向并有了很多应用[1-4].然而，对SPP几何相位的许多问题还有待深入研究.几何相位是一个只和系统演化路径的几何性质有关的相位，1984年，Berry考虑了绝热演化的量子系统，从薛定谔方程出发，推导得到了Berry相位[5].从此之后，人们对这种和系统演化路径有关的几何相位产生了浓厚的兴趣.1986年，Chiao等提出利用螺旋光纤引导光传播可以获得一个几何性质的相位，并成功地在实验上观察到了该相位[6-7]；1987年，Bitter等研究了中子的几何相位[8]，之后，陆续有很多学者研究了不同系统的几何相位[9-10].由于几何相位和系统演化路径的几何性质有关，因此，在应用SPP的过程中，SPP的传播有可能导致几何相位的产生.或者说，可以利用几何位相对SPP波进行调制，而这种调制无疑具有重要的应用价值.本文解析计算了螺旋金属管包裹介质芯波导中的SPP本征模，又在绝热近似条件下计算了不同本征模应当附加的几何相位.在此基础上得到了经过螺旋管之后的本征波函数.本工作展示了几何位相对于SPP的影响，给出了直观的物理图像.

1 具有旋转对称截面的金属波导中的SPP

为了使SPP产生几何相位，需要利用横截面旋转对称的SPP波导.本文采用电介质内核——金属包层波导结构[11]，如图1所示.

图1 电介质环境中的电介质内核——金属包层波导结构

在柱坐标系(r,θ,z)下求解麦克斯韦方程组，可以得到电磁波本征模.对于均匀且各向同性的介质构成的柱状区域，在高斯单位制下求解麦克斯韦方程组得[1]：

(1)

图1所示的波导结构中的场量用分段函数表示如下：

(2)

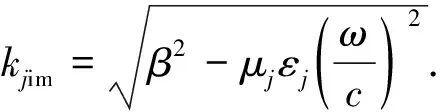
(3)

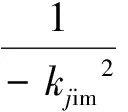
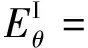
(4)

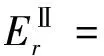
(5)

(6)

下面利用边值关系和初始条件求解色散关系和待定系数.将界面两边的电场、磁场用下标1、2区别，对该模型而言，没有自由电荷和自由电流，边值关系为[15]：

(7)

对时谐波而言，(7)式中后两式可由前两式推导得到[15].因此，只有前两式独立，使用边值关系时，只需使切向电场、磁场连续即可.对于上述结构的SPP波导，边值关系为：

(8)

det[M]=0．

(9)

选取金属包层材料为银，核心及环境的电介质εI=εⅢ=10，波导尺寸RI=85 nm，RⅡ=90 nm，对此波导应用上述方法求解待定系数.当SPP的光子能量为2.1 ev时，可以得到1～5阶模SPP的β和待定系数，见表1．

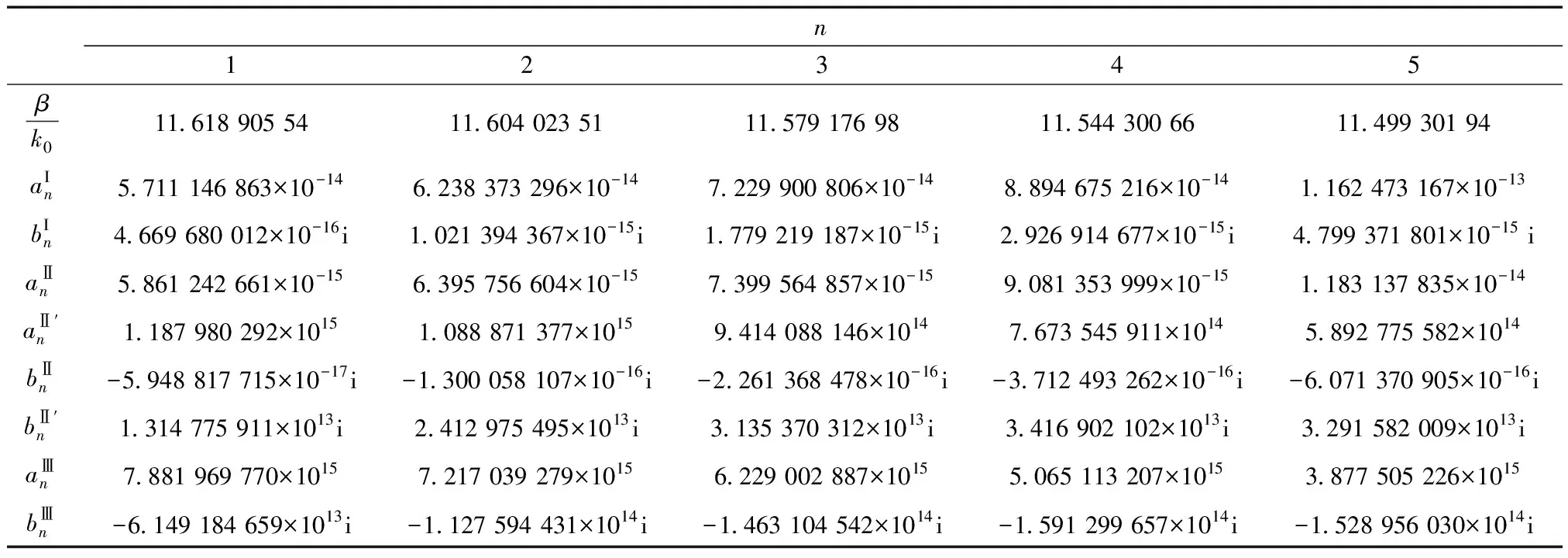
表1 SPP 1～5阶模的波矢及场量的系数

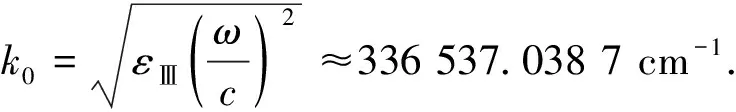
下面说明各阶SPP的特点.由于各场量对r的依赖关系不明显，所以我们以一阶模为例，将此依赖关系展示在图2中.

图2 SPP 1阶模场量随r的分布，横轴为r，纵轴为各场分量的大小

由图2可知，电磁场在离开金属表面后急剧衰减，这符合SPP的特点.其它阶模式对r的依赖关系也类似.然而，不同阶SPP对θ的依赖关系却有着较大区别.图3以Er为例展示了场量在SPP波导横截面中的分布：

图3 SPP波导z=0横截面中的Er场分布：(a)～(e)分别为1～5阶模SPP的Er的场分布.图中的颜色表示的振幅，红色表示场沿正方向；蓝色表示场沿负方向.

可以看到，随着SPP阶数的上升，Er随θ变化而变化的周期变小.其它分量对θ的依赖关系随着阶数的上升也有着类似的变化.这是由于场量中都含有因子ei(nθ+βz-ωt)，n越大，相同的θ所引入的相位就越大，即场量随θ变化而变化得越快，故场量随θ分布的周期就越小.

以上讨论的是轴线为直线的旋转对称结构波导中的SPP本征模.对于具有上述旋转对称结构的弯曲SPP波导，如果保证其中的SPP绝热地传播，即本征模之间不相互转化，则波导中的本征模仍然可以用(4)～(6)式表示，只需将其中的z替换为沿着轴线距波源的距离l即可.因此，当波导仍然由银和εI=εⅢ=10的材料构成，且RI=85 nm，RⅡ=90 nm，光子能量为2.1 ev时，待定系数仍为表1中的数值.

2 SPP在螺旋波导中的传播与场分布在参数空间中的平移

|B|=|∬DKdσ|，

(10)

式中，K表示曲面的Gauss曲率，dσ表示面积分元，D表示闭合曲线C在曲面S上围出的曲面区域.

当上述曲面为球面时，设球面为Sβ，如图4所示，其中oimmobile-ximmobileyimmobilezimmobile为实验室坐标系.此时，(10)式中的Gauss曲率K为球面半径平方的倒数.若沿Sβ上的一条闭曲线平移矢量一周后，与平移前相比的角度差别为：

(11)

式中，R表示球面Sβ的半径，Ω表示闭曲线围出曲面所对的立体角.当闭曲线由φ为常数的点构成时，将此闭曲线记为Cβ，则：

=2π(1-cosφ).

(12)

因此，

|B|=2π(1-cosφ)．

(13)

图4 球面Sβ及oimmobile-ximmobileyimmobilezimmobile坐标系

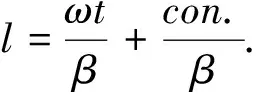
图5 (a)SPP波导横截面的双层结构； (b)SPP螺旋波导的整体结构

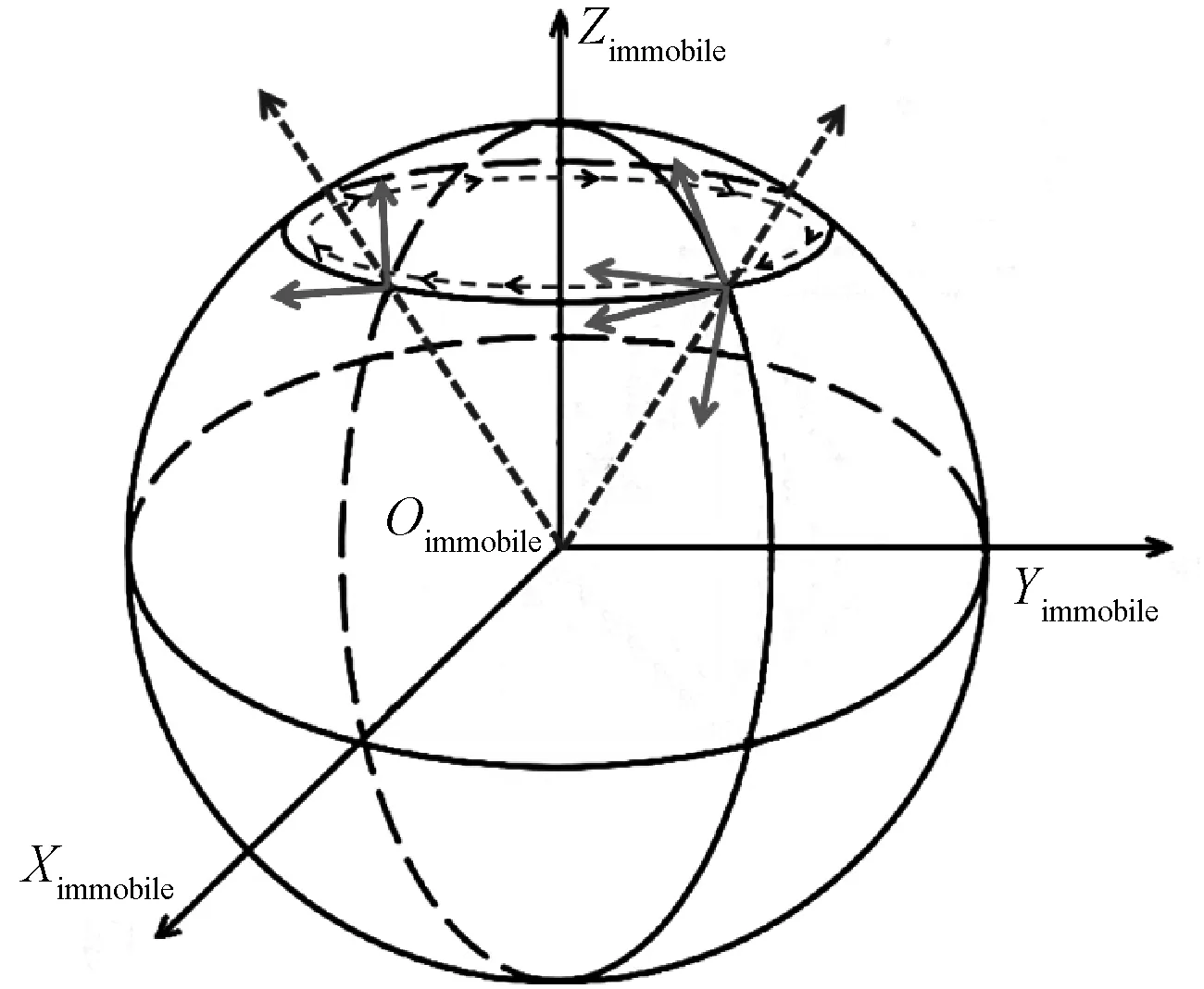
图6 蓝色虚线箭头为球面的法向，红色坐标系xoy切于球面，绿色坐标系为平移一周后的坐标系xoy

综上所述，在保证SPP在螺旋波导中绝热地传播时，场分布的旋转角度的正负只与波导的螺旋方向有关，大小只与演化路径即螺旋波导的整体的形状有关，而与局域部分的半径等几何参数、螺旋波导的大小以及波导材料等因素均无关.

3 螺旋波导中SPP的几何相位

根据上述讨论，SPP在图5所示的螺旋波导中传播一周，场分布在波前所在横截面中整体旋转B=-2π(1-cosφ)角度.显然，如果SPP传播N周，场分布会旋转NB=-2πN(1-cosφ)角度，这个旋转角度还不是相位，接下来我们从场分布的旋转和SPP本征模表达式出发推导出几何相位.上述波导中的n阶SPP场量都具有如下形式：

F(r,θ,l,t)=F0(r)·einθ·ei(βl-ωt)．

(14)

根据第三部分的讨论可知，场分布的旋转会导致θ发生变化，变为θ-NB，所以将(14)式中的θ替换为θ-NB后就可得到SPP在螺旋波导内传播N周后的场分布：

F(r,θ,l,t)=F0(r)·ein(θ-NB)·ei(βl-ωt)．

(15)

令

γ=nNB=±2πnN(1-cosφ)，

(16)

将(16)式代入(15)式并进一步处理，可得：

F(r,θ,l,t)=F0(r)·einθ·ei(βl-ωt)eiγ，

(17)

比较(14)和(17)式可知，SPP在螺旋波导中传播N周后，所有场分量除了动力学相以外，都会多出一个相位：γ=±2πnN(1-cosφ)，对确定的SPP本征模，这个相位只和演化路径的几何特征即螺旋波导整体几何形状有关，这就是几何相位.

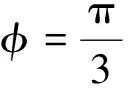
表2 SPP1～5阶模的场量旋转角度及几何相位

图7 Er在垂直于波导轴线的横截面中的分布图.上一行：只考虑动力学相位；下一行：同时考虑动力学相位和几何相位

4 结 论

电磁波产生几何相位的关键在于：场量分布与垂直于轴线的横截面中的方向有关，并且波导材料及波导边界各向同性，使得波导对场分布无轴向的广义力矩的作用，场分布可以在垂直于传播方向的横截面中自由转动.当SPP绝热地在螺旋波导中传播N周后，产生大小为|γ|=2πNn(1-cosφ)的几何相位，该相位的大小只与角度φ即波导的形状有关，正负只与波导的螺旋方向有关，可见这个相位明显的几何特性.

图8 垂直和平行于波导轴线的截面中的场分布，(a)列和(b)列分别是垂直于轴线的截面中的电场和磁场分布；(c)列和(d)列分别是平行于轴线的截面中的电场分布和磁场分布.