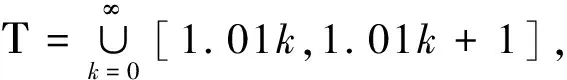时间尺度上一类Leslie-Gower捕食模型持久性及概周期解的存在性
2018-12-28李建祥
李 玲 李建祥
(保山学院数学学院,云南 保山 678000)
1 问题背景
近年来,许多专家和学者研究了具有Holling-type Ⅱ类功能性反应的修正Leslie-Gower捕食模型
其中,x(t)表示t时刻食饵总数,y(t)表示t时刻的捕食者总数,ri(t),ai(t),b(t)(i=1,2)都是为非负连续的周期函数,ki(i=1,2)为常数,具体的生物含义见文献[1].例如文献[1]利用线性周期脉冲方程中的Floquet理论研究了上述模型的动力学行为.文献[2]利用重合度理论和通过建立合适的Lyapunov函数得到该系统正解的存在性和全局吸引性等.
1990年,德国数学家Stefan Hilger在他的博士论文中建立了时标理论,即一种连续和离散计算的统一方法.考虑到概周期现象较周期现象更为常见、自然界会受到人类的开采等因素的影响以及非自治系统更能精确地描述实际情况,本文研究时标上具反馈项和Holling-type Ⅱ类功能性反应的修正Leslie-Gower捕食模型
(1.1)
其中,t∈Τ,Τ为概周期时标,x(t)表示t时刻食饵总数,y(t)表示t时刻的捕食者总数,u(t)、v(t)为反馈控制项,ri(t)、ai(t)、b(t)、ci(t)、di(t)、ki(t)、αi(t)、βi(t)(i=1,2)为时标Τ上的非负有界概周期函数.从生态学的角度来看,假设系统(1.1)满足初始条件:x(0)>0,y(0)>0,u(0)>0,v(0)>0.
注1.1 令N(t)=ex(t),M(t)=ey(t).
当Τ=R时,系统(1.1)具有如下连续形式:
当Τ=Z时,系统(1.1)具有如下离散形式:
据我们所知,还没有文献讨论过系统(1.1)的持久性和存在概周期解的问题.本文主要目的是利用Lyapunov函数和微分不等式,得到该系统持久和存在概周期解的充分条件.
通篇假设:
(H1)ri(t)、ai(t)、b(t)、ci(t)、di(t)、ki(t)、αi(t)、βi(t)(i=1,2)为时标Τ上的非负有界概周期函数,即0≤rim≤ri(t)≤riM,0≤aim≤ai(t)≤aiM,0≤bm≤b(t)≤bM,0≤cim≤ci(t)≤ciM,0≤dim≤di(t)≤diM, 0≤kim≤ki(t)≤kiM,0≤αim≤αi(t)≤αiM,0≤βim≤βi(t)≤βiM,i=1,2且-bM,-αiM∈R+.

2 预备知识及引理
定义2.1[3]称时间尺度Τ是概周期的,如果Π:={τ∈R:t±τ∈Τ,∀t∈Τ}≠{0}.
定义2.2[3]令Τ为一概周期时间尺度.称函数f∈C(Τ,Εn)是Τ上概周期的,如果对于任意给定的ε>0,集合E(ε,f)={τ∈Π:|f(t+τ)-f(t)|<ε,∀t∈Τ}是相对稠密的,即对任给的ε>0,存在l(ε)>0使得每个长度为l(ε)的区间内至少包含一个τ(ε)∈E(ε,f)使得|f(t+τ)-f(t)|<ε,∀t∈Τ.集合E(ε,f)称为f(t)的ε-移位数集,称为f(t)的ε-移位数,l(ε)>0称为E(ε,f)的包含区间长.
定义2.3[4]称系统(1.1)具有持久性,若存在独立于系统(1.1)的解的正常数mi,Mi(i=1,2,3,4),使得系统(1.1)的任意解(x(t),y(t),u(t),v(t))T都满足
引理2.1[5]设-a∈R+.

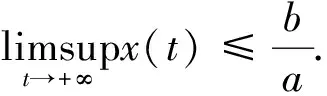

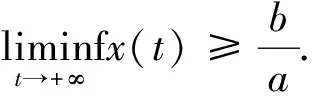
引理2.2[5]假设在Τ×S×S上存在Lyapunov函数V(t,X,Y)满足下面的条件:
a(‖X-Y‖0)≤V(t,X,Y)≤b(‖X-Y‖0),
其中a,b∈K,K={a∈C(R+,R+):a(0)=0,且a是增函数};
(2)|V(t,X,Y)-V(t,X1,Y1)|≤L(‖X-X1‖0+‖Y-Y1‖0),其中L>0是一个常数;
(3)D+VΔ(t,X,Y)≤-cV(t,X,Y),其中-c∈R+,c>0;
此外,如果系统(1.1)存在一个解(x(t),y(t),u(t),v(t))T∈S,其中S是一个紧集,则系统(1.1)有唯一的概周期解,且此概周期解还是一致渐近稳定的.
3 持久性
在这一节,利用不等式放缩,我们将研究系统(1.1)的持久性.

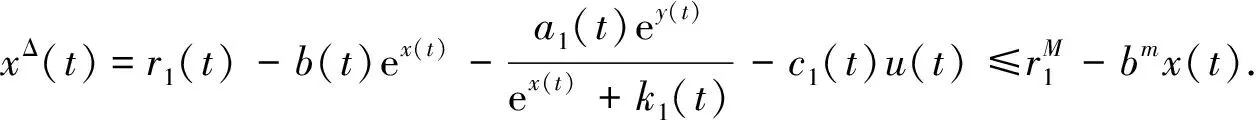
从上式可知,对任给的ε>0,存在t1∈Τ,使得x(t)≤x*+ε,对于t>t1都成立.因此,当t>t1时
uΔ(t)=d1(t)-α1(t)u(t)+β1(t)ex(t)≤
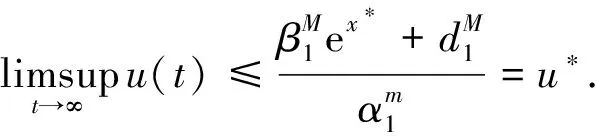

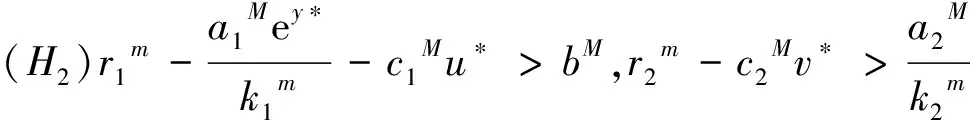
证明:假设(x(t),y(t),u(t),v(t))T为系统(1.1)的解.对任意ε>0,由定理3.1知,存在t2∈Τ,使得x(t)≤x*+ε,y(t)≤y*+ε,u(t)≤u*+ε,v(t)≤v*+ε对于t>t2都成立.
由系统(1.1)的第一个方程和条件(H1)得,
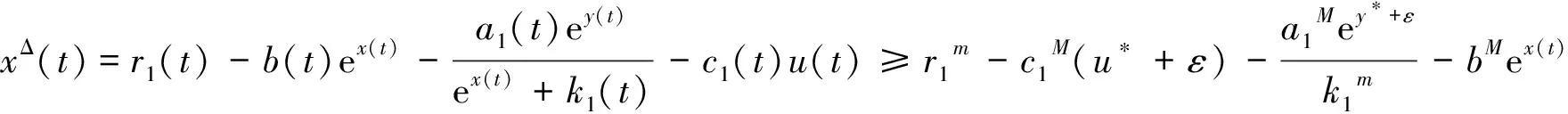

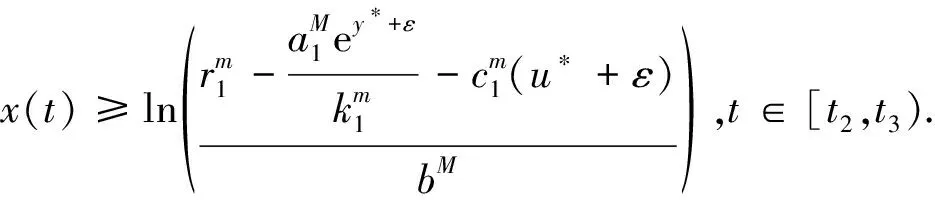




定理3.3假设条件(H1)和(H2)成立,则系统(1.1)是持久的.
推论3.1假设条件(H1)和(H2)成立,则系统(1.1)对应的连续系统和离散系统也是持久的.
4 概周期解的存在性和稳定性
假设Ω是系统(1.1)的所有解(x(t),y(t),u(t),v(t))T组成的集合,对于所有t∈Τ满足x*≤x(t)≤x*,y*≤y(t)≤y*,u*≤u(t)≤u*,v*≤v(t)≤v*.易知,Ω是系统(1.1)的不变集.
定理4.1假设条件(H1)和(H2)成立,则Ω≠∅.
证明:由于ri(t),ai(t),b(t),ci(t),di(t),ki(t),αi(t),βi(t)(i=1,2)为时标上的概周期函数,则存在序列{τn},当n→∞时,有τn→∞,使得ri(t+τn)→ri(t),ai(t+τn)→ai(t),b(t+τn)→b(t),di(t+τn)→di(t),ki(t+τn)→ki(t),αi(t+τn)→αi(t),βi(t+τn)→βi(t),i=1,2.
由定理3.1和定理3.2,知对任给的ε>0,存在t0∈Τ,使得当t>t0时,有
x*+ε≤x(t)≤x*+ε,y*+ε≤y(t)≤y*+ε,
u*+ε≤u(t)≤u*+ε,v*+ε≤v(t)≤v*+ε.
记xn(t)=x(t+τn),yn(t)=y(t+τn),un(t)=u(t+τn),vn(t)=v(t+τn),t>t0-τn,则对任意的正整数m,存在函数序列{xn(t):n≥m},{yn(t):n≥m},{un(t):n≥m},{vn(t):n≥m},使得它们在时标Τ上的任意有限区间上有收敛子列.为方便起见,其收敛子列依然记为{xn(t):n≥m},{yn(t):n≥m},{un(t):n≥m},{vn(t):n≥m}.
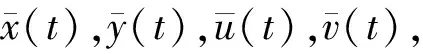
由于ε为任意小的正数,令ε→0有
定理4.2假设条件(H1)和(H2)成立,进一步假设(H3)c>0,-c∈R+,
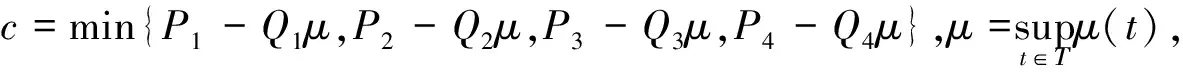
则系统(1.1)存在唯一的概周期解(x(t),y(t),u(t),v(t))T∈Ω,且此概周期解是一致渐近稳定的.
证明:由定理4.1知,系统(1.1)有一有界解(x(t),y(t),u(t),v(t))T满足
0 0 ∀t∈Τ. 则|x(t)|≤A1,|y(t)|≤A2,|u(t)|≤A3,|v(t)|≤A4,其中A1=max{x*,x*}, A2=max{y*,y*},A3=max{u*,u*}, A4=max{v*,v*}. 对任意的(x(t),y(t),u(t),v(t))T∈R4,定义范数 考虑系统(1.1)的乘积系统 (4.1) 在Τ×Ω×Ω上定义Lyapunov函数 V(t,X,Y)=(x(t)-p(t))2+(y(t)-q(t))2+ (u(t)-w(t))2+(v(t)-z(t))2. 易知范数 与范数 ‖X-Y‖*= 等价,即存在常数C1>0,C2>0,使得C1‖X-Y‖≤‖X-Y‖*≤C2‖X-Y‖.因此,(C1‖X-Y‖)2≤V(t,X,Y)≤(C2‖X-Y‖)2. 此外,对X1=(x1(t),y1(t),u1(t),v1(t))T,Y1=(p1(t),q1(t),w1(t),z1(t))T有 |V(t,X,Y)-V(t,X1,Y1)|=|(x(t)-p(t))2+ (y(t)-q(t))2+(u(t)-w(t))2+ (v(t)-z(t))2-(x1(t)-p1(t))2- (y1(t)-q1(t))2-(u1(t)-w1(t))2- (v1(t)-z1(t))2|≤ |(x(t)-p(t))+(x1(t)-p1(t))|· |(x(t)-p(t))-(x1(t)-p1(t))|+ |(y(t)-q(t))+(y1(t)-q1(t))|· |(y(t)-q(t))-(y1(t)-q1(t))|+ |(u(t)-w(t))+(u1(t)-w1(t))|· |(u(t)-w(t))-(u1(t)-w1(t))|+ |(v(t)-z(t))+(v1(t)-z1(t))|· |(v(t)-z(t))-(v1(t)-z1(t))|≤ L{(|x(t)-x1(t)|+|y(t)-y1(t)|+ |u(t)-u1(t)|+|v(t)-v1(t)|)+ (|p(t)-p1(t)|+|q(t)-q1(t)|+ |w(t)-w1(t)|+|z(t)-z1(t)|)}= L{‖X-X1‖+‖Y-Y1‖},其中L=4max{A1,A2,A3,A4}. 因此,满足引理2.2的条件(2). 沿系统(1.1)的解计算V(t,X,Y)的右上导数得, D+VΔ(t,X,Y)=[2(x(t)-p(t))+ μ(t)(x(t)-p(t))Δ](x(t)-p(t))Δ+ [2(y(t)-q(t))+μ(t)(y(t)-q(t))Δ]· (y(t)-q(t))Δ+[2(u(t)-w(t))+ μ(t)(u(t)-w(t))Δ](u(t)-w(t))Δ+ [2(v(t)-z(t))+μ(t)(v(t)-z(t))Δ]· (v(t)-z(t))Δ. V1+V2+V3+V4. 利用微分中值定理,有ex(t)-ep(t)=eξ(t)(x(t)-p(t)),ey(t)-eq(t)=eη(t)(y(t)-q(t)),其中ξ(t)介于x(t)与p(t)之间,η(t)介于y(t)与q(t)之间. 则(4.1)可改写为 则 则有 D+VΔ(t,X,Y)=V1+V2+V3+V4 因此,满足引理2.2的条件(3).故系统(1.1)有唯一的一致渐近稳定的正的概周期解. 推论4.1假设条件(H1)、(H2)和(H3)成立,则系统(1.1)对应的连续系统和离散系统有唯一的正的概周期解,且这个概周期解是一致渐近稳定的. 例5.1考虑如下系统
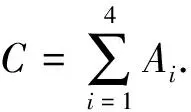

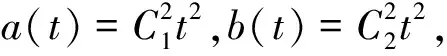

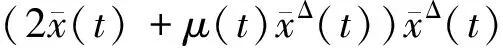


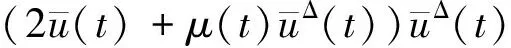

5 例 子