有限理性用户风险态度对系统效率的影响

魏庆琦，肖 伟

(1.重庆交通大学经济与管理学院，重庆400074；2.电子科技大学经济与管理学院，成都610054)

0 引言

不确定交通网络均衡作为城市交通网络研究和管理策略设计的基础，是近年来交通网络均衡研究领域的热点[1-9].但是，现有的不确定网络均衡分析存在割裂：一部分研究认为城市路网不确定性来自随机路网能力退化[1-2]；还有部分研究者认为不确定性来自出行用户的有限理性，即用户没有能力搜集和正确处理所有的即时路网信息[3-8].这些研究分别从外部客观环境[1-2]和用户内部行为[3-8]两个方面出发，孤立地定义和分析城市交通系统的不确定性[1-3]，其理论有待改进.同时，随着累积前景出行效用(Cumulative Prospect Value,CPV)理论的发展，由于单参考点模型简单地将出行时间轴划分为早到收益和迟到损失两个区域，没有考虑到用户既存在迟到损失，也存在早到损失[3-4].因此，单参考点模型逐渐被双参考点模型取代[3-4].近年来，也有少量研究试图将城市路网的客观不确定性和主观不确定性结合起来，比如王倩等[9]结合能力退化路网和单参考点CPV模型，分析了两个特殊风险态度取值下UE网络的分布特征，但是该研究基于单参考点效用模型，在用户风险态度分析时也仅简单讨论了两种独立的情况.

以上文献分别从外部客观环境和内部有限理性两个方面探讨城市路网均衡的不确定性，但仍存在以下问题：①对于路网不确定性来源的分析存在割裂，认为其要么来自客观环境[1-2]，要么来自用户主观能力限制[3-8]，没有将两者相结合；②少量将内外不确定性结合考虑的研究以单参考点模型为基础[9]；③没有深入分析连续异质用户风险态度对网络均衡和系统效率的影响[9].针对这些问题，本文结合能力退化路网和双参考点CPV模型，构造考虑路网退化和连续风险态度的双参考点用户均衡模型，证明模型解的存在性并设计了相应的嵌套算法.最后将模型应用于Nguyen&Dupuis路网，分析了连续风险态度对网络均衡和系统效率的影响.

1 连续风险态度双参考点择路模型

1.1 基于CPV的双参考点到达时间感知价值

借鉴相关研究[4-5]，将基于CPV理论的双参考点累积到达时间感知价值(Arrive Time Cumulative Perceived Value，ATCPV，下文简称CPV)效用模型介绍如下：如图1所示，横坐标为时间，纵坐标表示不同时间点对应的CPV.时间轴上共有4个关键点，0点表示出发时间Tdepart，工作开始时间点Twork位于最右方，这两个点都是外生可观测的；最早到达时间参考点Tearly和最佳到达时间参考点Tstar由左至右位于Tdepart和Twork之间，具有内生不可观测性，由用户风险态度和各路段出行时间分布决定.Tearly和Tstar是本文主要研究的两个内生参考点，它们与外生Tdepart和Twork一起，将用户行程时间轴划分为4个到达时间感知价值区间：I区，早到负效用区；II区，早到正效用区；III区，晚到正效用区；IV区，晚到负效用区.当到达时间落在不同时间区域，将产生不同的效用：落在I区时，表示到达时间过早，产生负效用；落在II、III区时，表示到达时间合理，产生正效用；落在IV区时，表示迟到并获得负效用.由于个体存在面临收益时风险规避、面临损失时风险偏好的特点，负效用曲线比其相对的正效用曲线更加陡峭.同时，由于II区存在上限约束，它通常比III区更加狭窄.因此，4个区的CPV曲线均为非对称曲线.

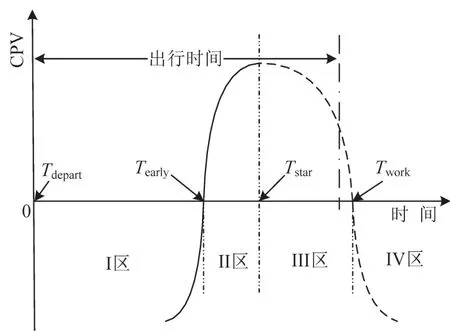
图1 双参考点CPV分区图Fig.1 Partitions of arrive time perceived value with double reference points

因此，将OD对r(r∈R)间，路径k(k∈K)的CPV值描述如下：和分别为 4 个时区的上下限；表示时区，当到达时间落在i区时δi=1，否者表示OD对r之间选择路径k出行到达时间落在i区时的感知价值；为时区i的决策权重，gi(t)为时区i的价值函数.

根据CPV理论，当事件发生的客观实际概率为φ时，4个时区的主观感知概率分别为

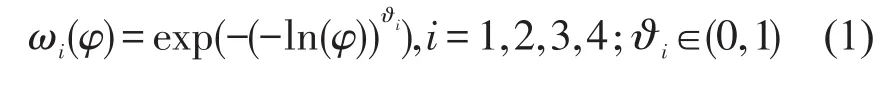
到达时间tj落在区间i时的决策权重为

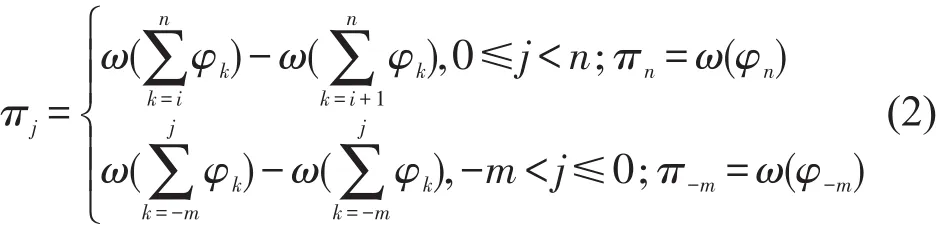
在到达时间连续随机分布时，令f(t)和F(t)分别为到达时间概率密度函数和累积概率密度函数，则有

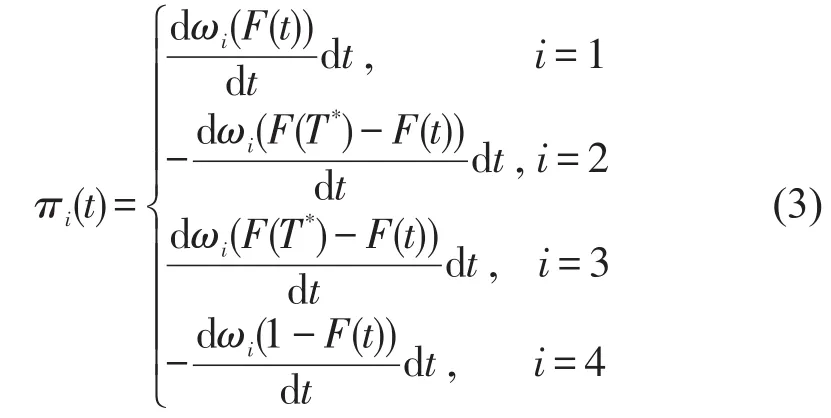
按照时区划分的价值函数为

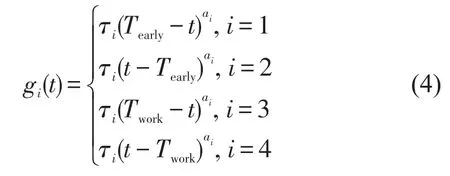
式中：αi∈(0,1)决定各时区价值函数的形状；τi表示价值函数的正负和陡峭程度.

由于价值函数在I、IV两区取负，II、III两区取正，有：τ4＜τ1＜0＜τ2＜τ3.根据有限理性行为理论，Tstar处获得最高收益，其两端正区间的晚到收益大于早到收益，且早到收益区存在上限，则Tstar-Tearly≤.同时，针对同一参考点的收益，个体对损失更加敏感，因此有-τ1＞τ2,-τ4＞τ3.

1.2 连续风险态度下的用户双参考点取值

随机交通网络中，连续风险态度用户参考点取值依赖于路网随机性和用户风险态度.本模型为单类用户模型，依据连续风险态度分别计算当路网中各路段出行时间服从正态分布时，根据路段时间随机分布，获得路径时间期望和标准方差，当OD对r(r∈R)间用户不迟到的概率最低要求为σr时，可以获得路径k最佳到达时间参考点为

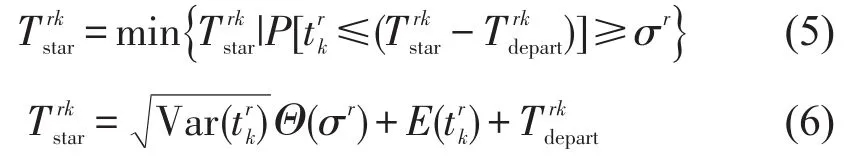
式中：Θ(·)为标准正态分布累积概率密度函数的反函数.

由于II区比III区更狭窄，且存在与个体社会经济特性、风险态度和不迟到最长出行时间相关的上限系数ϕ.

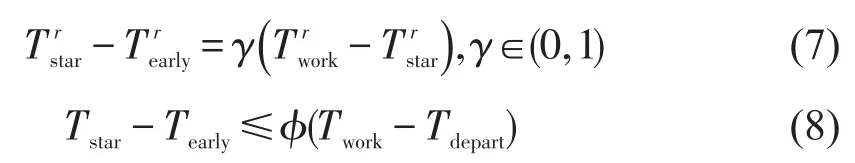
1.3 考虑路网退化的BPR路段出行时间分布

BPR(Bureau of Public Roads)路段时间模型中，ta为路段a随机出行时间，为零流时间，xa为路段a即时流量，λ和β为外生参数，Ca为随机路段通行能力.

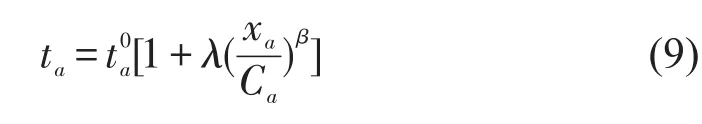
当路网随机退化时，Ca服从间的均匀分布[1].为路段设计能力上限，θa为路网能力保有系数，为路段随机能力退化下限.与常见的随机网络均衡模型(SUE)不同，随机退化的路段通行能力是路段通行时间随机性的外部原因，而SUE中用户时间感知的随机性是路段通行时间随机性的内部原因.

此时路段时间的期望和方差分别为

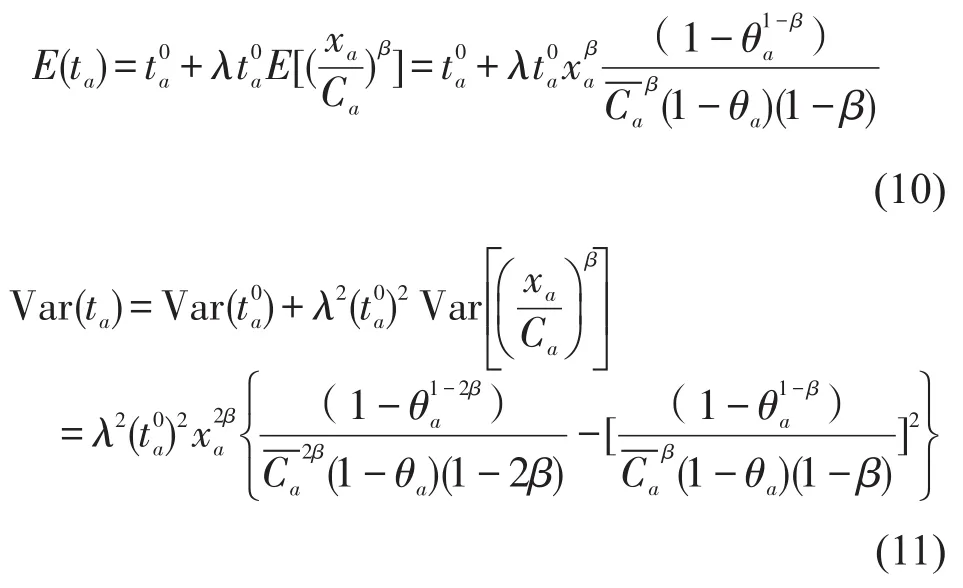
当路段时间相互独立时，则OD对r之间路径k的时间为，是OD对r之间的路段/路径关联系数.由于各路段时间分布符合林德伯格—费勒(Lindeberg-Fellercentral Limit Theorem)条件[3]，路径时间服从正态分布[1]，即

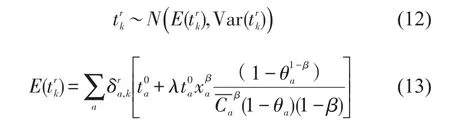
综上所述，可得

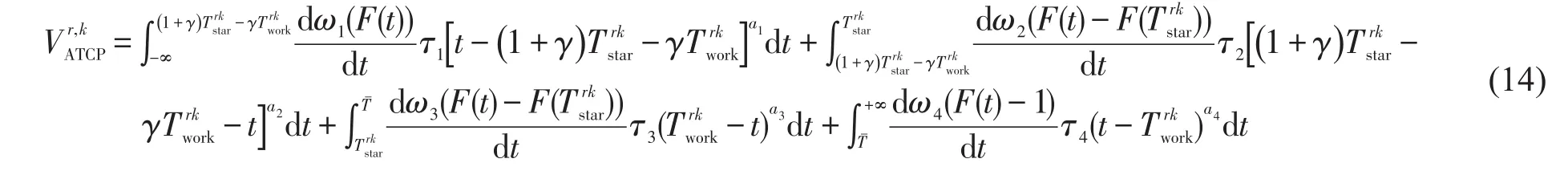
2 连续风险态度下双参考点退化网络均衡模型

2.1 用户均衡条件与均衡解

由于可行路径集Γ为紧凸集，存在任意f∈Γ，总存在唯一最近可行点p(f)∈Γ使f投影于Γ.定义一个映射，则当且仅当θ(f)=f时，有f是CPV-UE的一个均衡解[4，9].由于路径出行时间、路段退化系数，以及到达时间价值函数和感知概率权重函数均为连续函数，因此CPV函数ψ(·)为连续函数，则θ(·)也连续，且满足Brouwer不动点定理[3，6]，VI均衡解存在.

2.2 系统最优模型与求解方法

由于随机路网中用户CPV不可观测，因此系统最优SO模型仍然以网络出行时间期望最小为目标函数.考虑路网能力退化的随机SO均衡模型为

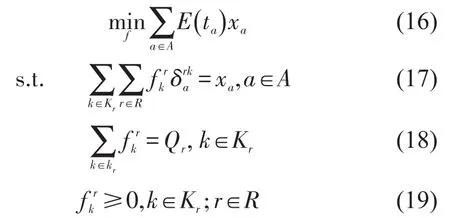
式中：xa为SO均衡时的路段流量,a∈A；E(ta)=E[ta(xa)]为相应SO均衡下的路段通行时间，a∈A，E(ta)由式(13)获得.SO均衡解可通过Frank-Walfe法[10]求得，由于篇幅所限，此处不再赘述.

2.3 系统效率分析模型

从平均时区宽度TZWi、平均到达时间累积感知价值TPV、平均路径时间标准差TSD和平均路径时间期望TE这4个角度对系统效率进行分析.由于IV区指到达时间晚于工作开始时间，无理论上限，因此不对其宽度进行分析.系统分析模型具体表示为

3 求解算法

基于相继平均法(Method of Successive Averages,MSA)和Frank-Walfe法设计两阶段启发式算法，求解双参考点CPV_UE模型和路网随机退化的SO模型.

具体算法步骤如下：

首先确定系统参数，收敛指标ε，最大迭代次数Nmax.

Stage AMSA法求CPV_UE均衡解.

Step A1初始化.以深度遍历法搜索并建立OD对可行路径集.在路网零流状态下计算各路径.执行0-1加载，获得初始路段流量，置n=1.

Step A2计算.更新路径流量，获得新的路径累积时间价值

Step A3方向搜索.基于，执行0-1加载，得到新的路段流量，下降方向为.

Step A4MSA移动.以步长为移动，获得.

Step A5检查收敛性.计算，取后3次的路段平均流量构造收敛判断函数.en≤ε时，算法终止；否则，转StepA6.

Step A6迭代次数判断.迭代次数n＞Nmax时，算法终止；否则，转StepA2，置n=n+1.

Stage BFrank-Walfe法求SO均衡解.

Step B1初始化.Stage A中不同风险态度下的最优流量分布xa(min(TEρ)),ρ∈[0,1]为初始路段流量，目标函数为,a∈A.令n=0，转Step B2.

Step B2方向搜索.求解ma∈iAn ∇f(xn)Tx，获得新的路段流量，下降方向为，置n=1.

Step B3检查收敛性.计算en= | ∇f(xn)T(yn-xn)|,en≤ε时，算法终止；否则，转Step B4.

Step B4迭代次数判断.迭代次数n＞Nmax时，算法终止；否则，转Step B5.

Step B6计算步长.求解获得下降步长λn，令xn+1=xn+λn(yn-xn),n=n+1，转Step B2.

4 数值算例

下面采用本文提出的连续风险态度双参考点网络均衡模型对Nguyen&Dupuis路网进行分析.如图2所示，全网共9个节点，19个路段，4个OD对(1-2、1-3、4-2、4-3)，OD需求矩阵为，路段时间模型采用随机退化BPR模型，参数为

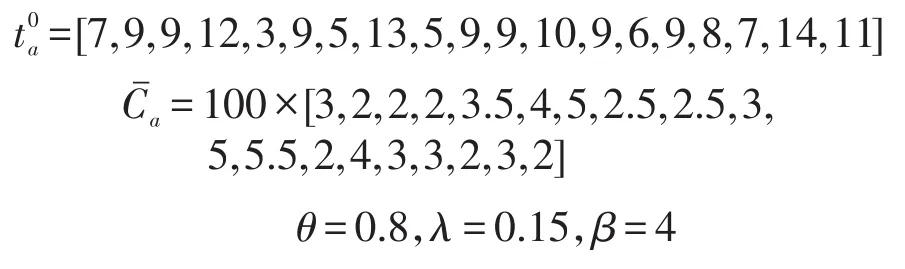
在设置参考点求解CPV时，相关参数有：ρ=0.8,ϕ=0.045,ϑ=[0.69,0.69,0.74,0.74],τ=[-2.250 0,1.000 0,2.538 9,-5.712 5]，α=[0.52,0.52,0.52,0.52].确定参考点时，相关参数有：γ=1.5，Tdepart=0，Twork=222.模型内生重要参数包括路段出行时间期望与标准差、路径最佳到达时间参考点、路径最早正效用时间参考点、路径CPV、用户均衡和系统最优均衡时的路段流量分布与路径流量分布，以及不同风险态度下的系统效率值.

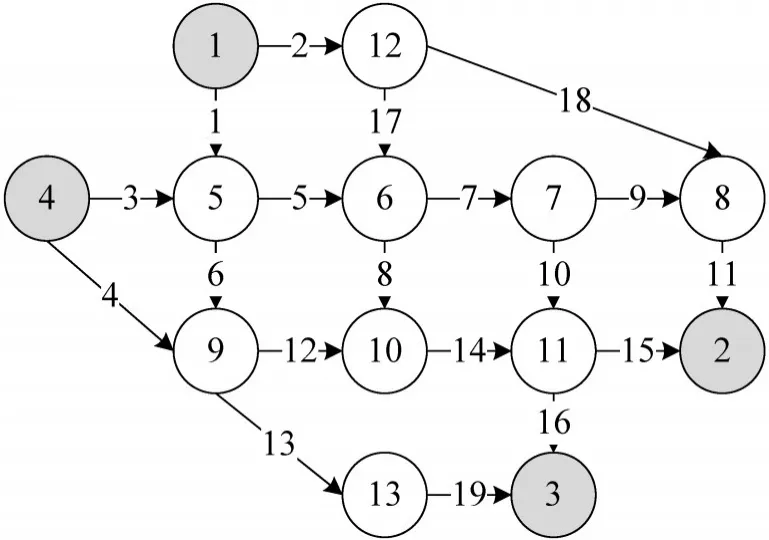
图2 Nguyen&Dupuis路网图Fig.2 Nguyen&Dupuis road network

经深度优先搜索获得4个OD对可行路径共25条，如表1所示.

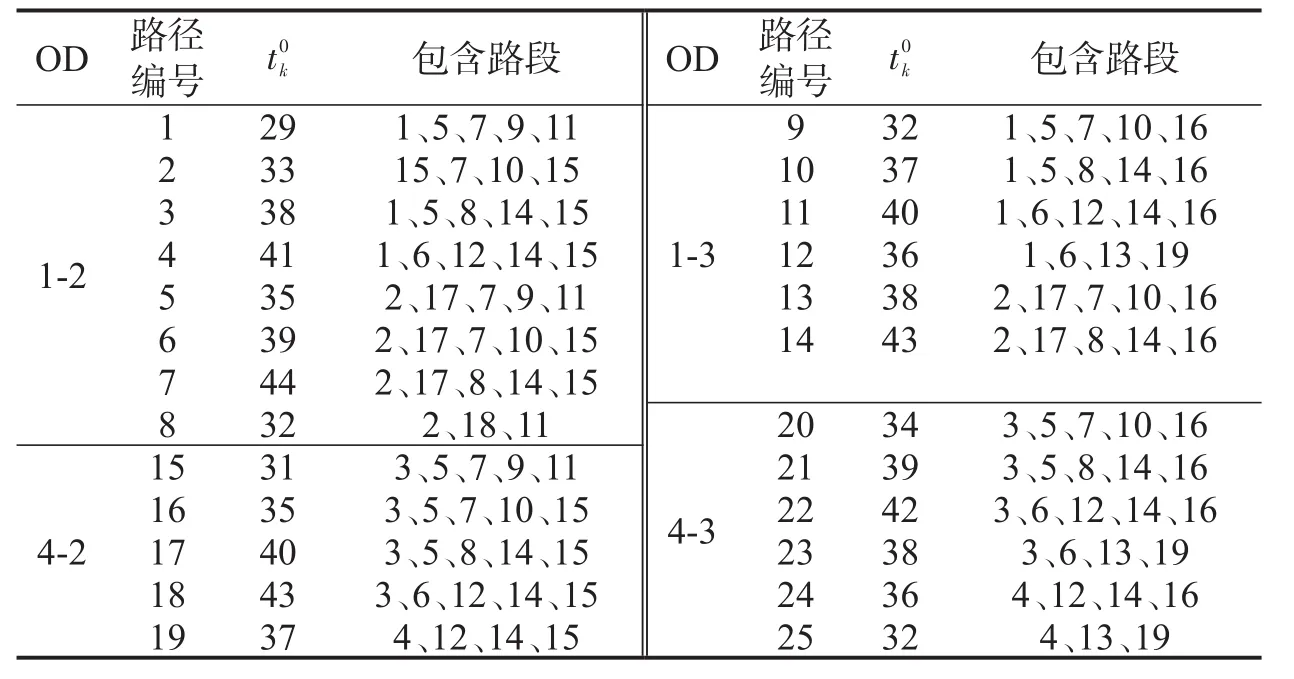
表1 OD对可行路径Table 1 Paths between 4 OD pairs

4.1 CPV_UE与SO均衡下的流量分布

图3和表2展示了CPV_UE与SO均衡下的系统流量分布状况.由图3可知，随着用户不迟到的概率最低要求σ逐渐增加，4个OD对间路径流量分布趋于平均.σ接近0点时，OD对1-2、1-3、4-2和4-3间绝大多数流量分别集中于路径8、路径9、路径15和路径25.

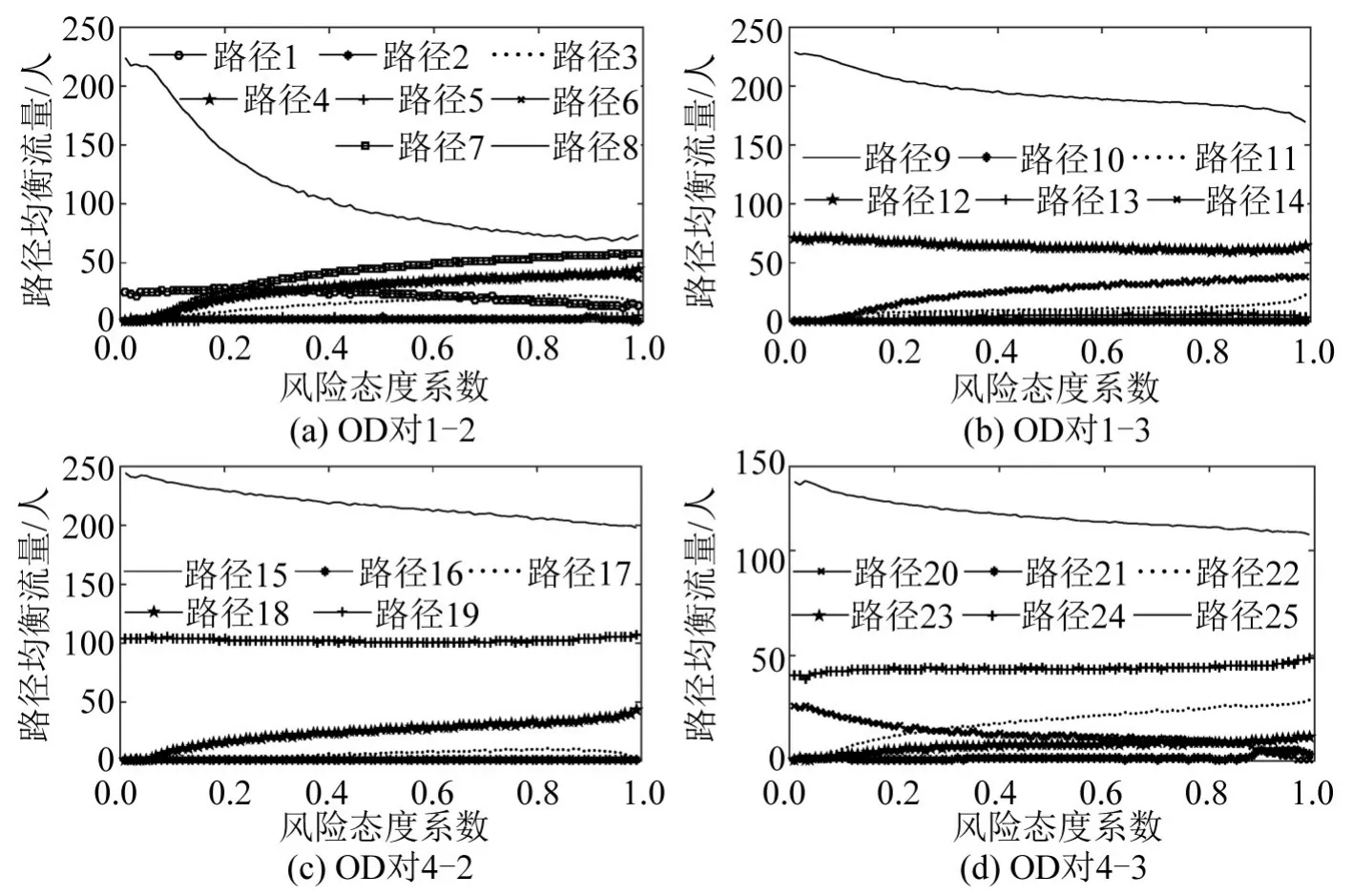
图3 不同风险态度下的UE均衡流量分布Fig.3 UE flow distribution with different risk attitude

由表2可知，当σ取不同值时，CPV_UE与SO均衡下的路径流量分布不同，SO均衡流量分布的集中程度，介于CPV_UE均衡模型在σ取0.01～0.50之间.

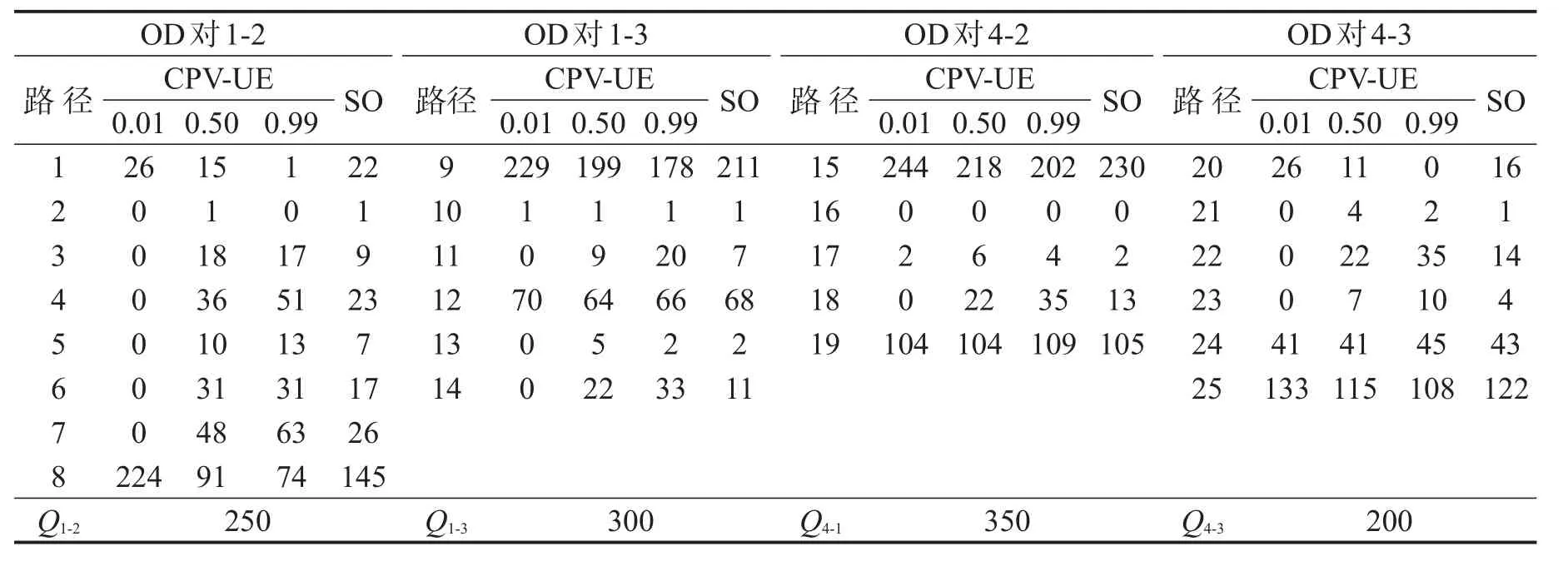
表2 CPV_UE与SO均衡流量分布Table 2 Flow distribution in CPV_UE and SO network

4.2 用户风险态度对系统效率的影响

图4展示了σ取不同值时，CPV_UE与SO均衡时的系统效率.随着σ的增加，CPV_UE系统I区平均宽度逐渐上升，III区平均宽度逐渐下降，II区平均宽度基本不变.这是由于随着用户不迟到的概率最低要求σ逐渐增加，用户预留出行时间上升，使得最佳到达时间参考点Tstar逐渐接近Twork.同时，由于早到收益区存在上限，II区宽度在超过上限后维持稳定宽度，进而令Tearly逐渐接近Twork，导致I区宽度增加.

随着用户不迟到的概率最低要求σ逐渐增加，正效用区间逐渐窄化，而负效用I区变宽.由于路网出行时间客观随机性来自其能力随机退化，与到达时间感知效用区间宽度无关.因此，随着σ的增加，TPV逐渐下降.这也解释了现实中虽然保守的用户更加倾向风险规避，但其到达时间感知价值却更低的特点.

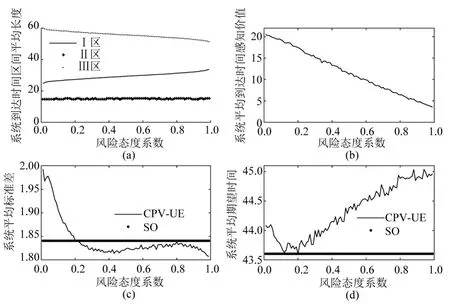
图4 ρ对系统效率的影响Fig.4 System efficiency with deferentρ

图4下半部分展示了CPV_UE和SO系统的TSD和TE值.随着σ的增加，TECPV_UE在σ≈0.2时存在拐点，此时TECPV_UE=min(TECPV_UE)，TESO≈min(TECPV_UE).与此同时，TSDCPV_UE震荡下降，并可分为3个区间：σ∈(0.0,0.3)时，TSDCPV_UE迅速下降；σ∈[0.3,0.8)时，TSDCPV_UE在震荡中趋于稳定；σ∈[0.8,1.0)时 ，TSDCPV_UE又一次迅速下降.TSDSO≈TSDCPV_UE(ρ=0.2,0.8).可见在随机能力退化的路网中，系统达到总期望时间最短时，其标准差大于绝大多数的TSDCPT_UE，说明管理者不能非常有效地掌控系统出行时间；当系统总期望时间最小时，由于存在较大标准差，整个系统出行时间依然存在较大的不确定性.而用户分散决策时，UE系统的不确定性显著小于SO系统.

5 结论

本文将双参考点CPV模型和随机能力退化路网模型相结合，从外部客观随机性(随机能力退化路网)和个体主观随机性(双参考点CPV)两个方面对交通网络均衡流量和均衡时间进行了定义、划分与分析，并提出了相应的系统效率分析模型.在此基础上，设计了基于MSA和Frank-walfe法的嵌套算法，求解本文提出的CPV_UE模型和经典SO模型.最后以Nguyen&Dupuis路网为例，对模型进行了试算并分析了系统效率.发现随着用户不迟到的概率最低要求σ逐渐增加，4个OD间的路径流量均衡分布趋于分散，到达时间晚到正区间宽度缩小，早到负区间宽度增加，用户获得的CPV下降，印证了保守用户在网络均衡时感受到的价值更低的特点，也发现保守用户群体在均衡时流量分布更分散.与此同时以σ=0.2为界，CPV_UE系统平均出行时间标准差先迅速下降，再维持稳定，系统平均期望时间先降后升.而SO均衡时，虽然系统平均期望时间最短，但其标准差在80%以上的情况下大于CPV_UE均衡.意味着在一个存在外部客观随机性(随机能力退化)的路网中，管理者即使通过各种手段能够促使整个系统获得期望时间最低，但仍不能进一步减少标准差，系统行程时间不确定性较大.从风险态度全区间来看，当用户风险系数大于0.2时CPV_UE均衡时系统不确定性相对SO均衡较低.